Вариант 7.

1. Вычислить неопределенные интегралы:

а) ; б) .

2. Вычислить определенный интеграл:

.

3. Вычислить методом трапеций с шагом интегрирования 0,1 приближенное значение определенного интеграла .

4. Найти общее решение дифференциального уравнения

e^y (1+x²) dy – 2x (1+ e^y) dx = 0.

5. Найти общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами у ^// + 3у ^/ = 0.

6. Исследовать ряд на абсолютную и условную сходимость.

7. Найти радиус сходимости степенного ряда .

Вариант 8.

1. Вычислить неопределенные интегралы:

а) ; б) .

2. Вычислить определенный интеграл:

.

3. Вычислить методом трапеций с шагом интегрирования 0,1 приближенное значение определенного интеграла .

4. Найти общее решение дифференциального уравнения

х² y^/. + y = 0 .

5. Найти общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами у ^// + 4у ^/ + 5у=0.

6. Исследовать ряд на абсолютную и условную сходимость.

7. Найти радиус сходимости степенного ряда .

Вариант 9.

1. Вычислить неопределенные интегралы:

а) ; б) .

2. Вычислить определенный интеграл:

.

3. Вычислить методом трапеций с шагом интегрирования 0,1 приближенное значение определенного интеграла .

4. Найти общее решение дифференциального уравнения

(xy²+x) dx + (y– x²y) dy = 0.

5. Найти общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами у ^// + у ^/ – 2y= 0.

6. Исследовать ряд на абсолютную и условную сходимость.

7. Найти радиус сходимости степенного ряда .

Вариант 10.

1. Вычислить неопределенные интегралы:

а) ; б) .

.

2. Вычислить определенный интеграл:

.

3. Вычислить методом трапеций с шагом интегрирования 0,1 приближенное значение определенного интеграла .

4. Найти общее решение дифференциального уравнения

(2y+1) x dx + (1+x² ) dy = 0.

5. Найти общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами у ^// - 2у ^/ = 0.

6. Исследовать ряд на абсолютную и условную сходимость.

7. Найти радиус сходимости степенного ряда .

Методические указания к контрольной работе № 2

Ниже приведены образцы решения отдельных задач.

1. Вычислить неопределенные интегралы:

а) .

Решение

а) Преобразуем подынтегральную функцию

.

б)

Решение

б) Обозначим t = x³ – 1 , тогда x³ = t+1 , откуда

; .

Подставляя в интеграл, получим

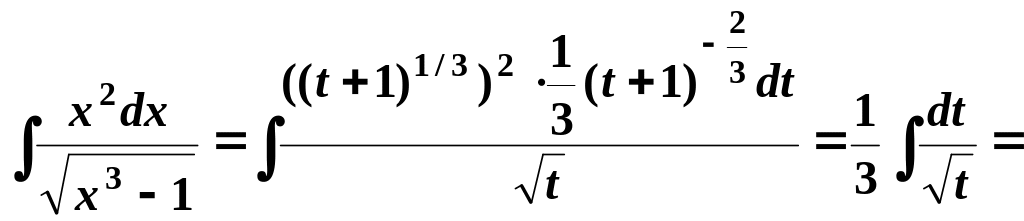
2. Вычислить определенный интеграл:

.

Воспользуемся формулой Ньютона-Лейбница: eсли F(x) – первообразная для f(x), то

Тогда

= 3(1/2 – 0) + 3(1 – 0) + 2 ^{– 1} – 1 ^{– 1} = 3/2 + 3 + 1/2 – 1 = 4 .

3. Вычислить методом трапеций с шагом интегрирования 0,1 приближенное значение определенного интеграла .

Решение. Разобьем отрезок интегрирования на n = 10 частей и вычислим с точностью до 0,001 значения подынтегральной функции в точках разбиения. Получим

x	0,0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0
f(x)	0,540	0,549	0,574	0,614	0,667	0,732	0,802	0,873	0,936	0,982	1,000

Формула для вычисления приближенного значения определенного интеграла методом трапеций имеет вид

, где

Выполнив вычисления по этой формуле, получим в результате 0,7499. Округлив результат до двух знаков после запятой, получим значение 0,75.

Ответ. Приближенное значение интеграла равно 0,75.