Пример: По заданной логической схеме составить логи­ческое выражение и заполнить для него таблицу истинности

Решение: Во-первых, определяем, сколько входов име­ется. Их в данной схеме три. Обозначаем их символами, на­пример: x, y, z. Во-вторых, смотрим, какие логические эле­менты составляют схему и аккуратно изображаем эти эле­менты в виде формул. Получаем следующее логическое выра­жение: .

Составляем таблицу истинности. Т.к. имеется три входа, то будет 2³=8 различных логических комбинаций 1 и 0.

(Заметим, что необходимо не забывать об инвертировании вы­ражений)

x	y	z
0	0	0	0	1	0	1	1	0	1	1
0	0	1	1	0	0	0	0	0	1	1
0	1	0	1	0	0	1	1	1	0	0
0	1	1	1	0	0	0	0	0	1	1
1	0	0	0	1	1	1	1	0	1	1
1	0	1	1	0	0	0	1	0	1	1
1	1	0	1	0	0	1	1	1	0	0
1	1	1	1	0	0	0	1	1	0	0

Задачи:

1. По заданному логическому выражению построить таблицу истинности и составить логическую схему.

а)

б)

в)

г)

д)

е)

ж)

2. По заданной логической схеме составить логическое выра­жение и заполнить для него таблицу истинности.

а )	б )
в )	г )
д )	е )

2.2 Основные соотношения алгебры логики

При решении логических задач и построении схем часто приходится упрощать формулы, полученные при форма­лизации их условий. Упрощение формул в алгебре логики производится на основе эквивалентных преобразований, опи­рающихся на основные логические законы.

1. Аксиома 1:

2. Аксиома 2:

3. Аксиома 3:

4. Аксиома 4:

5. Закон исключенного третьего: (В один и тот же момент времени высказывание может быть или истинным или ложным, третьего не дано.)

6. Закон противоречия: (Высказывание не может быть истинным и ложным одновременно. Например: вы­ключатель не может быть включенным и выключенным одновременно)

7. Закон двойного отрицания: (Например: пусть х = 1, тогда , и следовательно )

8. Законы коммутативности: (переместительные)

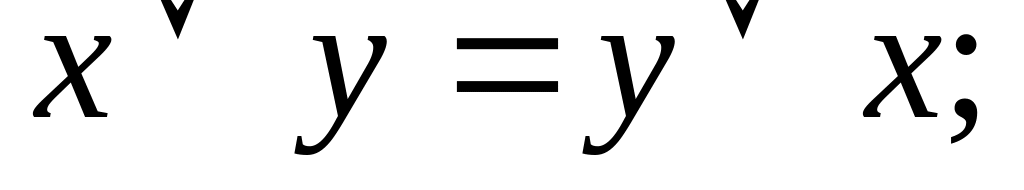
9. Законы ассоциативности: (сочетательные) ;

10. Законы де Моргана: (отрицание вариантов вместе); (отрицание одновременной истинно­сти)

11. Законы дистрибутивности:

12. Законы поглощения: ;

13. Законы склеивания: ;

Под упрощением формулы, не содержащей операций импликации и эквиваленции, понимают равносильное преоб­разование, приводящее к формуле, которая либо содержит по сравнению с исходной меньшее количество операций конъ­юнкции и дизъюнкции и не содержит отрицаний неэлементар­ных формул, либо содержит меньшее число вхождений пере­менных.

Пример: Упростить логическое выражение

1.

2.

Задачи:

Упростить заданное логическое выражение

1.

2.

3.

4.

5.

Лабораторная работа №2

Логические основы ЭВМ

ВАРИАНТ 1

1. По заданному логическому выражению составить логиче­скую схему и построить таблицу истинности

а) б)

2. По заданной логической схеме составить логическое вы­ражение и заполнить для него таблицу истинности

   а)

   б)

3. Упростить заданное логическое выражение

а) б)

ВАРИАНТ 2

1. По заданному логическому выражению составить логиче­скую схему и построить таблицу истинности

а) б)

2. По заданной логической схеме составить логическое выра­жение и заполнить для него таблицу истинности

   а)

   б)

3. Упростить заданное логическое выражение:

ВАРИАНТ 3

1. По заданному логическому выражению составить логиче­скую схему и построить таблицу истинности

а) б)

2. По заданной логической схеме составить логическое выра­жение и заполнить для него таблицу истинности

а)

б)

3. Упростить заданное логическое выражение:

ВАРИАНТ 4

1. По заданному логическому выражению составить логиче­скую схему и построить таблицу истинности

а) б)

2. По заданной логической схеме составить логическое выра­жение и заполнить для него таблицу истинности

   а)

   б)

3. Упростить заданное логическое выражение:

ВАРИАНТ 5

1. По заданному логическому выражению составить логиче­скую схему и построить таблицу истинности

а) б)

2. По заданной логической схеме составить логическое выра­жение и заполнить для него таблицу истинности

   а)

   б)

3. Упростить заданное логическое выражение:

ВАРИАНТ 6

1. По заданному логическому выражению составить логиче­скую схему и построить таблицу истинности

а) б)

2. По заданной логической схеме составить логическое выра­жение и заполнить для него таблицу истинности

   а)

   б)

3. Упростить заданное логическое выражение:

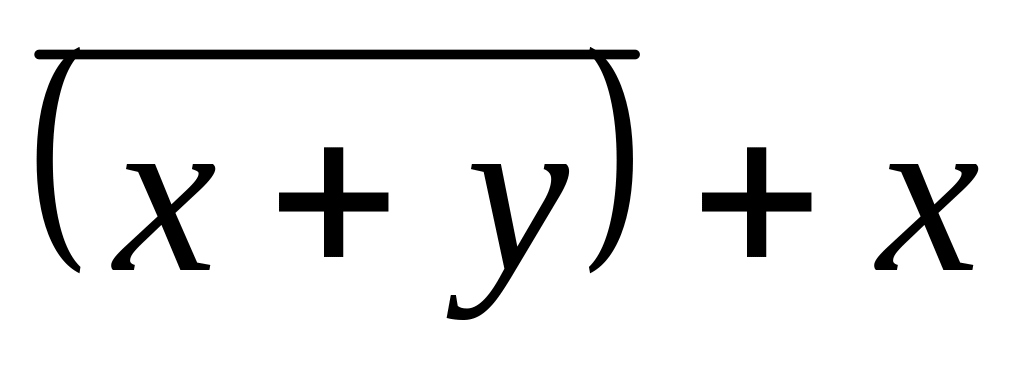
ВАРИАНТ 7

1. По заданному логическому выражению составить логиче­скую схему и построить таблицу истинности

а) б)

2. По заданной логической схеме составить логическое выра­жение и заполнить для него таблицу истинности

   а)

   б)

3. Упростить заданное логическое выражение:

ВАРИАНТ 8

1. По заданному логическому выражению составить логиче­скую схему и построить таблицу истинности

а) б)

2. По заданной логической схеме составить логическое выра­жение и заполнить для него таблицу истинности

   а)

   б)

3. Упростить заданное логическое выражение:

ВАРИАНТ 9

1. По заданному логическому выражению составить логиче­скую схему и построить таблицу истинности

а) б)

2. По заданной логической схеме составить логическое выра­жение и заполнить для него таблицу истинности

   а)

   б)

3. Упростить заданное логическое выражение:

ВАРИАНТ 10

1. По заданному логическому выражению составить логиче­скую схему и построить таблицу истинности

а) б)

2. По заданной логической схеме составить логическое выра­жение и заполнить для него таблицу истинности

   а)

   б)

3. Упростить заданное логическое выражение:

ВАРИАНТ 11

1. По заданному логическому выражению составить логиче­скую схему и построить таблицу истинности

а) б)

2. По заданной логической схеме составить логическое выра­жение и заполнить для него таблицу истинности

   а)

   б)

3. Упростить заданное логическое выражение:

ВАРИАНТ 12

1. По заданному логическому выражению составить логиче­скую схему и построить таблицу истинности

а) б)

2. По заданной логической схеме составить логическое выра­жение и заполнить для него таблицу истинности

   а)

   б)

3. Упростить заданное логическое выражение:

ВАРИАНТ 13

1. По заданному логическому выражению составить логиче­скую схему и построить таблицу истинности

а) б)

2. По заданной логической схеме составить логическое выра­жение и заполнить для него таблицу истинности

   а)

   б)

3. Упростить заданное логическое выражение:

ВАРИАНТ 14

1. По заданному логическому выражению составить логиче­скую схему и построить таблицу истинности

а) б)

2. По заданной логической схеме составить логическое выра­жение и заполнить для него таблицу истинности

   а)

   б)

3. Упростить заданное логическое выражение:

ВАРИАНТ 15

1. По заданному логическому выражению составить логиче­скую схему и построить таблицу истинности

а) б)

2. По заданной логической схеме составить логическое выра­жение и заполнить для него таблицу истинности

   а)

   б)

3. Упростить заданное логическое выражение:

ВАРИАНТ 16

1. По заданному логическому выражению составить логиче­скую схему и построить таблицу истинности

а) б)

2. По заданной логической схеме составить логическое выра­жение и заполнить для него таблицу истинности

   а)

   б)

3. Упростить заданное логическое выражение:

ВАРИАНТ 17

1. По заданному логическому выражению составить логиче­скую схему и построить таблицу истинности

а) б)

2. По заданной логической схеме составить логическое выра­жение и заполнить для него таблицу истинности

   а)

   б)

3. Упростить заданное логическое выражение:

ВАРИАНТ 18

1. По заданному логическому выражению составить логиче­скую схему и построить таблицу истинности

а) б)

2. По заданной логической схеме составить логическое выра­жение и заполнить для него таблицу истинности

   а)

   б)

3. Упростить заданное логическое выражение: