6. Двухвыборочный f-тест для дисперсий

   1. Этот инструмент реализует критерии Фишера проверки равенства дисперсий двух независимых выборок из нормально распределенных генеральных совокупностей с дисперсиями σ1 и σ2, соответственно.

   2. Вызовите инструмент создания выборки через Данные> Анализ данных> Двухвыборочный F-тест для дисперсий.

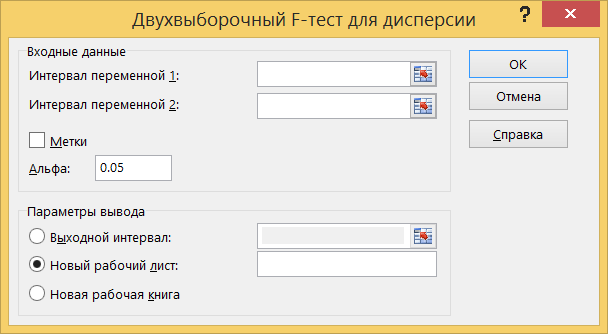
3. Параметры инструмента. В поле Интервал переменной 1 задается адрес диапазона ячеек, содержащий выборку с большим математическим ожиданием. В поле Интервал переменной 2 указывается адрес второй выборки. В поле Альфа вводится значение уровня значимости. Выходной интервал – область вывода рассчитанных данных.. В поле Альфа вводится значение уровня значимости α.

4. Заполните параметры в соответствии с рисунком. Проверьте, что в поле Входной интервал 1 задана выборка, имеющая большую дисперсию. Нажмите OK.

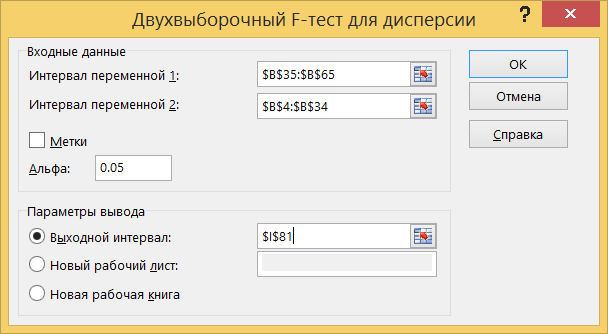
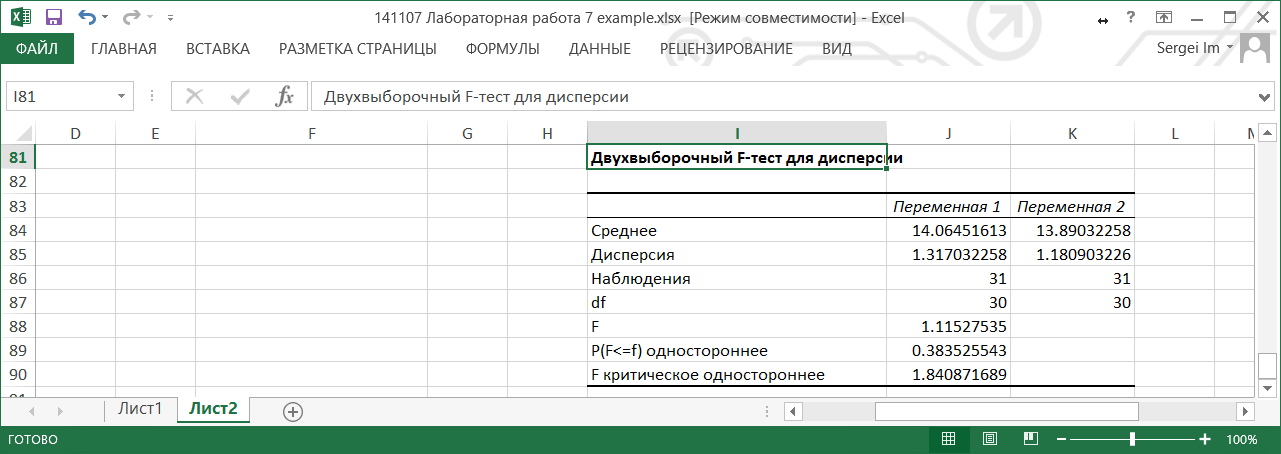
5. В итоговой таблице представлены следующие данные

Таким образом, дисперсии анализируемых выборок статистически не различаются при уровне значимости 0.05.

6. Расчет корреляций

   1. Корреляционный анализ используется для количественной оценки взаимосвязи двух наборов данных, представленных в безразмерном виде. Выборочный коэффициент линейной корреляции вычисляется по формуле 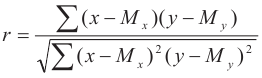, где x и y – значения из выборок, M – средние арифметические. Если большие значения из одного набора данных связаны с большими значениями другого набора, то корреляция положительна, если малые значения одного набора связаны с большими значениями другого, то корреляция отрицательна, если данные двух диапазонов никак не связаны между собой, корреляция близка к нулю.

2. Выделите ячейку С1. Вставьте два дополнительных столбца через Главная> Вставить> Вставить столбцы на лист.

3. С листа 1 скопируйте колонки значений из соседних столбцов относительно вашего выбранного варианта.

4. Вызовите инструмент создания выборки через Данные> Анализ данных> Корреляции.

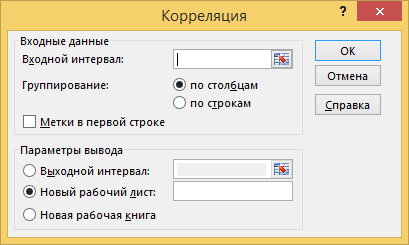
5. Укажите параметры как на рисунке. Нажмите OK.

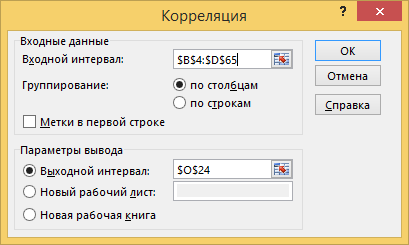
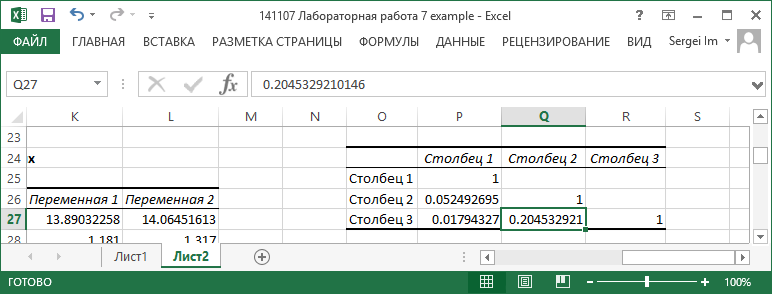
6. В данном примере коэффициенты линейной корреляции низкие.

1. Вычисление линейной регрессии

   1. Линейный регрессионный анализ заключается в подборе графика для набора наблюдений с помощью метода наименьших квадратов. Регрессионный анализ позволяет установить функциональную зависимость между некоторой случайной величиной Y и некоторыми влияющими на Y величинами X. Такая зависимость получила название уравнения регрессии. Различают простую (y=m*x+b) и множественную (y=m₁*x₁+m₂*x₂+... + m_k*x_k+b) регрессию линейного и нелинейного типа. Для оценки степени связи между величинами используется коэффициент множественной корреляции R Пирсона (корреляционное отношение), который может принимать значения от 0 до 1. R=0, если между величинами нет никакой связи, и R=1, если между величинами имеется функциональная связь. В большинстве случаев R принимает промежуточные значения от 0 до 1. Величина R² называется коэффициентом детерминации. Задачей построения регрессионной зависимости является нахождение вектора коэффициентов M модели множественной линейной регрессии, при котором коэффициент R принимает максимальное значение. Для оценки значимости R применяется F-критерий Фишера, вычисляемый по формуле: 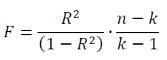где n – количество экспериментов; k – число коэффициентов модели. Если F превышает некоторое критическое значение для данных n и k и принятой доверительной вероятности, то величина R считается существенной.

   2. Инструмент Регрессия из Пакета анализа позволяет вычислить следующие данные:

• коэффициенты линейной функции регрессии – методом наименьших квадратов; вид функции регрессии определяется структурой исходных данных;

• коэффициент детерминации и связанные с ним величины (таблица Регрессионная статистика);

• дисперсионную таблицу и критериальную статистику для проверки значимости регрессии (таблица Дисперсионный анализ);

• среднеквадратическое отклонение и другие его статистические характеристики для каждого коэффициента регрессии, позволяющие проверить значимость этого коэффициента и построить для него доверительные интервалы;

• значения функции регрессии и остатки – разности между исходными значениями переменной Y и вычисленными значениями функции регрессии (таблица Вывод остатка);

• вероятности, соответствующие упорядоченным по возрастанию значениям переменной Y (таблица Вывод вероятности).

3. Вызовите инструмент создания выборки через Данные> Анализ данных> Регрессия.

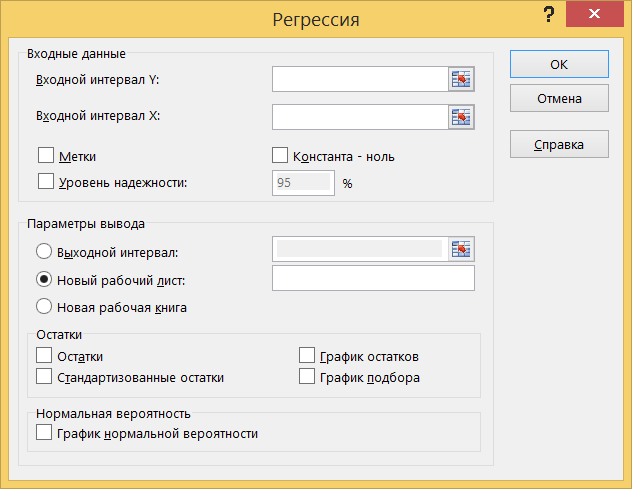
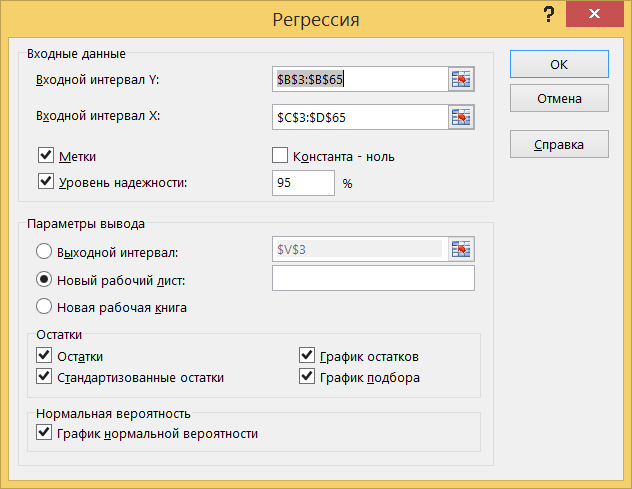
4. В поле Входной интервал Y вводится адрес диапазона, содержащего значения зависимой переменной Y. Диапазон должен состоять из одного столбца. В поле Входной интервал X вводится адрес диапазона, содержащего значения переменной X. Диапазон должен состоять из одного или нескольких столбцов, но не более чем из 16 столбцов. Если указанные в полях Входной интервал Y и Входной интервал X диапазоны включают заголовки столбцов, то необходимо установить флажок опции Метки – эти заголовки будут использованы в выходных таблицах, сгенерированных инструментом Регрессия. Флажок опции Константа - ноль следует установить, если в уравнении регрессии константа b принудительно полагается равной нулю. Опция Уровень надежности устанавливается тогда, когда необходимо построить доверительные интервалы для коэффициентов регрессии с доверительным уровнем, отличным от 0.95, который используется по умолчанию. После установки флажка опции Уровень надежности становится доступным поле ввода, в котором вводится новое значение доверительного уровня. В области Остатки имеются четыре опции: Остатки, Стандартизованные остатки, График остатков и График подбора. Если установлена хотя бы одна из них, то в выходных результатах появится таблица Вывод остатка, в которой будут выведены значения функции регрессии и остатки – разности между исходными значениями переменной Y и вычисленными значениями функции регрессии. В области Нормальная вероятность имеется одна опция – График нормальной вероятности; ее установка порождает в выходных результатах таблицу Вывод вероятности и приводит к построению соответствующего графика.

5. Установите параметры в соответствии с рисунком. Проверьте, что в качестве величины Y указана первая переменная (включая ячейку с названием), и в качестве величины X указаны две остальные переменные (включая ячейки с названиями). Нажмите OK.

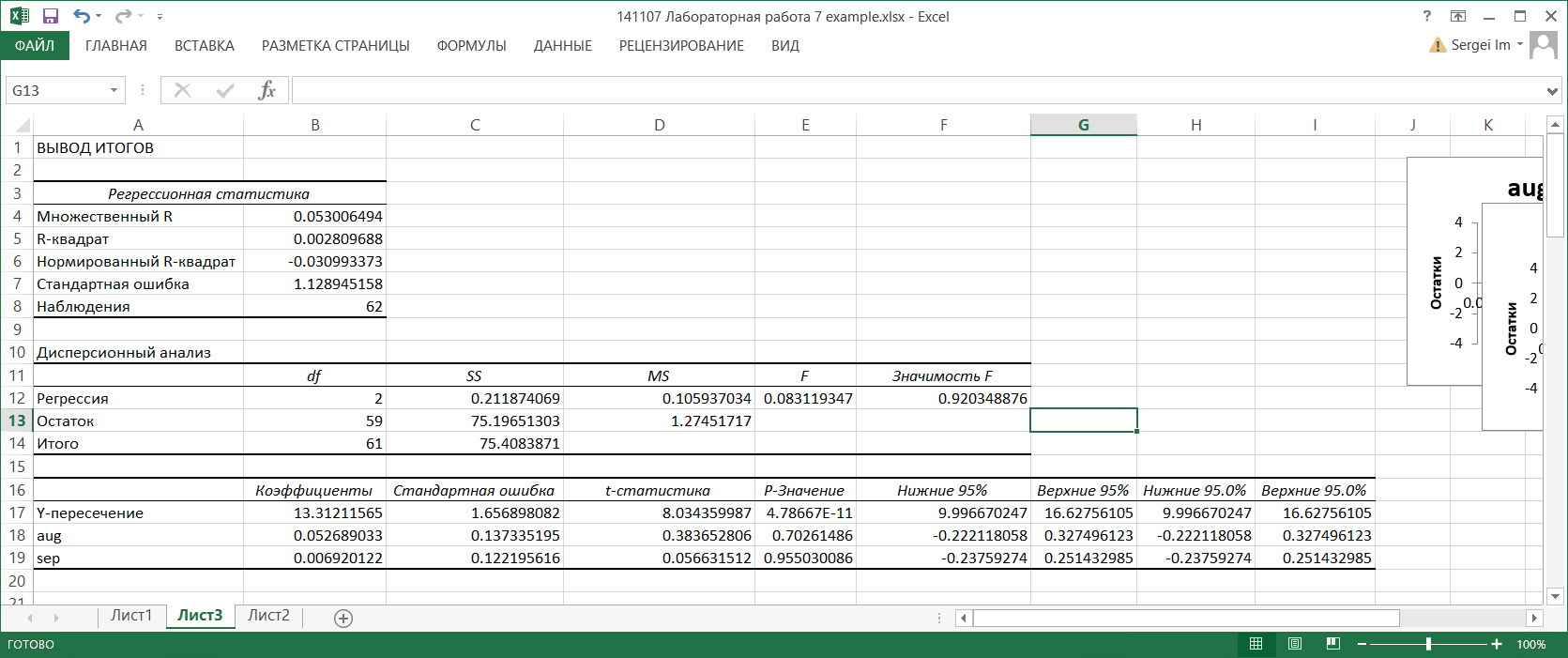
6. В таблице Регрессионная статистика приводятся следующие данные.

Множественный R – корень из коэффициента детерминации R², приведенного в следующей строке. Другое название этого показателя – индекс корреляции, или множественный коэффициент корреляции.

R-квадрат – коэффициент детерминации R²; вычисляется как отношение регрессионной суммы квадратов (ячейка С12) к полной сумме квадратов (ячейка С14).

Нормированный R-квадрат вычисляется по формуле

где n – количество значений переменной Y, k – количество столбцов во входном интервале переменной X.

Стандартная ошибка – корень из остаточной дисперсии (ячейка D13).

Наблюдения – количество значений переменной Y.

7. В Дисперсионной таблице в столбце SS приводятся суммы квадратов, в столбце df – число степеней свободы. в столбце MS – дисперсии. В строке Регрессия в столбце f вычислено значение критериальной статистики для проверки значимости регрессии. Это значение вычисляется как отношение регрессионной дисперсии к остаточной (ячейки D12 и D13). В столбце Значимость F вычисляется вероятность полученного значения критериальной статистики. Если эта вероятность меньше, например, 0.05 (заданного уровня значимости), то гипотеза о незначимости регрессии (т.е. гипотеза о том, что все коэффициенты функции регрессии равны нулю) отвергается и считается, что регрессия значима. В данном примере регрессия незначима.

8. В следующей таблице, в столбце Коэффициенты, записаны вычисленные значения коэффициентов функции регрессии, при этом в строке Y-пересечение записано значение свободного члена b. В столбце Стандартная ошибка вычислены среднеквадратические отклонения коэффициентов. В столбце t-статистика записаны отношения значений коэффициентов к их среднеквадратическим отклонениям. Это значения критериальных статистик для проверки гипотез о значимости коэффициентов регрессии. В столбце P-Значение вычисляются уровни значимости, соответствующие значениям критериальных статистик. Если вычисленный уровень значимости меньше заданного уровня значимости (например, 0.05). то принимается гипотеза о значимом отличии коэффициента от нуля; в противном случае принимается гипотеза о незначимом отличии коэффициента от нуля. В данном примере только коэффициент b значимо отличается от нуля, остальные – незначимо. В столбцах Нижние 95% и Верхние 95% приводятся границы доверительных интервалов с доверительным уровнем 0.95. Эти границы вычисляются по формулам Нижние 95% = Коэффициент - Стандартная ошибка * t_α; Верхние 95% = Коэффициент + Стандартная ошибка * t_α. Здесь t_α – квантиль порядка α распределения Стьюдента с (n-k-1) степенью свободы. В данном случае α = 0.95. Аналогично вычисляются границы доверительных интервалов в столбцах Нижние 90.0% и Верхние 90.0%.

9. Рассмотрим таблицу Вывод остатка из выходных результатов. Эта таблица появляется в выходных результатах только тогда, когда установлена хотя бы одна опция в области Остатки диалогового окна Регрессия.

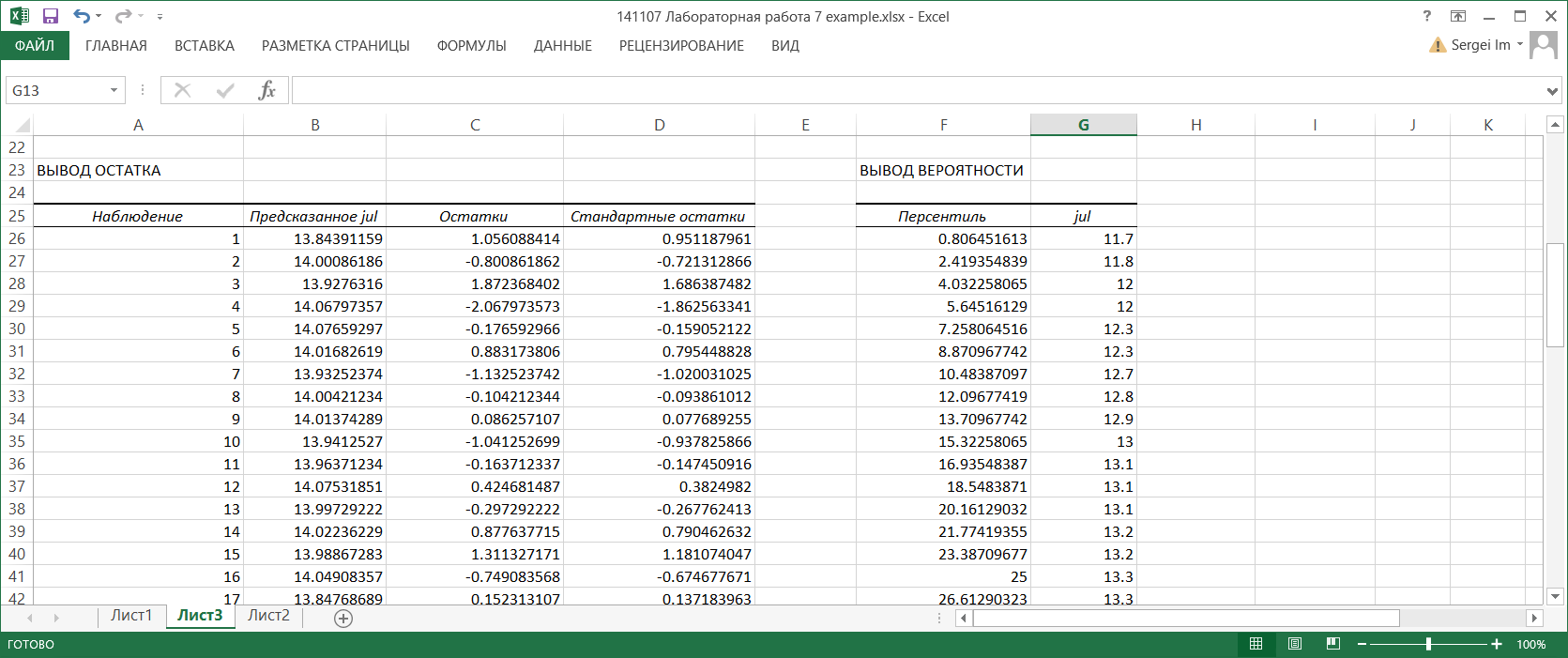
В столбце Наблюдение приводятся порядковые номера значений переменной Y. В столбце Предсказанное Y вычисляются значения функции регрессии у_i = f(х_i) для тех значений переменной X, которым соответствует порядковый номер i в столбце Наблюдение. В столбце Остатки содержатся разности (остатки) ε_i=Y-у_i , а в столбце Стандартные остатки – нормированные остатки, которые вычисляются как отношения ε_i / s_ε. где s_ε – среднеквадратическое отклонение остатков. Квадрат величины s_ε вычисляется по формуле

где – среднее остатков. Величину можно вычислить как отношение двух значений из дисперсионной таблицы: суммы квадратов остатков (ячейка С13) и степени свободы из строки Итого (ячейка В14).

10. По значениям таблицы Вывод остатка строятся два типа графиков: графики остатков и графики подбора (если установлены соответствующие опции в области Остатки диалогового окна Регрессия). Они строятся для каждого компонента переменной X в отдельности.

На графиках остатков отображаются остатки, т.е. разности между исходными значениями Y и вычисленными по функции регрессии для каждого значения компонента переменной X.

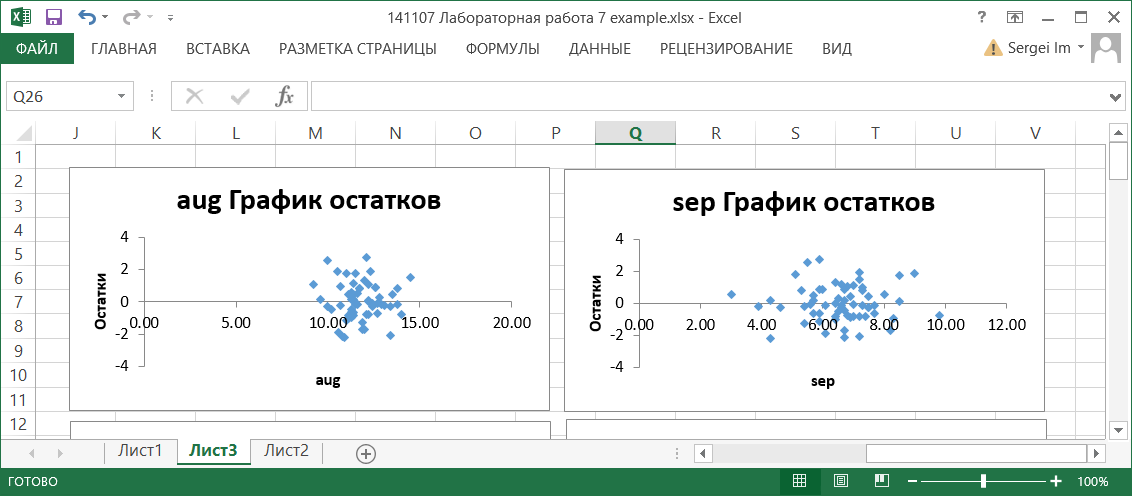
На графиках подбора отображаются как исходные значения Y, так и вычисленные значения функции регрессии для каждого значения компонента переменной X.