19

РЕФЕРАТ

Сторінок 37, рисунків 10, таблиць 22, посилань 4

У курсовому проекті розглянутий абстрактний цифровий автомат Мілі заданого пристрою, алгоритм його роботи, складений граф автомата Мілі, таблиці збудження пам’яті, складені функції збудження, складена функціональна і електрична принципова схеми.

Також виконано проектування лічильника з коефіцієнтом перерахунку К=13, таблиця його функціональності, побудована структурна схема лічильника.

АВТОМАТ МИЛІ, ГРАФ, ТАБЛИЦЯ ІСТИННОСТІ, ТАБЛИЦЯ ПЕРЕХОДІВ-ВИХОДІВ, ТРИГЕРИ, КОДУВАННЯ, ФУНКЦІОНАЛЬНА СХЕМА, АРИФМЕТИКО-ЛОГІЧНИЙ ПРИСТРІЙ, ЕЛЕКТРИЧНА ПРИНЦИПОВА СХЕМА.

ЗМІСТ

Вступ…………………………………………………………………………….…5

1 Цифрові автомати…..…………………………………………………………...….....6

1. Основні поняття теорії автоматів.……………………….............…….…7

2. Етапи синтезу цифрових автоматів ………………………………......…..9

1.3 Додавання та віднімання у додатковому коді ……………….……..….10

2 Розробка арифметико-логічного пристрою, що виконує операції додавання та віднімання у зворотному двійковому коді………………………………….15

2.1 Завдання і вихідні дані…………………………………………………..15

2.2 Розробка алгоритму пристрою………………………………………… 15

2.3 Побудова абстрактного автомата Мілі (граф, таблиця переходів – виходів)……………………………………………………………………….…..19

2.4 Побудова функціональної схеми……….…….…….…….…….……....26

2.5 Побудова електричної принципової схеми арифметико-логічного пристрою ………….………..................................................................................28

3 Проектування КС………………………………………………………………30

3.1 Етапи синтезу лічильників………………………………………………30

3.2 Проектування лічильника на JK-тригерах з коефіцієнтом перерахунку К=13………………………………………………………………………………31

Висновки…………………………………………………...……….................…36

Перелік посилань………………………………………………………….……..37

ВСТУП

В сучасній науці і техніці одну з найважливіших ролей відіграють цифрові методи обробки інформації. В зв’язку з цим безперервно розширюється область використання цифрових систем – технічних засобів, виконуючих завершений процес обробки цифрової інформації, який включає її прийом, зберігання, необхідні перетворення і видачу.

Мікроелектроніка являється однією із найбільш швидко розвиваючих областей науки і техніки. Безперервно покращуються технічні характеристики і розширюються функціональні можливості мікроелектронних виробів. Саме мікроелектроніка сприяє розвитку цифрової техніки.

Логічні пристрої, працюючі з цифровим сигналом отримали широке застосування в електроніці. Стали розвиватися науки пов'язані з цифровими пристроями: "Цифрова схемотехніка", "Цифрові автомати".

Основою усіх цифрових пристроїв є прості логічні елементи, що виконують прості логічні операції алгебри-логіки. Усе більш складні цифрові пристрої можна представити у вигляді простих пристроїв - логічних елементів. Конструювання електронних схем і ефективне застосування цифрових пристроїв неможливе без уявлень про принципи їх дії і основниих параметрів.

Перетворення інформації, представленої в цифровому вигляді, здійснюється шляхом виконання певної послідовності арифметичних і логічних операцій. [1]

1 Цифрові автомати

Термін автомат, як правило, використовується в двох аспектах. З однією сторони, автомат — пристрій, що виконує деякі функції без безпосереднього участі людини. З іншого боку, термін «автомат» як математичне поняття позначає математичну модель реальних технічних автоматів. У цьому аспекті автомат представляється як «чорний ящик», що має кінцеве число входів і виходів і деяку безліч внутрішніх станів Q = [qi(t),dt(t) ... qn(t)], у яких він під впливом вхідних сигналів переходить стрибкоподібно, тобто практично миттєво, минувши проміжний стан. Звичайно, ця умова не виконується в реальності, оскільки будь-який перехідний процес триває певий час.

Цифрові автомати (ЦА) оперують з інформацією, представленою у вигляді цифрових (дискретних) значень фізичних величин. Будь-яке число реалізується комбінацією станів окремих фізичних елементів. Оскільки в ЦА в основному застосовується двійкова система числення, то як елементи використовуються найпростіші фізичні елементи, що володіють тільки двома стійкими станами. [1]

Точність представлення будь-якої математичної змінної в ЦА залежить тільки від вибраного числа розрядів двійкового коду, що принципово забезпечує високу точність рішення задач. Великою перевагою ЦА є те, що вони є алгоритмічно універсальні перетворювачі інформації з гнучким програмним управлінням і з повною автоматизацією рішення задачі. Ця обставина дозволяє використовувати ЦА для вирішення принципово будь-яких задач, що мають алгоритм рішення. Проте алгоритмічне рішення будь-якої задачі пов'язане з послідовністю виконання елементарних операцій, тому час рішення задач на ЦА залежить від кількості таких операцій і часу їх виконання, тобто у ряді випадків швидкодія ЦА може бути недостатньою для вирішення задач в реальному масштабі часу або при необхідності обробки великих масивів інформації.

Все різноманіття елементів, вузлів, блоків і пристроїв, з яких складається будь-який комп’ютер, є прикладом різних типів того або іншого ступеня складності перетворювачів цифрової інформації — цифрових автоматів. Методи теорії цифрових автоматів, що є математичною моделлю цифрових (дискретних) пристроїв, використовуються як теоретична база для аналізу і синтезу різних цифрових вузлів і пристроїв обчислювальних машин.

Оскільки, при вивченні цифрових автоматів мають справу з математичними моделями, то вживання основних положень теорії цифрових автоматів не обмежується конкретною областю, наприклад комп’ютером, а може бути використано для аналізу і синтезу різних автоматичних пристроїв в багатьох областях науки і техніки.

Під цифровим автоматом розуміється пристрій, призначений для перетворення цифрової (дискретної) інформації, здатний переходити під впливом вхідних сигналів з одного стану в інший і видавати вихідні сигнали

1. Основні поняття теорії автоматів

Автомат називається кінцевим, якщо безліч його внутрішніх станів і безліч значень вхідних сигналів — кінцева безліч. У практиці часто використовується поняття цифрового автомата, під яким розуміють пристрій, призначений для перетворення цифрової інформації. Вхідні сигнали в цифрових автоматах представляються у вигляді кінцевої безлічі миттєвих сигналів.

Цифровий автомат називається правильним, якщо вихідний сигнал в(t) визначається лише його станом q(t— 1) або q(t) і не залежить від вхідних сигналів. Поняття стану автомата використовується для опису систем, виходи яких залежать не лише від вхідних сигналів в даний момент часу, але і від сигналів, які поступили на входи системи раніше. Стан автомата відповідає деякій пам'яті про минуле, дозволяючи усунути час як явну змінну і виразити вихідні сигнали як функцію станів і вхідних сигналів.

Абстрактний автомат задається функцією переходів f, що визначає полягання автомата z(S+1) в S+1-м такті залежно від полягання автомата z(s) і значення вхідної букви х(S) в s-м-коді такті z(s+1} = f(z(S),х(S)) і функцією виходів, що визначає значення вихідної букви в(S) залежно від полягання автомата z(S) і вхідної букви х(S) в S -му такті в(S)= *(z(S),х(S))

За способом формування функції виходу виділяють автомат Милі і автомат Мура.

Автомат Милі: Автомат Мура:

y^(S) = (z^(S),х^(S)) y^(S) = (z^(S))

z^(s+1}= f(z^(S),х^(S)); z^(s+1}= f(z^(S),х^(S));

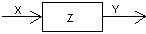
Рисунок 1.1 – Абстрактний автомат з одним входом і одним виходом

Функції (z(S),х(S)) і f(z(S),х(S)), що описують роботу автомата Милі, можна задати за допомогою таблиць переходів (табл.1.1) і виходів (табл.1.2). По цих таблицях можна визначити реакцію автомата на будь-яке вхідне слово.

Таблиця 1.1 – Таблиця переходів Таблиця 1.2– Таблиця виходів

	Z0	Z1	Z2	Z3			Z0	Z1	Z2	Z3
XI	Z1	Z2	Z0	Z3		X1	Уз	У2	У1	У1
Х2	Z3	Z2	Z0	Z0		Х2	У4	Уз	У4	У2
X3	Z2	Z1	Z2	Z3		X3	У1	У2	У4	У1

Функціонування автомата Мура задається однією таблицею (табл.1.3) переходів-виходів, при цьому в заголовку таблиці над станами автомата записуються вихідні сигнали, які автомат в цьому випадку формує.

Таблиця 1.3 – Таблиця переходів - виходів

	Y3 Z0	Y3 Z1	Y2 Z2	Y1 Z3	Y3 Z4
XI	Z2	Z2	Z4	Z4	Z1
X2	Z1	Z3	Z3	Z0	Z4

Граф автомата складається з вузлів (вершин) сполучених гілками (ребрами). Вузли графа ототожнюються із станами автомата, а гілки наголошуються вхідними сигналами, що викликають перехід автомата по даній гілці, і вихідними сигналами, відповідними такому переходу.

а) б)

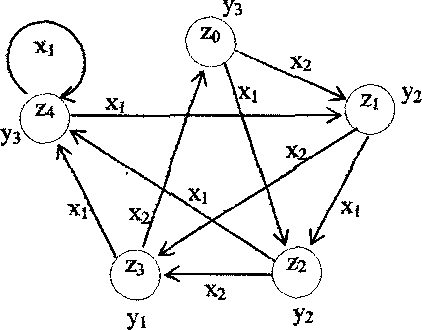
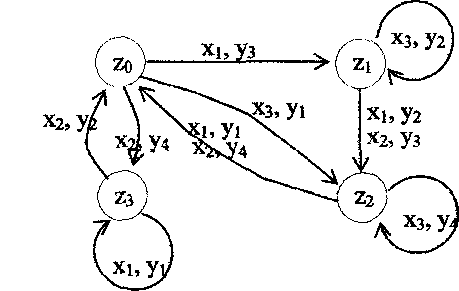
Рисунок 1.2 – Граф автомата а) Милі; б) Мура.