3. Расчет зубчатых колес редуктора

Выбор твердости, термическое обработки и материала

зубчатых колес

Так как в задании нет особых требований к габаритам передачи, то в приводах общего назначения для изготовления зубчатых колес редуктора выбираем материалы со средними механическими характеристиками с твердостью НВ350. При таких условиях на практике применяется один из вариантов (см. стр. 18) термической обработки (т.о.). Принимаем т.о. колеса – улучшение, твердость НВ 235262; т.о. шестерни – улучшение, твердость НВ 269302. Материал сталей одинаков для колеса и шестерни:

для шестерни — сталь 45, термообработка — улучшение, твердость 250 НВ; для колеса — сталь 45, термообработка — улучшение, но твердость на 50 единиц ниже (косозубая передача), т.е. 200 НВ.

Допускаемые контактные напряжения

[σ_Н] = σ_{Н lim b}  К_HL  Z_R  Z_v / [S_H],

где σ_{Н lim b} – предел контактной выносливости при базовом числе циклов (табл. 1.10) для углеродистых сталей с твердостью поверхностей зубьев менее 350 НВ и термической обработкой – улучшение: [σ_{Н lim b}] = 2  НВ + 70; [S_H] – коэффициент безопасности, [S_H] = 1,1, так как материал с однородной структурой; Z_R – коэффициент, учитывающий шероховатость сопряженных поверхностей зубьев, Z_R = 0,95 (R_a = 2,51,25); Z_v – коэффициент, учитывающий окружную скорость передачи, Z_v = 1 (для v  5 м/с); К_HL – коэффициент долговечности, определяется в зависимости от N_H0 – базовое число циклов напряжений, соответствующее пределу выносливости

(N_H0 = 30  Н^2,4 НВ  12010⁶) и N_HЕ – эквивалентное число циклов переменных напряжений.

При постоянной нагрузке и зацеплении с одним колесом N_HЕ = 60t_чn, где t_ч – полное число часов работы передачи за расчетный срок службы; n – частота вращения вала зубчатого колеса.

Тогда

σ_{Н lim b1} = 2  250 + 70 = 570 МПа; σ_{Н lim b2} = 2  200 + 70 = 470 МПа;

N_H01 = 30  250^2,4 = 1710⁶; N_H02 = 30  200^2,4 = 1010⁶;

N_HЕ1 = 60  n₂  t_ч = 60  1000  36  10³ = 216010⁶;

N_HЕ2 = 60  n₃  t_ч = 60  200  36  10³ = 43210⁶.

Отношения

N_HЕ1 / N_H01 = 216010⁶ / 1710⁶ = 127;

N_HЕ2 / N_H02 = 43210⁶ / 1010⁶ = 43,3.

При N_HЕ / N_H0 > 1 коэффициент долговечности равен К_НL = 1.

Для косозубых колес расчетное допускаемое контактное напряжение

[σ_Н] = 0,45  ( [σ_Н1] + [σ_Н2] );

для шестерни

[σ_Н1] = 570  0,95  1  1 / 1,1=492,3 МПа;

для колеса

[σ_Н2] = 470  0,95  1  1 / 1,1 = 406 МПа.

Расчетное допускаемое контактное напряжение

[σ_Н] = 0,45  (492,3 + 406) = 405 МПа.

Требуемое условие [σ_Н]=405 МПа 1,23 [σ_Н2]=1,23406=500 МПа выполнено.

Проектировочный расчет зубчатой передачи

Для редукторов общего назначения с внешним зацеплением определяем межосевое расстояние из условия контактной выносливости активных поверхностей зубьев

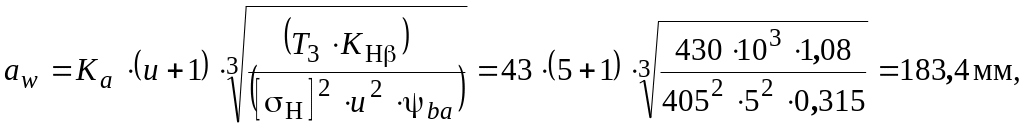
где для косозубых колес К_а = 43; u = u₂ – передаточное число редуктора; Т₃ – крутящий момент на валу колеса, Нмм; ψ_ba – коэффициент ширины венца по межосевому расстоянию, для передачи косозубой принимаем ψ_ba=b/а_w=0,315; К_Н – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца, определяется через вспомогательный коэффициент ψ_bd = ψ_ba (u+1) / 2 = 0,315(5+1)/2 = 0,945, по графику (рис. 3.2) К_Н= 1,08.

Ближайшее значение межосевого расстояния по ГОСТ 2185–66 а_w = 180 мм.

Нормальный модуль зацепления

m_n = (0,01 ÷ 0,02)  а_w = (0,01 ÷ 0,02 )  180 = 1,8 ÷ 3,6 мм,

принимаем по ГОСТ 9563-60 m_n= 2 мм.

Предварительно принимаем угол наклона зубьев β = 10 .

Определяем число зубьев шестерни и колеса

Принимаем z₁ = 29; z₂ = z₁  u₂ = 29  5 = 145.

Уточненное значение угла наклона зубьев :

,  = 1450'.

Основные размеры шестерни и колеса (рис. 3.3):

диаметры делительные d₁ = (m_n / cos β)  z₁ = ( 2 / 0,9666 )  29 = 60,00 мм;

d₂ = (m_n / cos β)  z₂ = ( 2 / 0,9666 )  145 = 300 мм;

проверка а_w = (d₁ + d₂) / 2 = ( 60 + 300 ) / 2 = 180 мм;

диаметры выступов зубьев d_а1 = d₁ + 2m_n = 60 + 22 = 64 мм;

d_a2 = d₂+2m_n = 300 + 22 = 304 мм;

диаметры впадин d_f1 = d₁ – 2,5m_n = 60 – 2,52 = 55 мм;

d_f2 = d₂ – 2,5m_n = 300 – 2,52 = 295 мм;

ширина колеса b₂ = ψ_bаа_w = 0,315180 = 56,7 мм; принимаем b₂ = 60 мм;

ширина шестерни b₁ = b₂ + 5 мм = 60 + 5 = 65 мм.

Коэффициент ширины шестерни по диаметру Ψ_bd=b₁/d₁ = 65/60 = 1,08.

Окружная скорость колес и степень точности передачи:

v = (ω₁d₁)/2 = (104,66  60  10 ^–3) / 2 = 3,14 м/с.

При такой скорости для косозубых колес принимают 8-ю степень точности по ГОСТ 1643 – 81.

Силы, действующие в зацеплении:

окружная F_t =(2  T₂ ) / d₁ = (2  T₃ ) / d₂ = (2  430  10 ³ ) / 300 = 2867 H;

радиальная F_r = F_t  ( tg α / cos β) = 2867  ( tg 20 / cos 0,966 ) = 1080 H;

осевая F_a = F_t  tg β = 2867  tg 1450' = 2867  0,2648 = 759 H.

Проверочные расчеты

Проверка контактных напряжений

Действующее в передаче контактное напряжение

где Z_H – коэффициент, учитывающий форму сопряженных поверхностей зубьев, Z_H = = = 2,378;  – основной угол наклона зуба,  = 14,833;  – угол зацепления,  = 20.

Коэффициент Z_М учитывает механические свойства материалов сопряженных колес. Для зубчатой передачи со стальными зубчатыми колесами Z_М = 190.

Коэффициент Z_ учитывает суммарную длину контактных линий. При _ < 0,9 Z_ = ; при _ > 0,9 Z_ = .

Коэффициент торцевого перекрытия

_ = [1,88 – 3,2 (1/Z₁ + 1/Z₂)]сos =

= [1,88 – 3,2 (1/29 + 1/145)]0,9666 = 1,689.

Коэффициент осевого перекрытия

_ = b sin / m = 60  0,256 / 3,14  2 = 2,446.

Тогда

Z_ = = 0,77.

Окружное усилие F_t = 2867 Н.

Значение коэффициента К_Нβ = 1,08 (ранее найдено по графику рис. 3.2).

Коэффициент, учитывающий распределение нагрузки между зубьями, К_Нα = 1,08 (табл. 3.16).

Коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении

К_Нv = 1 + w_Нv  b / F_t  К_Нα  К_Нβ,

где w_Нv – удельная окружная динамическая сила, Н/мм.

w_Нv = _Н  g₀  v  .

Коэффициенты _Н и g₀ выбираем по табл. 10.4 и 10.5 [4]. _Н = 0,02, g₀ = 5,6, окружная скорость v = 3,14 м/с. Тогда

w_Нv = 0,02  5,6  3,14  = 2,11 Н/мм;

К_Нv = 1 + 2,11  60 / 2866  1,08  1,08 = 1,023.

Контактное напряжение

.

 = {([_H] – _H)/ [_H]}100% = {(405 – 372)/405}100% = 8,1 % .

Допускаемое максимальное контактное напряжение

[_H]_max = 2,8  _т = 2,8  440 = 1232 МПа,

где _т = 440 МПа (табл. 3.10) – предел текучести.

Так как кратковременная нагрузка передачи больше номинальной в 1,6 раза, то

_Hmax = _H  = 372  1,6 = 595,2 МПа

_Hmax < [_H]_max = 1232 МПа.

Условие прочности выполняется.

Проверка зубьев на выносливость по напряжениям изгиба

Условие выносливости по напряжениям изгиба:

σ_F = ( F_t  K_F  Y_F  Y_β  K_Fα ) / ( b  m_n )  [σ_F] ,

здесь коэффициент нагрузки К_F = K_Fβ  K_Fv, где К_Fβ – коэффициент концентрации нагрузки, по табл. 3.18 К_Fβ = 1,33; K_Fv – коэффициент динамичности, по табл. 3.19: K_Fv = 1,3.

Таким образом, К_F = 1,33  1,3 = 1,73.

Коэффициент Y_F, учитывающий форму зуба и зависящий от эквивалентного числа зубьев z_v :

для шестерни z_v1 = z₁ / cos β = 29 / 0,966 = 32;

для колеса z_v2 = z₂ / cos β = 145 / 0,966 = 160;

Y_F1 = 3,78 и Y_F2 = 3,6.

Допускаемое напряжение на выносливость зубьев при изгибе

[σ_F] = σ_{F lim b} K_FL  K_FC / [S_F].

По табл. 3.10 для стали 45 улучшенной при твердости Н  350 НВ σ_{F lim b} = 1,8 НВ.

Для шестерни σ_{F lim b} = 1,8  250 = 450 МПа.

Для колеса σ_{F lim b} = 1,8  200 = 360 МПа.

Коэффициент безопасности

[S_F] = [S_F]  [S_F],

где [S_F] – коэффициент, учитывающий нестабильность свойств материала зубчатых колес, для стали улучшенной [S_F]= 1,75; [S_F] – коэффициент, учитывающий способ получения заготовок зубчатых колес, для поковок [S_F] = 1, тогда: [S_F] = 1,75  1 = 1,75.

Эквивалентное число циклов напряжений N_F0 = 410⁶, базовое число циклов напряжений

N_FЕ1 = 60  n₂  t_ч = 60  1000  36  10³ = 216010⁶;

N_FЕ2 = 60  n₃  t_ч = 60  200  36  10³ = 43210⁶.

Так как N_FЕ > N_F0, то коэффициент долговечности К_НL = 1, Коэффициент К_FC – одностороннее действие нагрузки.

Допускаемые напряжения: для шестерни [σ_F1] = 45011/1,75 = 257 МПа; для колеса [σ_F2] = 360 / 1,75 = 206 МПа.

Находим отношение [σ_F]/Y_F : для шестерни 25711/3,78 = 68 МПа; для колеса 20611/3,6 = 57,5 МПа.

Расчет ведем для зубчатого колеса, у которого найденное отношение меньше, т.е. для колеса.

Определяем коэффициенты Y_β и К_Fα:

Y_β = 1 – (β/140) = 1 – (14,83/140) = 0,894,

где  = 14,83 – угол наклона делительной линии зуба; К_Fα – коэффициент, учитывающий неравномерность распределения нагрузки между зубьями при упрощенных расчетах, К_Fα = 0,92.

Поверка прочности зуба колеса :

σ_F2 = ( F_t  K_F  Y_F2  Y_β  K_Fα ) / ( b₂  m_n )  [σ_F] ;

σ_F2 = (2867  1,73  3,6  0,894  0,92 )/( 60  2 ) = 122 < [σ_F2] = 206 МПа.

Максимальное допускаемое напряжение

[_F]_max = 0,6  _в = 0,6  690 = 414 МПа.

Так как кратковременная нагрузка передачи больше номинальной в 1,6 раза, то

_Fmax = 1,6  _F = 1,6  206 = 329,6 МПа

_Fmax < [_F]_max = 414 МПа.

Условие прочности выполнено.