8

Погрешности цифровых средств обработки

Введение

В каналах сбора и обработки измерительной информации современных информационно-измерительных систем определяются различные характеристики объекта измерения. В зависимости от вида решаемой задачи и природы объекта измерения выходными данными систем могут быть:

• параметры вероятностной модели, получаемые в процессе статистической обработки результатов многократных измерений;

• результаты аппроксимации статических характеристик в виде степенных полиномов или других функций;

• параметры эквивалентных схем или структурно-функциональных моделей;

• временные модели, характеризующие динамику изменения физических переменных и использующиеся для фильтрации или прогнозирования;

• результаты совокупных или косвенных измерений.

В процессе получения результата значительная часть операций, за исключением первичного преобразования, реализуется в числовой форме. Поступающие на вход процессора операнды содержат числовые эквиваленты истинного значения физической величины или константы и абсолютной погрешности. Обе составляющие подвергаются функциональному преобразованию, поэтому на выходе появляется так называемая наследственная погрешность как результат трансформации погрешности исходных данных.

Ограниченность размера разрядной сетки приводит к возникновению погрешности усечения машинного слова, которая по определению является инструментальной погрешностью. Погрешность усечения есть результат сокращения длины информационного слова при выполнении операций умножения, деления, суммирования с масштабированием. Погрешность усечения зависит от способа представления чисел и масштаба машинной переменной.

1. Инструментальные погрешности

Инструментальные погрешности являются первичными, так как возникают непосредственно в вычислительной среде. В качестве характеристик инструментальных погрешностей обычно используют математическое ожидание и дисперсию. При оценке характеристик первичных ошибок, представленных в числовой форме, предполагается статистическая природа переменных. Считается, что переменные случайны и заданы вероятностями появления единицы в каждом разряде мантиссы числа и вероятностями появления единицы в произведении двух любых разрядов.

1.1. Погрешность усечения

Простое усечение заключается в отбрасывании m разрядов машинного операнда и имеет место при выполнении операций умножения, деления и правого сдвига. Если в случайном машинном операнде x_n+m=0, b₁ b₂ … b_n b_n+1 … b_n+m отбрасываются m младших разрядов, получается новый операнд x_n=0, b₁ b₂ … b_n, отличающийся от исходного на величину случайной погрешности

.

Математическое ожидание погрешности определяется по формуле

. (1)

В каждом разряде b_i может принимать значения 0 или 1. Поэтому математическое ожидание M[b_i] равно вероятности появления единицы в соответствующем разряде P₁(b_i), которая при равновероятном законе распределения равна 0,5. Для любого другого закона распределения

. (2)

Для равномерного закона распределения b_i математическое ожидание погрешности отбрасывания равно

. (3)

Дисперсия погрешности (2) вычисляется по формуле

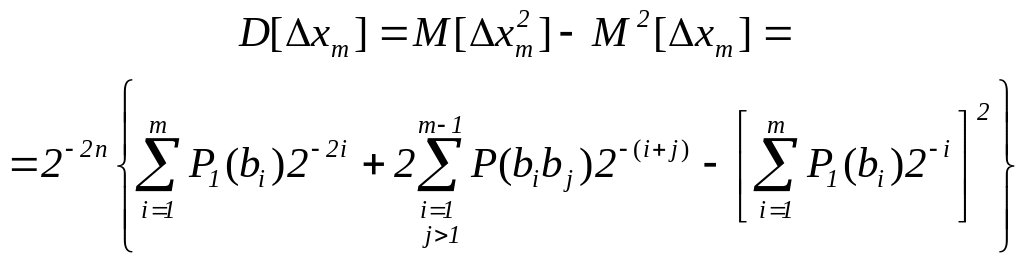, (4)

где P₁(b_ib_j) – вероятность появления единицы одновременно в двух разрядах мантиссы числа x_m.

Учитывая, что для равномерного закона распределения P₁(b_i)=0,5, P₁(b_ib_j)=0,25, значение дисперсии (4) равно

. (5)

Приближенные предельные значения характеристик случайной погрешности усечения (3), (5) находятся из предположения, что m>>1.