10. Практический пример реализации математики в архитектуре

Человек должен принимать решения относительно того, что численное совпадение действительно совпадение. Если рассмотреть одно из таких совпадений, связанное с золотым номером. Золотое число (1 + √ 5) / 2 = 1,618033989 и угол на основе этого будет иметь размер угловых секунд (1,618033989) = 51 ° 50 '. Стороны Великой Пирамиды как раз расположены под углом и равны = 51 ° 52 '.

Одним из современных мировых шедевров архитектуры, показывающий тесную связь математики и архитектуры является проект здания Огурца в Лондоне. Высота здания составляет 180 метров, что в три раза превышает высоту Ниагарского водопада. Существуют три основных особенности, которые выделяют его от большинства других небоскребов: это круглая, а не квадратная, она выпирает в середине и сужается к тонкому концу к вершине, и она основана на спиралевидные конструкции.

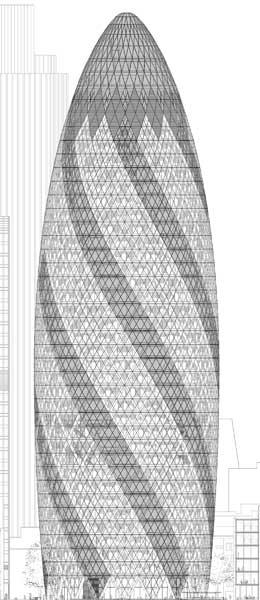
Основная проблема проектирования здания размером как Огурец - воздушные потоки, которые создают вокруг них вихри. Чтобы решить эту

проблему, архитекторами были использованы компьютерные модели, основанные на математической турбулентности, позволяющие моделировать аэродинамические свойства здания. Модель показала, что цилиндрическая форма лучше реагирует на потоки воздуха, чем квадратная и уменьшает вихри. Дело в том, что башня выпирает в середине, достигнув своего максимального диаметра на 16-м этаже, а также помогает свести к минимуму потоки ветра на ее более стройной части.

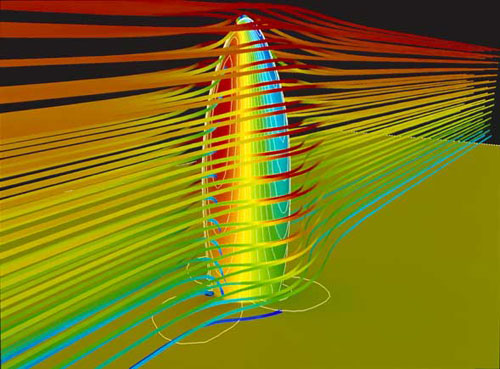
Модель потоков воздуха, Огурец. Image ©

Д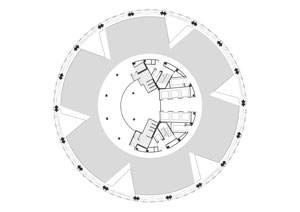 ругая проблема архитектурного моделирования этого здания - потеря солнечного света. Однако его выпуклые канонические части гарантируют, что вы никогда не увидите ее вершину снизу, а это в свою очередь, не заставит вас чувствовать себя совсем маленьким.

П

Пол Огурца план. Image © Foster + Partne

ри моделировании здания Огурца главной целью была его устойчивость, к которой добавлялась естественная вентиляция воздуха (чтобы сэкономить на кондиционирование воздуха) и приток естественного солнечного света (чтобы сэкономить на отоплении и освещении). Шесть треугольных клиньев были вырезаны из круговых планов каждого этажа, проникая глубоко в недра здания. Они служат световыми колодцами и создают естественную вентиляцию. Тем не менее, клинья не сидят прямо на верхней части друг друга. Аэродинамическое моделирование показало, что вентиляция будет максимальной, если план одного этажа поворачивается на несколько градусов ниже другого. В результате применения геометрии, здание потребляет на 50% меньше энергии, чем другие аналогичные объекты.

П

Внутри Огурца. Image © Foster + Partners

оверхности, которые можно описать математическими уравнениями, - такие, как конусы, торы, или сферы - часто образуют основу дизайна британских авторов. Это удобно, когда дело доходит до создания виртуальных моделей, посредством которых математически генерируется поверхность на компьютере.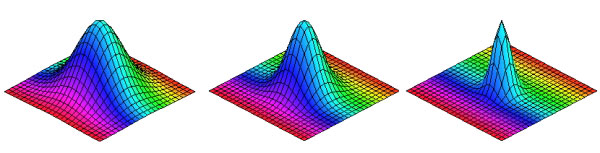

Эти поверхности являются графиками функции г = ^{е-(х 2 + у 2).} Здесь в 3-мерной системе координат формируется х, у, z. Число определяет форму поверхности. Первая поверхность = 1, вторая = 5, а третья z имеет = 7.