Задача 2.3.
О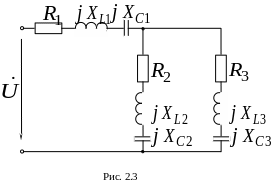
пределить
эквивалентное сопротивление цепи (рис.
2.3)
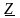в алгебраической и показательной форме
по данным табл. 2.3.
Таблица 2.3
Вариант |
Данные для расчета |
||||||||
Ом |
Ом |
Ом |
, Ом |
, Ом |
Ом |
, Ом |
, Ом |
Ом |
|
1 |
8 |
10 |
12 |
6 |
– |
– |
– |
12 |
– |
2 |
– |
14 |
– |
24 |
30 |
– |
10 |
– |
25 |
3 |
15 |
– |
5 |
– |
10 |
– |
18 |
– |
8 |
4 |
40 |
– |
20 |
– |
30 |
15 |
26 |
– |
– |
5 |
– |
28 |
– |
35 |
20 |
– |
– |
– |
42 |
6 |
– |
– |
15 |
– |
– |
20 |
24 |
36 |
– |
7 |
30 |
16 |
36 |
– |
– |
– |
– |
– |
26 |
8 |
– |
32 |
45 |
– |
24 |
– |
14 |
– |
– |
9 |
– |
48 |
– |
20 |
– |
80 |
– |
26 |
– |
10 |
22 |
– |
14 |
– |
17 |
– |
30 |
35 |
– |
11 |
18 |
– |
28 |
– |
– |
– |
– |
32 |
21 |
12 |
– |
12 |
25 |
36 |
26 |
– |
– |
– |
– |
13 |
– |
34 |
18 |
11 |
– |
2 Продолжение табл. 2.3 4 |
26 |
– |
– |
14 |
20 |
33 |
– |
– |
– |
40 |
– |
44 |
– |
15 |
12 |
24 |
– |
18 |
– |
34 |
– |
– |
20 |
16 |
– |
1 |
1 |
– |
– |
3 |
8 |
3 |
– |
17 |
1 |
2 |
4 |
– |
4 |
– |
– |
– |
2 |
18 |
10 |
20 |
20 |
– |
10 |
– |
– |
– |
10 |
19 |
– |
3 |
– |
7 |
– |
6 |
– |
4 |
8 |
20 |
6 |
10 |
– |
6 |
– |
– |
– |
– |
10 |
21 |
– |
1 |
1 |
3 |
7 |
– |
– |
– |
3 |
22 |
2 |
5 |
– |
– |
11 |
– |
2 |
– |
14 |
23 |
3 |
– |
8 |
– |
8 |
– |
– |
4 |
– |
24 |
10 |
– |
– |
15 |
– |
20 |
– |
10 |
– |
25 |
– |
– |
7 |
– |
– |
10 |
5 |
5 |
– |
26 |
– |
– |
5 |
2,5 |
– |
– |
– |
5 |
– |
27 |
6 |
– |
– |
– |
3 |
– |
– |
– |
6 |
28 |
– |
5 |
– |
– |
– |
5 |
4 |
– |
– |
29 |
3 |
– |
– |
4 |
6 |
– |
– |
– |
10 |
30 |
– |
2 |
– |
8 |
– |
– |
– |
– |
6 |
31 |
6 |
– |
4,5 |
– |
4 |
– |
8 |
– |
– |
32 |
– |
6,4 |
6,4 |
10 |
– |
– |
5 |
– |
– |
33 |
7 |
– |
4,4 |
– |
– |
– |
– |
3 |
– |
34 |
– |
– |
– |
– |
– |
– |
3,5 |
3 |
4 |
35 |
– |
– |
– |
6 |
6 |
8 |
– |
– |
– |
36 |
3 |
– |
– |
– |
5 |
– |
4 |
– |
10 |
37 |
4 |
4 |
– |
3 |
– |
– |
– |
5 |
5 |
38 |
– |
5 |
– |
8 |
– |
– |
6 |
– |
5 |
39 |
4 |
– |
– |
4,5 |
3 |
– |
– |
– |
7 |
40 |
2 |
– |
– |
– |
6,5 |
– |
– |
– |
3,5 |
41 |
– |
– |
6 |
3 |
– |
– |
– |
5 |
– |
42 |
7 |
– |
– |
– |
2 |
– |
– |
– |
6 |
43 |
– |
6 |
– |
– |
– |
7 |
3 |
– |
– |
44 |
3 |
– |
10 |
2 |
5 |
5 Продолжение табл. 2.3
|
– |
– |
– |
45 |
– |
2 |
– |
8 |
– |
– |
– |
– |
8 |
46 |
7 |
– |
– |
5 |
– |
5 |
– |
8 |
– |
47 |
– |
– |
6 |
7 |
11 |
– |
– |
8 |
– |
48 |
8 |
– |
– |
5 |
5 |
– |
– |
8 |
8 |
49 |
4 |
– |
– |
– |
5 |
– |
4 |
– |
6 |
50 |
– |
5 |
– |
9 |
– |
– |
5 |
– |
5 |
,
,
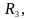
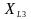