
- •Методические указания к выполнению контрольной работы
- •Методические указания к выполнению контрольной работы
- •Введение
- •1. Электрические цепи однофазного синусоидального тока
- •1.1. Переменные токи
- •1.2. Среднее и действующее значения синусоидально изменяющейся величины
- •1.3. Символический метод расчета цепей переменного синусоидального тока
- •1.4. Основные законы электротехники в символической форме Закон Ома
- •1) Активное сопротивление
- •2) Идеальная индуктивность
- •3) Идеальная емкость
- •Первый закон Кирхгофа
- •Второй закон Кирхгофа
- •1.5. Применение комплексных чисел к расчету цепей синусоидального тока
- •Переход от показательной формы комплексного числа к алгебраической
- •Переход от алгебраической формы комплексного числа к показательной
- •1.6. Активная, реактивная и полная мощность. Баланс мощностей
- •1.7. Цепи с взаимоиндукцией
- •2. Задание. Расчет линейных электрических цепей синусоидального тока Задача 2.1.
- •Задача 2.2.
- •Задача 2.3.
- •3. Типовой расчет задания «Расчет линейных электрических цепей синусоидального тока» Задача 3.1
- •Решение.
- •Задача 3.2
- •Решение.
- •Задача 3.2
- •Решение.
- •Список литературы
- •Содержание
- •1. Электрические цепи однофазного синусоидального тока
- •2. Задание. Расчет линейных электрических цепей синусоидального тока
- •3. Типовой расчет задания
1.2. Среднее и действующее значения синусоидально изменяющейся величины
Под средним значением синусоидально изменяющейся величины понимают среднее ее значение за полпериода.
Среднее значение синусоидального тока:
 ;
;
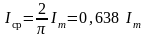 .
.
Аналогично получим среднее значение напряжения и ЭДС:
 ;
; 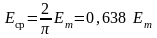 .
.
Среднее значение тока служит для сравнения постоянного и переменного тока по их электролитическому действию.
Тепловое действие тока пропорционально квадрату тока. Поэтому для суждения о величине периодического тока вводят понятие о среднем квадратичном значении тока за период, которое называют действующим значением переменного тока. Действующее значение синусоидального тока:
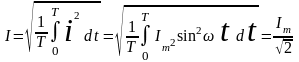 ;
;
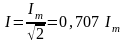 .
.
Аналогично получим действующие значения напряжения и ЭДС:
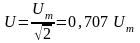 ;
; 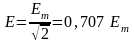 .
.
Действующее значение переменного тока численно равно такому постоянному току, который за один период выделяет в сопротивлении такое же количество тепла, как и ток переменный. Отсюда и одинаковое их обозначение. Действующие значения измеряют приборами электромагнитной, электродинамической и тепловой систем.
1.3. Символический метод расчета цепей переменного синусоидального тока
На рис 1.2 показано,
что синусоидальная функция
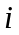 представляет собой проекцию на ось
мнимых величин
представляет собой проекцию на ось
мнимых величин
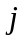 вектора длинною
при вращении его против часовой стрелки
с угловой скоростью
,
т.е.
вектора длинною
при вращении его против часовой стрелки
с угловой скоростью
,
т.е.
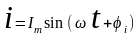 .
С целью упрощения расчетов синусоидального
тока удобно на момент расчета заменить
синусоиду изображающим вектором
,
называемым комплексной амплитудой.
.
С целью упрощения расчетов синусоидального
тока удобно на момент расчета заменить
синусоиду изображающим вектором
,
называемым комплексной амплитудой.
- комплексная амплитуда, определяет величину и положение вектора при .
Для любого момента времени
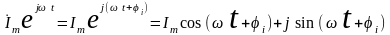 ;
;
 - действительная
часть вращающегося
- действительная
часть вращающегося
вектора;
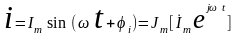 - мнимая часть
вращающегося вектора, представляет
собой мгновенное значение синусоидального
тока.
- мнимая часть
вращающегося вектора, представляет
собой мгновенное значение синусоидального
тока.
Можно вести расчет
не только с использованием комплексной
амплитуды
,
но и комплекса действующего значения
тока
 .
Необходимо четко усвоить связь между
следующими величинами:
.
Необходимо четко усвоить связь между
следующими величинами:
- мгновенное значение синусоидального тока;
- амплитуда;
 - действующее
значение синусоидального тока;
- действующее
значение синусоидального тока;
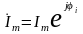 - комплексная
амплитуда синусоидального тока;
- комплексная
амплитуда синусоидального тока;
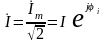 - комплекс
действующего значения синусоидального
- комплекс
действующего значения синусоидального
тока.
Метод расчета с использованием изображающих векторов или соответствующих им комплексных чисел называется символическим методом, т.к. действительные синусоидальные функции заменяют символами.
Напряжение и ЭДС можно представить аналогичными изображающими комплексами
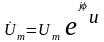 ;
; 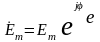 или векторами.
или векторами.
Совокупность
векторов, построенная с соблюдением
их взаимной ориентации по фазе, называется
векторной диаграммой. Векторную
диаграмму всегда изображают для момента
,
при этом начальную фазу соответствующего
вектора откладывают от оси действительных
чисел
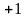 (рис.1.3). Углы, отложенные против часовой
стрелки - положительные, по часовой -
отрицательные. На рис. 1.3
(рис.1.3). Углы, отложенные против часовой
стрелки - положительные, по часовой -
отрицательные. На рис. 1.3
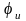 - положительный,
- отрицательный угол. Сдвиг по фазе
тока относительно напряжения
- положительный,
- отрицательный угол. Сдвиг по фазе
тока относительно напряжения
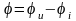 нужно показывать стрелкой от тока
к напряжению
нужно показывать стрелкой от тока
к напряжению
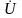 .
На рис. 1.3
.
На рис. 1.3
 - положительный. Основные законы
электротехники для цепей с
- положительный. Основные законы
электротехники для цепей с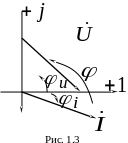 инусоидального
тока записывают для комплексных величин
или изображающих векторов, т. е. они
представляют геометрическую сумму в
отличие от цепей постоянного тока, где
суммирование алгебраическое. Символический
метод позволяет упростить расчеты, так
как вместо интегро-дифференциальных
уравнений для синусоид получаем
уравнения алгебраические для изображающих
векторов.
инусоидального
тока записывают для комплексных величин
или изображающих векторов, т. е. они
представляют геометрическую сумму в
отличие от цепей постоянного тока, где
суммирование алгебраическое. Символический
метод позволяет упростить расчеты, так
как вместо интегро-дифференциальных
уравнений для синусоид получаем
уравнения алгебраические для изображающих
векторов.
