3. Типовой расчет задания «Расчет линейных электрических цепей синусоидального тока» Задача 3.1

Э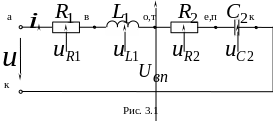 лектрическую цепь, схема которой изображена на рис. 3.1, рассчитать при частоте по данным табл. 3.1. Построить топографическую векторную диаграмму.

Таблица 3.1

Вариант	Данные для расчета						Определить
	Ом	Ом	мГН	мкФ	Uвп В	град
101	3	1	22,3	318	21,15	30	i	u	Uао	P	Q	S

На схеме показать только заданные элементы.

Решение.

1) Определим мгновенное значение тока

.

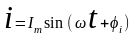- амплитуда тока, .

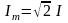- действующее значение тока,

Определим реактивные сопротивления цепи:

;

;

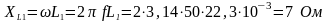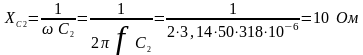Угловая частота .

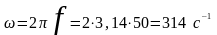Величина сопротивления участка цепи вп:

.

.

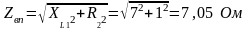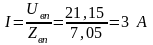Начальная фаза тока 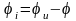, где

- начальная фаза напряжения,

- угол сдвига фазы тока по отношению к фазе напряжения.

Угол определяем из треугольника сопротивлений (рис. 3.2):

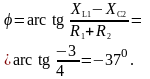
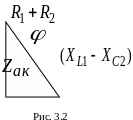
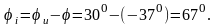
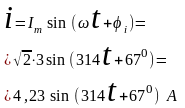
2) Мгновенное значение напряжения источника

.

.

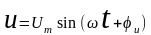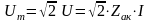Полное сопротивление цепи

.

.

.

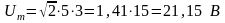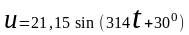3) Действующее значение напряжения на участке ао:

.

4) Активная мощность

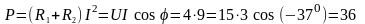Вт.

5) Реактивная мощность

.

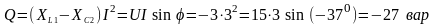6) Полная мощность

.

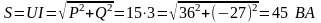7) Для построения топографической векторной диаграммы (рис. 3.3) необходимо сначала рассчитать комплексные напряжения на каждом элементе схемы, а затем начать построение диаграммы с общей величины – вектора тока , после чего построить последовательно друг за другом вектора напряжений, начиная с .

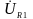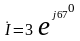
Вектор тока под углом 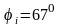к оси можно отложить в любом масштабе, масштаб напряжения . Все вектора связывают с осью , фазовый сдвиг указывают стрелкой от тока к напряжению.

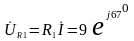- вектор совпадает по фазе с .

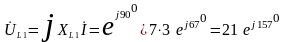- чтобы получить направление , вектор вращаем на (против часовой стрелки).

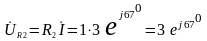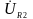- проводим параллельно току.

- чтобы получить направление 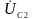необходимо вектор повернуть на (по часовой стрелке).

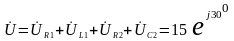- из расчета.

Убедимся из диаграммы, что суммарный вектор равен напряжению источника: , измеряем .

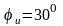З начит, расчеты выполнены верно.

Задача 3.2

Р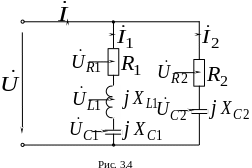 ассчитать электрическую цепь, схема которой изображена на рис. 3.4, по данным таблицы 3.2. Построить векторную диаграмму. Подсчитать баланс мощностей.

Таблица 3.2

Вариант	Данные для расчета						Определить
	Ом	Ом	, Ом	, Ом	, Ом	I1, A
101	4	8	6,64	3,32	6	4		I2	I	U

На схеме показать только заданные элементы.