4.10. Қанның пульсты ағысындағы микроконтинуалды моделі

Органикалық емес материалдардың жалпы серпімді микрополярлы теориясы гидродинамикады қолданылады. Оның негізін салушы ағайынды бауырлар Эжен және Франсуа Коссерлер болып табылады. Алайда, бұл теория Гюнтер, Трудсделл, Тупин, Гриоль, Миндлин, Кувшинский, Аэро, Пальмов, Эринген, Сухуби, Новацкий зерттеулерінің арқасында біршама интенсивтә өрлеуге жетті. Биологиялық сұйықтыққа Клайн мен Аллен [4] қолданды. Аз диаметрлі тамырларда немесе қылтамырда классикалық гидродинамика ретінде түсіндіруге болмайтын сипаттамалар тексеріледі. Сол себепті осы тамырда қанның микроциркуляциясы үшін микронтинуалды ортп теориясын қолдану қажет.

Дебнат микроротациондық әсер беретін қатты сфералық бөліктерді құрайтын сұйықтық үшін Эрингеннің микрополярлы теориясын қолданды. Қанды осындай әдіспен модельдей отырып, берілген радиуста қатты домалақ түтікте қан қозғалысының тұрақтылығын тексерді.

Модельдің негізгі сипатиамалары:

• қан - плазманы және ілінген қатты эритроциттерді қамтитын екі фазалы сұйықтық ретінде қарастырылады;

• қан - сығылмайтын сұйықтық болып табылады, сол себепті үзіліссіздік теңдеуі мына түрді қамтиды:

• div ̅v = 0 (4.81)

• ағын мына мәнге сәйкес осьсимметриялы болып тұжырымдалады:

• v_r = v₀ = 0, σ_r = σ_z = 0; (4.82)

• домалақ түтік жартылай шексіз (0 ≤ z ≤ ∞) болып саналады, ағыннан кейін түтікке мүмкіндік бар

186-193БЕТ

• қантамырлар тарамдануының басқа барлық әсерлерін есепке алмауға болады; түтіктің радиальды орын ауыстыруы орташа радиусты түтікпен салыстырғанда аз деп есептеледі;

• ̅f көлемді күштер және ̅k көлемді моменттер болмайды;

• жүйеде орнатылмаған ағын тәуелсіз z, t айнымалыларымен осьтік ағынның функциясы болып табылатын қысым градиентіне жалғанады.

Қанның тұрақсыз осьсимметриялық ағуынан дөңгелек түтікте v_z жылдамдық және σ₀ микроайналу жылдамдығы төмендегіше болады:

v_z ≡ v(r, z; t), σ_ө = σ(r, z; t).

Осы пайымдаулар салдарынан жеке туындыларды бейсызықты дифференциалды теңдеулер алынды:

ρ* +(µ*+γ*) ² v+ (r σ); (4.83)

ρ*j*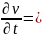 γ* + (4.83)

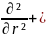
мұндағы ² ≡ ∆ = 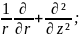ρ* - нәтижелі тығыздық; v - жылдамдық; ̅σ - микроайналудың векторы; р - белгісіз немесе берілген қысым; μ*, γ*, j*- қарастырылған сұйықтықтың әсерлі сипаттамасы.

σ =0 кезінде микроструктура мен макроскопиялық қозғалу арасында өзарабайланыс болмайды.

Қорытынды сұрақтар

1. Қантамыр радиусы 30% - ға кішірейеді. Қан ағынының көлемді жылдамдығы қысымның өзгеріссіз түсуінде қалай өзгереді?

2. Егер капиллярдың гидравликалық кедергісі 20% - ке өссе, диастоланың бас кезінде қысым түсуінің жылдамдығы неше рет өзгереді?

3. Қан, бұл - сұйықтық және төмендегілердің қайсысының тұтқырлық коэффициенті

1) ньютондық;

2) ньютондық емес;

3) біркелкі;

4) суспензия;

5) η = const;

6) η - ағын шартының фцһункциясы

Жауаптар:

а) 1, 3, 6;

б) 2, 4, 5;

в) 1, 3, 5;

г) 2, 4, 6.

4. Ірі қантамырда біруақытта төмендегі процесс болады:

а) қан бөлігінің орын ауыстыруы;

б) тамырлы толқынның таралуы;

в) дыбысты толқынның таралуы.

Бұл процестің сипаттамалық жылдамдығы қандай?

x) 1500м/с;

y) 10м/с;

z) 0,5м/с.

Жауаптар:

1) аz, бy, вz.

2) аz, бx, вy.

3) аx, бy, вz.

5. Қантамырдың бас жағынан 5см қашықтықта қан қысымын есептеу. Егер қантамырдың бас жағында қысым 10⁴ Па, қантамыр радиусы 1мм, тұтқырлық 0,005 Па·с, қан ағысының сызықты жылдамдығы 20 см/с болса.