
- •3.1. Бұлшықет ұлпасының феноменологиялық әдістері
- •3.2 Хилл моделі. Жеке жиырылу қуаты.
- •3.3. Құрылымдық амал негізіндегі бұлшық еттің функциялану әдісі
- •3.4 Бұлшықет қызметін модельдеуге құрылымдық–феноменологиялық тәсіл
- •3.5 Адамның тірек–қозғалғыштық жүйесінің құрылымдық–феноменологиялық моделі.
- •3.6. Бұлшықеттің жұмыс істеуінде температураның және вибрацияның рөлі
- •5.2. Қантамырдың локальды тарылуы кезіндегі қан ағысының ерекешеліктері. Резистивті модель
- •3.7. Биомеханикалық модельдерді спортта қолдану
- •4 Тарау Жүрек-қантамыр жүйесінің механикасы
- •4.1 Қанайналым жүйесінің функционалдық сызбасы.
- •4.2. Жүрек динамикасын модельдеу
- •4.11 Сурет- Жүректің ортаңғы бетінің жақындатылған формасы.
- •4.12 Сурет – Жүректің көлденең қимасының ортаңғы бетінің жақындатылған формасы.
- •Жүректің энергетикасы
- •4.3. Бұлшықеттің қанмен қамтамасыз етілу сұлбасы
- •Қанның және тамырлардың механикалық қасиеттері. Құрылымы бар орталардың тиімді модельдері (үлгілері) туралы түсінік
- •4.5 .Гемодинамикасының кейбір модульдері мен заңдары.
- •4.6. Икемді қантамырда қан ағысының кинетикасы Лүпілді толқын. Франк моделі.
- •4.7 Физико - механикалық құрылымының есебімен күретамырда қанның ағуы және қысымы
- •4.8. Қантамыр геометриясының ағынға әсері
- •Көктамырда қанның ағысы және қысымы
- •4.9. Қанның микроциркуляциясы
- •4.10. Қанның пульсты ағысындағы микроконтинуалды моделі
- •5 Бөлім. Капиллярдағы және локальды тарылған қантамырдағы гемодинамика
- •5.1. Капиллярда қанның фильтрленуі және реабсорбтылығы
- •5.2. Қантамырдың локальды тарылуы кезіндегі қан ағысының ерекешеліктері. Резистивті модель
- •5.2. Қантамырдың локальды тарылуы кезіндегі қан ағысының ерекешеліктері. Резистивті модель
- •3. Қан тұтқырлығының өзгеруі
4.7 Физико - механикалық құрылымының есебімен күретамырда қанның ағуы және қысымы
Ұзындығы және ені бойынша қантамырда ағын өзгеруінің есебімен қан ағысы процесінің моделдеуін, құрылымын және қанның физико - механикалық құрылымын қарастырамыз.
0,1 - 1,0 см диаметріндегі көлемді қантамырларда эритроциттің қатысты өлшемі аз (8∙10-4 см), сол себепті ортаның әсерлі моделін қолдануға болады.
Орташа есеппен күретамырларда қан өзін әсерлі тұтқырлық сұйықтығы секілді көрсетеді. Оның ағуы сығылмау div v͞ = 0 есебінен Навье - Стокс теңдеуімен сипатталып, төмендегі теңдеуді қамтиды:
ρ
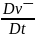 -
η*
-
η*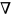 2
͞v
+ grad p = ͞F, (4.59)
2
͞v
+ grad p = ͞F, (4.59)
мұндағы ͞F - орта күшінің тығыздығы; ρ - тығыздық; η* - әсерлі тұтқырлық.
Ось симметриялық толқын таралуын зерттеу кезінде, қысым ("лүпілді толқын") күретамыр бойынша формулада жеделдету есепке алынбай, конвективті мүшемен теңестірілу - цилиндрлі координатада жазылады. Бұл сәйкес күретамырдың диаметрімен салыстырғанда тамырлы толқынның үлкен ұзындығымен айтылған.
Навье - Стокс теңдеуінің түрлендірілуі мына түрді қабылдайды:
 ,
,
(4.60)
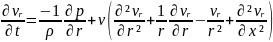 ,
,
ал жарылмаушылық теңдігі
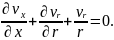 (4.61)
(4.61)
Егер х осі күретамыр бойымен бағытталған деп есептесек, (4.59), (4.60) теңдіктерінде v* = (η*/ρ) - жылдамдықтың бойлық және радиалды компоненттері, vx vr - кинематикалық тұтқырлықтың әсерлі коэффициенті.
Лүпілді толқын таралуының зерттемесін жүргізу кезінде (4.60), (4.61) формулаларға тамыр қабырғаларының қозғалысын сипаттайтын теңдеулерді қосу қажет. Бұл теңдеулер келіп түскен алғышартқа байланысты тамыр қабырғасы негізінің механикалық мінездемесін модельдейтін түрлі формаларға ие болады.
Уақыт мезетін есепке ала отырып, күретамырды жұқа қабырғалы цилиндрлік қабықша немесе қалың бүйірлі цилиндрлік түтікше ретінде қарастыруға болады. Қабырға материалы механика - математикалық модельдің 1 - бөлімінде атап өтілген сәйкестікпен қабылданады. Теңдеулерде қозғалысты in vitro қылтамырының физиологиялық күйіне сәйкес келетін алдын ала жетілудің қолда бары деп қабылдауға болады.
Мысал негізінде Кокспен ұсынылған күретамыр қабырғасы қозғалысының теңдеуін келтіреміз. Қантамыр - изотропты, сызықты, тұтқырсерпімді материалдан алынған қалыңбүйірлі цилиндрлі түтік ретінде қарастырылды. Бастапқы күш есепке алынбайды. Бұл теңдеулер мына түрді қамтиды:
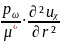 =
=
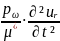 =
= (4.62)
(4.62)
 =0,
=0,
мұндағы ux, ur - қабырғаның орын ауыстыру компоненті;
μ* - қабырға қаттылығының әсерлі динамикалық модулі;
Ω - материалдың сығылмау себебінен келтірілетін ақырғы қысымы;
ρω - қабырғаның қаттылығы.
(4.62) теңдеуде соңғы теңестіру қабырға материалының сығылмау шартын көрсетеді.
a және b арқылы ішкі және сыртқы радиустарды белгілейміз. Онда тапсырманың шекті шарттары.
r = a кезіндегі
vr=0,

r = b кезіндегі
vr=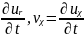 ;
;
r = a кезіндегі
µ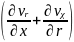 =µ*
=µ*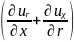 ,
(4.63)
,
(4.63)
-p+2µ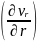 =-Ω+2µ*
=-Ω+2µ*
r = b кезіндегі
µ* =0,
-Ω+2µ*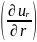 =0.
=0.
Қозғалыс теңдеуінің шешімі шекті шарт есебімен бірге Фанг бойынша берілген.[4] Ол қантамырларда толқынның таралу зерттемесінің кейбір ерекшеліктеріне мән береді. Теориялық және эксперименттік нәтижелерді салыстыру кезінде жұқа қабырғалы түтіктерге қарағанда, қалың бүйірлі түтіктер үшін теориялық нәтижелер анығырақ екені анықталды. Егер түтік қалыңдығының радиусқа қатынасы 1:20 аз болса, онда теория мен эксперимент арасындағы сәйкестік бұзылады. Мұның себебі, жұқа қабырғалы түтікте геометрияның жетілмегендігі, материалдың әртектілігі және бастапқы күштің ескерілмеуінің өте анық байқалғандығымен болжамданады.
Рейнольдстың жоғары санында тұтқырлықтың себебінен ақырын толқынға қарағанда, жылдам толқын үшін баяулану әлдеқайда жоғарырақ. Рейнольдстың төменгі санында ақырын (медленные) толқындар тезірек басылып қалады. Сұйықтықтың тұтқырлығы - қабырға материалының тұтқырсерпімділігіне (толқынның екі түрі үшін) қарағанда, осы әсерге азырақ ықпал етеді деп тұспалданады.
Атабек, қоршаған жасушаның әсерінен және бастапқы күш есебімен мембрана теориясымен жалғанатын қозғалысты жұқа ортотропты цилиндрлі қабықша ретінде қарай келе, қантамырдың басқа түрін ұсынды.
Келтірілген әдіске сәйкес, қабықша қозғалысының теңдеуі төмендегі түрде қабылданады:
M0 r=a
+
r=a
+

(4.64)
M0 r=a
+
r=a
+
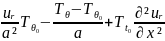 .
.
(4.64) - теңдеуінде ux, ur - лүпілді толқынмен шақырылған қабықшаның орталық бетінің бойлық және радиалды ауыстыруы; μ = vρ; a - алдын ала шиеленіскен қабықшаның орталық бетінің радиусы; М0 = ρ0 h + Ma (ρ0 - қабықша материалының тығыздығы); h - қабықшаның қалыңдығы; бұл жерде бастапқы бойлық және сақиналық күш, сонымен бірге жасуша қантамырын қоршаған әсер де есепке алынған; К1, С1, Ма - бойлық бағытқа сәйкес келетін жасуша беті ауданы бірлігіне қосымша масса, тұтқырлық коэффициенті және жасуша коэффициенті; Тx, Тө - қабықшаның орталық бетіндегі толықтай бойлық және қоршалған күші; Тxₒ , Төₒ - олардың бастапқы сәйкес мәндері. [20]
Лүпілді толқын үлкен бастапқы деформацияға жүктелетін шағын деформацияны шақырады деп есептейміз. (4.64) формуласын ux, ur қосымша ауыстырулармен Тө - Төₒ, Тx - Тxₒ - қосымша күштерді байланыстыратын физикалық күй теңдеулерімен толықтыру қажет. Бұл жұмыста [29] қантамырдың физикалық күйінің серпімді моделі қолданылды. Жөнделген модельды қарастырамыз [30].
Бұл модельге сәйкес, қантамыр қабырғасының моделі арақатынаспен анықталатын тұтқырсерпімді және ортотропты болып қабылданады.
TӨ
– TӨ₀=B₁₁ ,
Tx
–
,
Tx
–
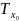 =B₂₁
=B₂₁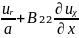 ,
(4.65)
,
(4.65)
мұндағы
Вij
z=DDij
J*ij(z);
J*ij(z)=z- i, j=1,2;
i, j=1,2;
D₁₁= D₁₂=
D₁₂=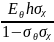 ;
D21=
;
D21= ;
D22=
;
D22= .
.
Бұл жерде Еө - σө - қоршалған бағытта Пуассон коэффициенті және Юнгтың шұғыл модулі; Ех, σх - бойлық бағыттағы ұзындықтар; Кij(ө) - тұтқыр серпімді материал кернеуі релаксациясының жылдамдық ядросы.
Кij(ө) = 0 екенін ескере келе, қантамырдың серпімді моделіне ауысамыз [4].
J*ij(z) интегралды операторын түрлендіреміз.
J*ij(z)=z-
-

екені белгілі
Теореманы екінші интегралға орташа күйде қабылдай отырып, ядро басылған жады қасиетін қанағаттандырады деп тұспалдай келе, J*ij(z)-T интегралды операторын келесі түрде жазуға болады:
J*ij(z) = z - ∫t-∞ Кij(t - τ)z (τ)dτ.
Қантамыр мен ағын сұйықтық арасындағы әрекеттестік шекті талаптармен есептеледі:
vr
(r, x, t)ǀr=a
=
 ,
vx
(r, z, t)ǀr=a
=
,
vx
(r, z, t)ǀr=a
=
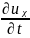 (4.66)
(4.66)
(4.60), (4.64), (4.65) теңдеулерінің жалпы шешімі келесі түрде көрсетіледі:
Бұл жерде ω - еріксіз тербелістің айнымалы жиілігі (нақты сан); с - толқын таралуының және оның басылуының фазалық жылдамдығымен байланысқан комплексті ұзындық; J0(x), J1(x) - нөлдік және бірінші қатарға сәйкес Бесселей функциясының алғашқы тегі; α0, β0 - α02 = i3a2ω /v = i3α2 cекілді өлшемсіз параметрлер; β0 = iaω / c = iβ; A1, A2 - тұрақты интегралдау (тағы екі тұрақтылар - A3, A4 - қолайсыздық есебінен бұл жерге жазылмаған ͂ur, ͂ux функцияларының теңдеуіне кіреді).
(4.67), (4.68) функцияларын және (4.65) - теңдеуде ͂ur, ͂ux үшін сәйкес шешімдер, сонымен қатар (4.66) ұшырасу шартынан Аі тұрақтысына қатысты алгебралық теңдеудің төрт жүйесін аламыз. Бұл жүйенің нетривиалды шешімінің бар болу шарты с шартты параметріне қатысты жиілік теңдеуін береді.
Егер
Моэнс - Кортэвэгтің с0
=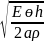 толқынды
жылдамдығын енгізетін болсақ және с0
/ с =X - iY мәнін
қабылдасақ, онда
толқынды
жылдамдығын енгізетін болсақ және с0
/ с =X - iY мәнін
қабылдасақ, онда
exp[iω(t-x/c)]
= exp[iω(t-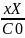 )]exp[-2π
)]exp[-2π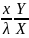 ],
(4.69)
],
(4.69)
мұндағы - тербеліс толқынының ұзындығы; с0 / Х - толқын таралуының жылдамдығы; к = exp(-2 πY / X) - қоршаған жасуша мен қантамыр материалының тұтқырсерпімді қасиетімен алынған толқын амплитудасының басылу есебінен оның ұзындығының бірлікке азаюын сипаттайтын жіберілу коэффициенті.
Жұмыста орындалған есептеулер [30] қантамыр қабырғасының серпімділік қасиетінің есептемесі с1 / с0, с2 / с0 топтық жылдамдықтың, сонымен бірге қанда баяу және тез толқын үшін к1, к2 жіберу коэффициенттердің төмендеуіне алып келеді.
Уомерсли vx, vr жылдамдықтарының с толқын жылдамдығынан әлдеқайда аз және толқын ұзындығының R радиустан анағұрлым үлкен екендігінен (4.62) - теңдеуді жеңілдетті.
Осы алғышарттың алдында (4.62) теңдеуін бір теңдеуге қысқартты:
∂v
/ dt = f -
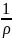 (∂p
/ ∂x), (4.70)
(∂p
/ ∂x), (4.70)
мұндағы v - локальды қимаға орташа жылдамдықтың қатынасы; f - экспериментті түрде немесе қалың түтік шешімінен анықталатын үйкеліс күші.
Біркелкі ағыс кезінде v - орташа жылдамдықтың қолданылу жағдайында үзіліссіздік шартын А(х), v және t ағыстарының арасындағы байланыспен алмастыру қажет.
in vitro тексерісінің негізінде қантамыр қабырғасы қоршаған жасуша кедергісінің салдарынан өте аз бойлық ауыстыруды қамтиды деп қабылданады. Сол себепті (4.62) - теңдеуде ux - ауыстыруы есепке алынбайды.
Теңестіру теңдеуі енгізіледі
∂A / ∂t + ∂(Аv) / ∂x = 0. (4.71)
Үйкелісті ескермей және қиманы тұрақты деп есептеп, толқын таралуының теңдеуі тегіс толқынның теңдеуіне келтіріледі:
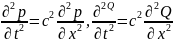 (4.72)
(4.72)
мұндағы
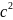 = А / [ρ(∂p
/ ∂A)]; Q
- уақыт бірлігінде өткен қан көлемі.
= А / [ρ(∂p
/ ∂A)]; Q
- уақыт бірлігінде өткен қан көлемі.
Бұл теңестіру жүйесінің шешімі төмендегі түрді қамтиды және +х, -х бағыттарында тарайтын қарапайым толқынның суммасы болып табылады.
p(x,
t) = f1(t
-
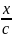 )
+ f2(t+
);
(4.73)
)
+ f2(t+
);
(4.73)
Q(x,
t) =
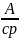 [f1(t
-
)
- f2(t
+
[f1(t
-
)
- f2(t
+
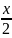 )]
(4.74)
)]
(4.74)
p(x, t) және Q(x, t)шекті мәндерінің негізінде қантамыр аймағының қарастырылып жатқан соңғы бөлігінде беріледі, ал бастапқы бөлік негізінде мәні t = 0.
Тамырлы толқынның таралу параметрлерінің зерттемесіне үлкен қызығушылық in vivo есебінде өлшеуге болатындығымен шарттасқан.
Бұл құбылыстың механика - математикалық модельдеуі - диагностикалық мақсатта (патологиялық өзгерістер эксперименттік және аналитикалық есептемеде толқын жылдамдығының негізінде қантамыр қабырғасында бағаланады) алынған шешімдерді қолдануға мүмкіндік береді. Ол үшін артериялық қысымның өзгеру негізінде тамырлы жасушаның бейсызықты механикалық қасиетін есепке алатын теориялық модель қабылданған.
Қабырға қозғалысының теңдеуі аз деформацияны шекті деформацияға салу теориясының көмегіен алынған. Материал сығылмайтын, изотропты және серпімді болып қабылданған, ал қантамыр цилиндрлі қабықша түрінде қарастырылған. Кейінірек жұмыр бұлшықеттің белсенді қасиеті есебімен ортотропты бейсызықты материал үшін қорытынды берілді. Қантамырдың нақты типі үшін сандық есебі келтірілген. Бұл артериалды қысым мен тамырлы толқын жылдамдығының мәліметтері бойынша артериалды қантамырлардың механикалық құрылымын анықтау әдісін ұсынуға рұқсат етті.
Қантамырда Коротков дыбысының генерирленуі де қарастырылуда. Бұл дыбыстар қан қысымын анықтау үшін қолданылады. Олар резеңке манжетке кигізілгенде систоликалық қысымға қарағанда жоғары қысымның кезінде пайда болады. Екінші этапта бронхиалды қантамырдағы қасиеттер естіледі. Бұл дыбыстардың түсіндірілуі Бертан бойынша берілген. Олардың пайда болуы қан ағынының турбуленттілігімен пайымдалады.
