Лекция 4 четырехполюсники
3.19 Четырехполюсники и их уравнения
Электротехнические устройства, имеющие два входных и два выходных зажима, называют четырехполюсниками. Четырехполюсники служат для передачи электрической энергии и электрических сигналов. Сюда относятся линии электропередачи, трансформаторы, усилители, фильтры и другие устройства, имеющие две пары зажимов. Одна пара зажимов из четырех (четырех полюсов) называется входными зажимами (1 и 1'), другая пара — выходными (2 и 2') (рисунок 3.37).
Рисунок 3.37 — Условное изображение четырехполюсника
Внутренняя цепь четырехполюсника, изображенная на рисунке 3.37 прямоугольником, может быть сколь угодно сложной. Если четырехполюсник имеет внутри себя источник энергии, то внутри прямоугольника ставят букву «А» (активный). Если буква «А» отсутствует, то четырехполюсник пассивный. При указанных на рисунке 3.37 положительных направлениях токов и напряжений в любом пассивном линейном четырехполюснике напряжение и ток на входе и связаны с напряжением и током на выходе и двумя уравнениями:
;
(3.82)
.
(3.83)
A, B, C, D — коэффициенты четырехполюсника, определяемые сопротивлениями его внутренней цепи. Коэффициенты связаны между собой уравнением:
.
(3.84)
Докажем справедливость
уравнений (3.82), (3.83), (3.84). Пусть к выходным
зажимам подключен приемник с сопротивлением
Z2,
а к входным — источник ЭДС
,
при этом
,
а
(рисунок 3.38, а).
а)
б)
Рисунок 3.38 — Электрическая цепь с четырехполюсником
Приемник с сопротивлением Z2 заменим, согласно принципу компенсации, источником ЭДС , численно равным напряжению и направленным навстречу току (рисунок 3.38, б). Определим токи и , используя принцип наложения:
;
.
Знак «минус» перед составляющими токов, вызываемых ЭДС , объясняется тем, что эти составляющие направлены противоположно составляющим, вызываемым ЭДС , и противоположны произвольно выбранным положительным направлениям токов и .
— входная
проводимость со стороны зажимов 1 и 1',
она равна отношению тока
к ЭДС
при
.
Аналогично
— входная проводимость со стороны
зажимов 2 и 2',
равная отношению тока
к ЭДС
при
.
— взаимная
проводимость. Она равна отношению тока
к ЭДС
при
.
— взаимная
проводимость, равная отношению тока
к ЭДС
при
.
Взаимные проводимости
и
равны друг другу:
,
— что следует из принципа взаимности.
Так как
;
;
,
то
;
(3.85)
.
(3.86)
Из (3.86) имеем
.
(3.87)
Подставив (3.87) в (3.85), получим
.
(3.88)
Обозначим
,
,
,
.
(3.89)
С учетом (3.89) уравнения (3.87) и (3.88) приобретают вид:
; (3.90)
. (3.91)
Докажем справедливость уравнения (3.84), подставив в него значения коэффициентов (3.89):
.
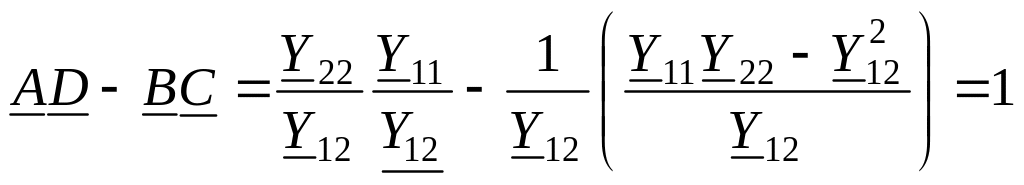Если в схеме четырехполюсника (рисунок 3.38, а) поменять местами источник ЭДС и приемник , а также поменять местами токи и , изменив при этом их направления на противоположные (рисунок 3.39), то с учетом всех этих изменений уравнения (3.82) и (3.83) примут вид:
;
(3.92)
.
(3.93)
Рисунок 3.39 — Четырехполюсник с источником ЭДС, включенным со стороны выхода
Решая полученную систему уравнений (3.92) и (3.93) с учетом (3.84), получим
;
(3.94)
.
(3.95)
Таким образом, если поменять местами вход и выход четырехполюсника (при обратном питании), коэффициенты A и D в уравнениях четырехполюсника меняются местами. Четырехполюсник называется симметричным, если при перемене местами источника энергии и приемника токи источника энергии и приемника не изменяются. В симметричном четырехполюснике A = D.
Уравнения (3.82) и
(3.83) являются наиболее распространенной
формой записи уравнений четырехполюсника.
Они позволяют выразить входные величины
и
через выходные
и
.
Возможны еще пять вариантов сочетания
двух известных и двух неизвестных
величин из четырех. Соответственно,
имеется шесть форм записи уравнений
четырехполюсника, при этом уравнения
(3.82) и (3.83) записываются в виде A-формы
(коэффициенты четырехполюсника A;
B;
C;
D
заменены соответственно на коэффициенты
A11;
A12;
A21;
A22):
A-форма:
,
;
Y-форма:
,
;
Z-форма:
,
;
H-форма:
,
;
G-форма:
,
;
B-форма:
,
.
Для форм Y, Z, H, G направление тока противоположно изображенному на рисунке 3.38. Для B-формы токи и противоположны изображенным на рисунке 3.38.
Коэффициенты уравнений одной из форм могут быть выражены через коэффициенты любой другой формы уравнений [2].