3.11 Опытное определение взаимной индуктивности

Взаимную индуктивность M можно определить опытным путем двумя способами.

Первый способ основан на поочередном включении двух катушек последовательно согласно и встречно. В обоих случаях измеряют ток, напряжение и активную мощность (рисунок 3.24), после чего определяют активное, полное, индуктивное сопротивление.

При согласном включении:

, , .

Рисунок 3.24 — Схема экспериментальной установки для определения взаимной индуктивности при последовательном включении катушек

При встречном включении:

, , .

Так как X_C = ωL₁ + ωL₂ + 2ωM, а X_B = ωL₁ + ωL₂ – 2ωM, то X_C – X_B = 4ωM.

Таким образом, взаимная индуктивность

M = . (3.52)

Второй способ основан на явлении взаимоиндукции. Две катушки включают по схеме трансформатора (рисунок 3.25).

Рисунок 3.25 — Схема экспериментальной установки для определения взаимной индуктивности по принципу трансформатора

В результате взаимной индукции во второй катушке возникнет ЭДС взаимоиндукции, равная по величине напряжению, измеряемому вольтметром pV.

Действующее значение этого напряжения зависит от тока I₁:

U₂ = ωMI₁.

Отсюда следует, что взаимная индуктивность

M = . (3.53)

Значит, измерив ток I₁ и напряжение U₂, можно по уравнению (3.53) определить взаимную индуктивность двух катушек.

3.12 Воздушный трансформатор

Трансформатор — это электромагнитный статичный (не имеющий подвижных частей) аппарат, служащий для электрического разделения цепей и для преобразования по величине переменного напряжения.

В простейшем случае трансформатор состоит из двух электрически не связанных неподвижных относительно друг друга и индуктивно-связанных обмоток (рисунок 3.26), расположенных на общем сердечнике.

Рисунок 3.26 — Схема трансформатора

Одну из обмоток с числом витков W₁ подключают к источнику переменного напряжения. Эту обмотку называют первичной и все параметры, связанные с нею, — первичными. Ко второй обмотке (вторичной) с числом витков W₂ подключают нагрузку Z_н.

В первичной обмотке протекает переменный ток i₁, который создает переменный магнитный поток Φ₁, замыкающийся по сердечнику. Пронизывая витки обмоток, этот магнитный поток в соответствии с законом электромагнитной индукции наводит в каждой обмотке соответствующую ЭДС:

– самоиндукции e₁ = — в первичной;

– взаимоиндукции e₂ = — во вторичной.

Как видно, величина этих ЭДС зависит от числа витков. Отношение числа витков первичной и вторичной обмоток называют коэффициентом трансформации.

Если пренебречь падением напряжения внутри обмоток, то возбуждаемые ЭДС E₁ и E₂ уравновешиваются соответствующими напряжениями U₁ и U₂.

Таким образом, эти напряжения также зависят от числа витков. Коэффициент трансформации можно представить отношением первичного U₁ и вторичного U₂ напряжений:

.

Если k > 1, тогда первичное напряжение U₁ больше вторичного U₂. Такой трансформатор называют понижающим. И наоборот, если k < 1, то трансформатор повышающий. В силовых трансформаторах для создания более интенсивного магнитного поля в качестве сердечников используют ферромагнитные материалы.

В ряде случаев в измерительной технике при высоких частотах в трансформаторах используются неферромагнитные сердечники (воздушные трансформаторы). Схема замещения такого трансформатора представлена на рисунке 3.27.

При указанных на схеме (рисунок 3.27) направлениях токов катушки включены согласно. На основании второго закона Кирхгофа запишем уравнения для первичного и вторичного контуров:

; (3.54)

. (3.55)

Рисунок 3.27 — Схема замещения воздушного трансформатора

Совместное решение уравнений (3.54) и (3.55) позволяет определить токи.

Из уравнения (3.55):

. (3.56)

Подставим полученное выражение для тока (3.56) в уравнение (3.54):

.

После преобразования получим:

. (3.57)

Разделим все составляющие уравнения (3.37) на величину тока :

, (3.58)

где Z_вх — комплексное входное сопротивление трансформатора;

— вносимое сопротивление, которое учитывает влияние вторичной обмотки на первичную, т.е. такое сопротивление, которое необходимо внести в первичную цепь, чтобы учесть влияние нагрузки на ток в первичной обмотке.

Если сопротивление нагрузки Z_н = ∞, что равносильно разомкнутым зажимам вторичной обмотки, то трансформатор работает в режиме холостого хода. В этом случае вторичная обмотка не влияет на ток в первичной. Снижение сопротивления нагрузки вызовет увеличение тока в первичной обмотке.

Предположим, что нагрузка подключена к идеальному трансформатору, которому приписывают следующее свойство: при любых сопротивлениях нагрузки отношение первичного и вторичного комплексных напряжений и отношение вторичного и первичного комплексных токов равны друг другу:

.

Входное сопротивление такого трансформатора

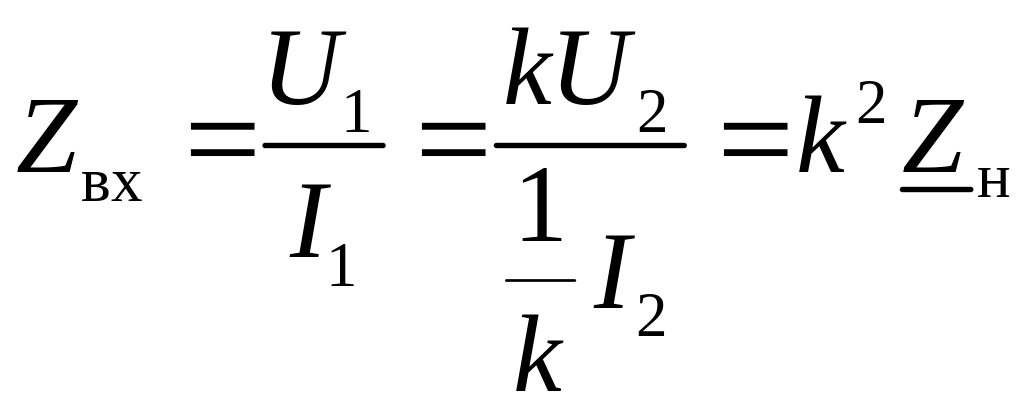, (3.59)

где — сопротивление нагрузки.

Из уравнения (3.59) следует, что в идеальном трансформаторе входное сопротивление больше сопротивления нагрузки на величину квадрата коэффициента трансформации.

Это свойство практически используется в различных областях электротехники, проводной связи, радиотехнике и т.д. для уравнивания сопротивления источника и нагрузки с целью повышения отдаваемой мощности. Поэтому в том случае, когда требуется изменить сопротивление какой-либо нагрузки без изменения самой нагрузки, включается промежуточный трансформатор, по свойствам близкий к идеальному, с коэффициентом трансформации k =  , где Z_вх — требуемое входное сопротивление.

Векторная диаграмма на рисунке 3.28 графически иллюстрирует уравнения (3.54) и (3.55).

Рисунок 3.28 — Векторная диаграмма воздушного трансформатора под нагрузкой

При построении векторной диаграммы принят индуктивный характер нагрузки, т.е. . Направив ток нагрузки по горизонтальной оси, под углом φ_н в сторону опережения, изобразим вектор . Далее в соответствии с уравнением (3.55) к этому вектору прибавляем вектор падения напряжения , совпадающий по фазе с током , и вектор напряжения самоиндукции , опережающий ток на 90°. Результирующий вектор составит вектор напряжения взаимоиндукции . Дальнейшие построения производим в соответствии с уравнением (3.54). Ток отстает по фазе от вектора на 90°. Вектор падения напряжения совпадает по фазе с током , а вектор напряжения самоиндукции опережает ток на 90°. Аналогично вектор напряжения взаимоиндукции опережает вектор тока на 90°. Сумма этих векторов равна вектору напряжения .

Пример 3.1

Рисунок 3.29 — Схема вариометра

Последовательно вариометру (рисунок 3.29) с параметрами катушек R₁ = 5 Ом, L₁ = 0,03 Гн, R₂ = 5 Ом и L₂ = 0,1 Гн подключен приемник с сопротивлением R_н = 3 Ом и X = 30 Ом. Максимальная взаимная индуктивность катушек вариометра Гн. Угловая частота и напряжение источника питания цепи ω = 1000 рад/с, U = 100 В.

Найти пределы изменения напряжения на приемнике U_H при изменении взаимного положения катушек вариометра.

Решение

Напряжение на приемнике U_H можно определить после расчета тока в цепи I.

Изменяя взаимное расположение катушек вариометра можно изменять взаимную индуктивность от M = 0,05 Гн при встречном включении и до M = 0,05 Гн при согласном включении.

С учетом встречного включения катушек уравнение, составленное по второму закону Кирхгофа для контура цепи при обходе контура по часовой стрелке, примет вид:

.

Откуда следует, что ток

.

Пусть начальная фаза напряжения источника φ_и = 0, тогда комплекс напряжения В.

А.

Напряжение на нагрузке

= 2,5(30 – j30) = 75 – j75 В.

Действующее значение напряжения:

В.

При согласном включении уравнение, составленное по второму закону Кирхгофа, примет вид:

.

Откуда следует, что ток

А.

Напряжение на нагрузке

= (0,096 – j0,48)(30 – j30) = –11,52 – j17,28 В.

Действующее значение напряжения

В.

Таким образом, изменяя взаимное расположение катушек вариометра можно изменять напряжение на нагрузке от 106 до 20,8 В.