3.5 Частотные характеристики параллельного контура

Согласно закону Ома ток в неразветвленной части цепи (рисунок 3.6) определяется как:

,

а так как b_L и b_C — это реактивные проводимости ветвей и они зависят от частоты напряжения источника, то и для параллельного контура имеют место частотные характеристики и резонансные кривые.

Пусть имеем цепь (рисунок 3.8) параллельного соединения идеального конденсатора и идеальной катушки, т.е. R₁ = R₂ = 0, подключенную к источнику синусоидального напряжения и неизменным напряжением U.

Рисунок 3.8 — Цепь с параллельным соединением L, C

В такой цепи активные проводимости ветвей равны нулю, емкостная проводимость b_C = ωC, а индуктивная проводимость b_L = . Исходя из этого, частотные характеристики для данной цепи примут вид, представленный на рисунке 3.9.

Резонансные кривые для идеального параллельного контура представлены на рисунке 3.10.

Рисунок 3.9 — Частотные характеристики параллельного контура

Рисунок 3.10 — Резонансные кривые параллельного идеального контура

Если при неизменном действующем значении напряжения источника изменять частоту от 0 до ∞, то при ω = 0 ток в ветви с индуктивностью I₁ будет равен бесконечности, а ток в ветви с емкостью I₂ будет равен 0. По мере увеличения частоты ω ток в индуктивности уменьшается, так как уменьшается индуктивная проводимость, а ток в емкости увеличивается с увеличением емкостной проводимости, при этом пока  > ωC, результирующий ток уменьшается и отстает от напряжения на 90° (φ > 0). Когда частота достигает такой величины, что  = ωC или ω =   = ω₀, то токи в обеих ветвях будут равны: , — а ток I равен нулю. При дальнейшем увеличении частоты ток в ветви с емкостью I₂ будет превышать ток в ветви с индуктивностью. Результирующий ток будет увеличиваться и опережать напряжение на 90°, и при ω = ∞ ток в ветви с индуктивностью будет равен нулю, а ток в ветви с емкостью и результирующий ток будут бесконечно велики.

В общем случае, когда сопротивления ветвей R₁ и R₂ не равны нулю (рисунок 3.6) входная активная проводимость не равна нулю при любой частоте, в связи с чем ток ни при одном значении частоты не достигнет нуля.

При условии, что R₁ < ρ и R₂ < ρ, ток I будет иметь минимальное значение, причем при частоте, отличной от резонансной. Это объясняется тем, что минимальный ток наблюдается при максимальном входном сопротивлении, при частоте, для которой  = 0, а резонанс имеет место при частоте, для которой результирующая реактивная проводимость или результирующее входное сопротивление будут равны нулю.

Не приводя соответствующий анализ, можно сказать, что чем меньше активные сопротивления ветвей, тем меньше входной ток, тем ближе значение частоты при минимальном токе к резонансной частоте.

При условии R₁ = R₂ = ρ, как было указано выше, входное сопротивление не зависит от частоты, и характеристика тока от частоты будет представлять собой прямую, параллельную оси абсцисс.

3.6 Компенсация сдвига фаз

Компенсацией сдвига фаз называется уменьшение угла сдвига по фазе между током и напряжением на входе приемника. В большинстве своем приемники носят активно-индуктивный характер, поэтому уменьшения угла сдвига по фазе можно достичь путем параллельного включения к приемнику конденсатора.

Представим активно-индуктивный электроприемник схемой последовательного включения элементов и (рисунок 3.11, а). На векторной диаграмме (рисунок 3.11, б) вектор тока приемника составляет с вектором напряжения угол . При отсутствии емкости C, включенной параллельно с приемником, ток в линии равен току приемника . При подключении емкости C появится ток , который является практически чисто реактивным, опережающим напряжение на (рисунок 3.11, б). Этот ток компенсирует реактивную составляющую тока приемника , в результате чего реактивная составляющая тока уменьшается, что приводит к уменьшению тока линии .

a) б)

Рисунок 3.11 — Электрическая цепь компенсации сдвига фаз: а — схема; б — векторная диаграмма

, или ,

где — активная составляющая тока нагрузки;

— индуктивная составляющая тока нагрузки.

Угол сдвига фаз между напряжением U и током уменьшается, коэффициент мощности увеличивается.

ЗАПОМНИТЕ:

Повышение коэффициента мощности имеет важное экономическое значение. Так как ток в линии , то при неизменных активной мощности P_н = const и напряжении источника U = const с увеличением коэффициента мощности cosφ уменьшается ток линии, а это приведет к уменьшению потерь мощности в линии , где R_л — активное сопротивление проводов линии (см. пример 3.3). Каждому предприятию задают средневзвешенное значение коэффициента мощности, которое должно быть обеспечено. Самым эффективным способом достижения этой цели наряду с другими и является параллельное подключение конденсаторов. В этом случае энергия в магнитном поле приемника частично или полностью накапливается за счет энергии электрического поля конденсатора, и наоборот, а генератор и провода линии разгружаются от обменной энергии, что позволяет лучше использовать установленную мощность, т.е. увеличить активную мощность, развиваемую генераторами.

С увеличением емкости ток конденсатора I_C = ωCU увеличивается так, что при некоторой емкости он может стать равным индуктивной составляющей тока I_LH (режим резонанса тока). В этом случае произойдет полная компенсация сдвига фаз. Ток линии будет минимальным, равным активной составляющей тока приемника I_aH. При дальнейшем увеличении емкости I_C станет больше I_LH, что приведет к росту тока линии. Наступает режим перекомпенсации. На рисунке 3.12 показано, как изменяется ток линии I_л и cosφ при изменении параллельно подключаемой емкости конденсатора C при P_н = const и U = const. Здесь C_n — емкость полной компенсации.

Для обеспечения заданного значения коэффициента мощности необходимо рассчитать требуемую емкость конденсатора. Если электроприемники имеют мощность P = const и коэффициент мощности cosφ₁, то их реактивная индуктивная мощность Q₁ = Ptgφ₁. При заданном значении cosφ₂ (cosφ₂ > cosφ₁) реактивная мощность должна быть Q₂ = Ptgφ₂.

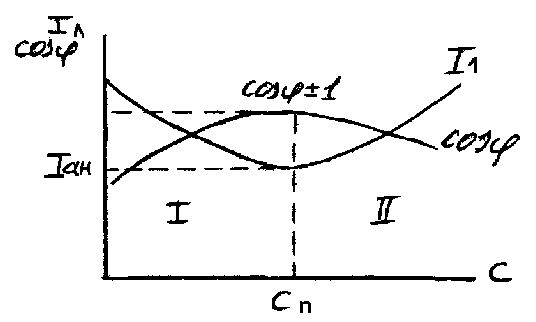
Рисунок 3.12 — Зависимость тока линии и коэффициента мощности от емкости: I — область недокомпенсации; II — область перекомпенсации

Разность реактивных мощностей Q₁ – Q₂ компенсируется емкостной реактивной мощностью конденсаторов:

Q_C = Q₁ – Q₂ = P(tgφ₁ – tgφ₂). (3.19)

Реактивную мощность конденсаторов можно также определить по формуле:

Q_C = b_CU² = ωCU². (3.20)

Приравнивая правые части уравнений (3.19) и (3.20), определяем емкость конденсаторов:

. (3.21)

Подключение конденсаторов для компенсации сдвига фаз осуществляется в месте ввода линии питания в распределительном устройстве. Экономически выгодно, как следует из формулы (3.21), подключать конденсаторы на возможно более высокое напряжение. Угол сдвига фаз обычно доводят до величины, при которой .