2.9.2 Топологические матрицы схем

К топологическим матрицам относят матрицу соединений, или матрицу узлов, контурную матрицу. Составление всех последующих матриц рассматривается на примере схемы электрической цепи (рисунок 2.32, а).

а) б)

Рисунок 2.32 — Схема электрической цепи (а) и ее направленный граф (б)

Для направленного графа составляют таблицу. Число столбцов n в ней полагают равным числу ветвей графа и каждому столбцу присваивают номер ветви. Число строк m в таблице полагают равным числу узлов и каждой строке присваивают номер узла.

Заполняя таблицу, в клетке на пересечении столбца n и строки m записывают «+1», если ветвь n направлена от узла m, «–1», если ветвь n направлена к узлу m. Если ветвь n не соединена с узлом m, то в соответствующей клетке таблицы записывают ноль.

Таблица 2.1 — Таблица для полной узловой матрицы

Узлы		Ветви n
		1	2	3	4	5	6
m	1	0	1	1	1	0	0
	2	–1	–1	0	0	1	0
	3	0	0	–1	0	–1	1
	4	1	0	0	–1	0	–1

Таблицу, заполненную вышеуказанным способом, называют полной узловой матрицей электрической цепи. Ее обозначают символом A₀. Таким образом, полная узловая матрица цепи (рисунок 2.32, а), направленный граф, который изображен на рисунке 2.32, б, имеет вид:

.

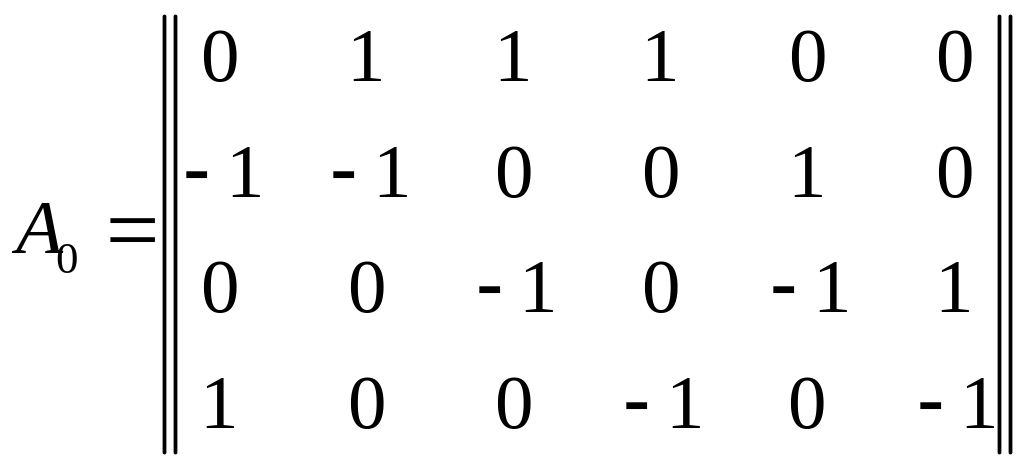Полная узловая матрица определяет схему цепи, т.е. по графу можно составить полную узловую матрицу, и наоборот, по полной узловой матрице можно всегда построить направленный граф. Полная узловая матрица позволяет перевести геометрическую структуру электрической цепи на язык алгебры. Это имеет важное значение при расчетах электрических цепей на ЭВМ.

Если просуммировать элементы столбцов полной узловой матрицы, в результате получают ноль, т.е. в столбце имеются две единицы — +1 и –1, что вытекает из того, что каждая ветвь включена между двумя узлами.

Вследствие этого одна из строк матрицы является зависимой, и полную узловую матрицу можно заменить простой, вычеркнув одну из строк. Такую матрицу называют просто узловой:

.

Перестановка столбцов или строк соответствует лишь изменению нумерации ветвей и узлов, но не меняет схему электрической цепи.

Имея граф электрической цепи (рисунок 2.32, б), выделим одно из его деревьев.

Ветви 1, 5, 6 (рисунок 2.33) являются ветвями связи. Как ранее указывалось, добавление к дереву одной главной ветви образует замкнутый контур. Образуем главные контуры путем добавления ветвей связи. Число главных контуров равно числу ветвей связи. Все они независимы, так как образованы ветвями, ранее не входившими в предыдущий контур.

Примем для каждого контура направление обхода по часовой стрелке (рисунок 2.33).

Рисунок 2.33 — Дерево графа с ветвями связи

Составляют таблицу так, чтобы число строк было равно числу независимых контуров, а число столбцов — числу ветвей графа (таблица 2.2).

При заполнении таблицы в клетку таблицы на пересечении k-контура и n-ветви записывают «+1», если направление обхода k-контура совпадает с направлением n-ветви, в противном случае — «–1».

Если n-ветвь не входит в k-контур, записывают ноль.

Таблица 2.2 — Таблица для контурной матрицы

Контур		Ветвь n
		1	2	3	4	5	6
k	1	1	–1	0	1	0	0
	2	0	1	–1	0	1	0
	3	0	0	1	–1	0	1

Таблица 2.2, составленная подобным образом, называется контурной матрицей:

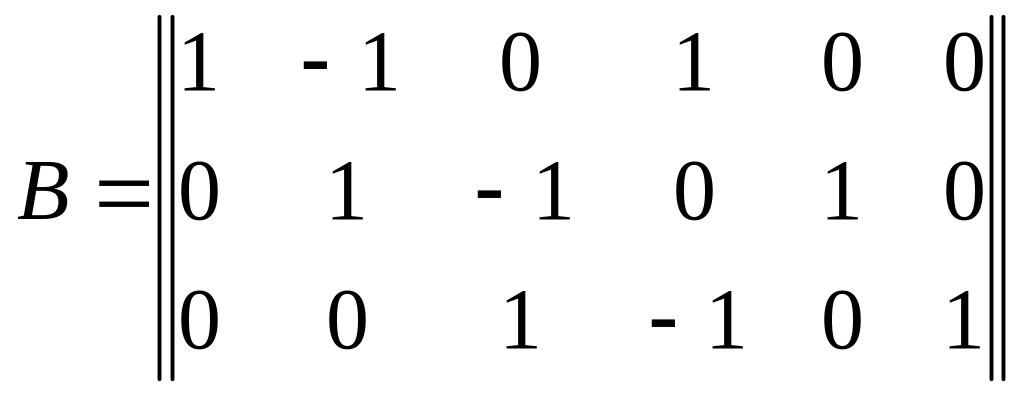
и обозначается B.

Помимо топологических матриц можно составить матрицы параметров ветвей: матрицу ЭДС источников ЭДС, матрицу токов источников токов, матрицу токов ветви, матрицу сопротивлений, матрицу проводимостей.

Матрица ЭДС источников — это столбцовая матрица, число элементов которой равно числу ветвей. Если положительные направления ЭДС источника совпадают с направлением ветви, то соответствующую ЭДС в матрице записывают со знаком «плюс», если не совпадает — со знаком «минус». При отсутствии в ветви источника ЭДС записывают ноль.

Для примера (рисунок 2.32) матрица ЭДС источников ЭДС имеет вид:

.

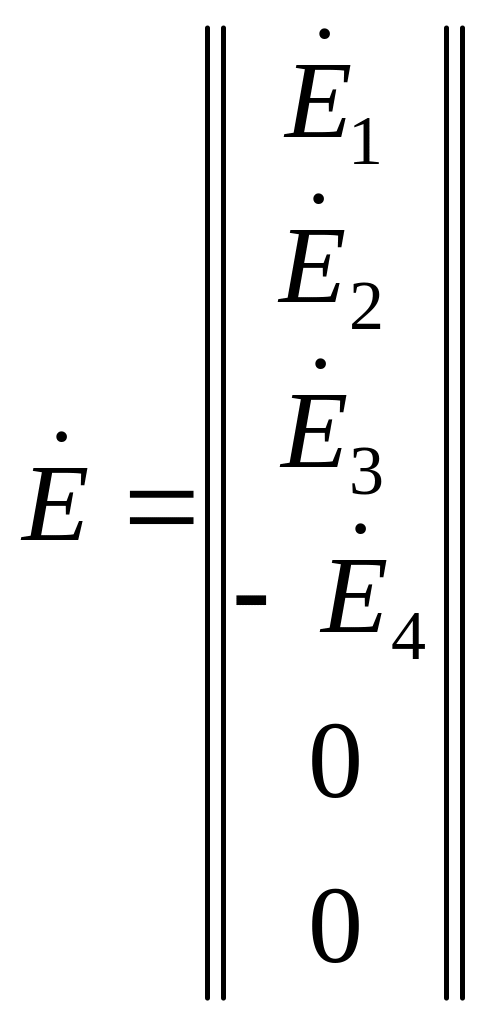Матрица токов источников тока — это столбцовая матрица, где число строк равно числу ветвей графа:

.

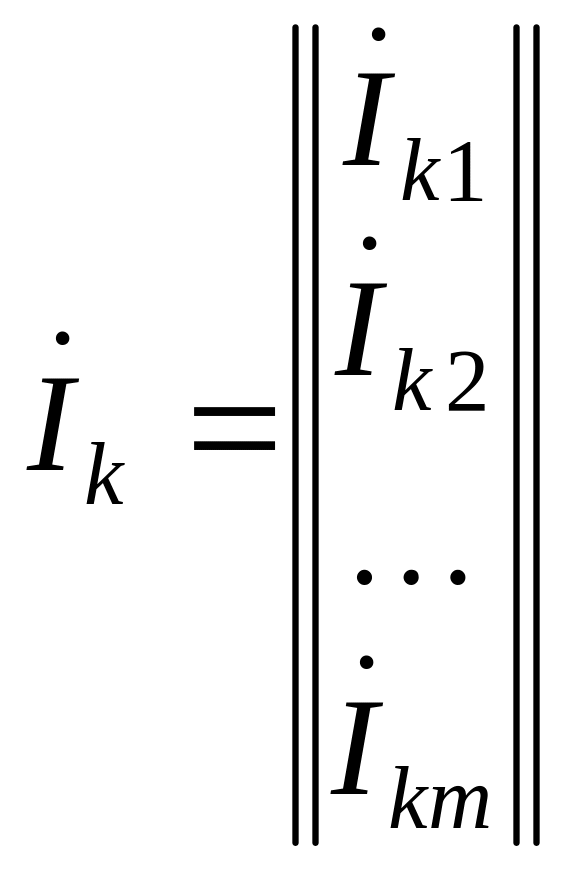Положительное направление тока источника тока должно быть задано и показано на схеме стрелкой. Ток источника в матрице берется со знаком «плюс», если при обходе контура, состоящего из источника и параллельной ему ветви, положительное направление тока источника совпадает с направлением обхода. В противном случае в матрице ток источника тока записывают со знаком «минус».

Матрица токов ветвей — это столбцовая матрица, число строк которой равно числу ветвей:

.

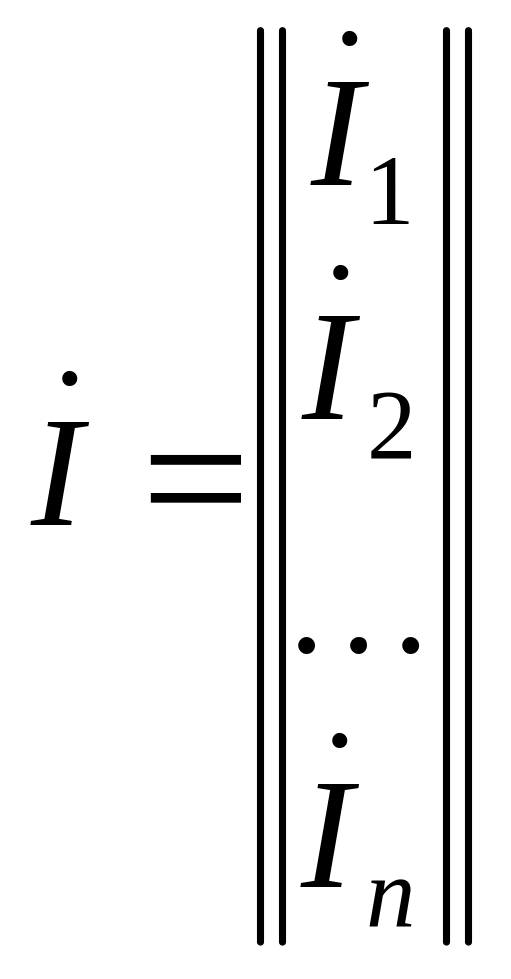Матрица сопротивлений — всегда квадратная. Порядок ее равен числу ветвей. По диагонали матрицы записывают собственные сопротивления ветвей. Если есть взаимные связи (индуктивно связанные катушки), то на пересечении m-строки и n-столбца записывают сопротивление взаимной связи между m и n ветвями.

Если взаимной связи нет (рисунок 2.32), матрица сопротивлений будет диагональной и иметь вид:

.

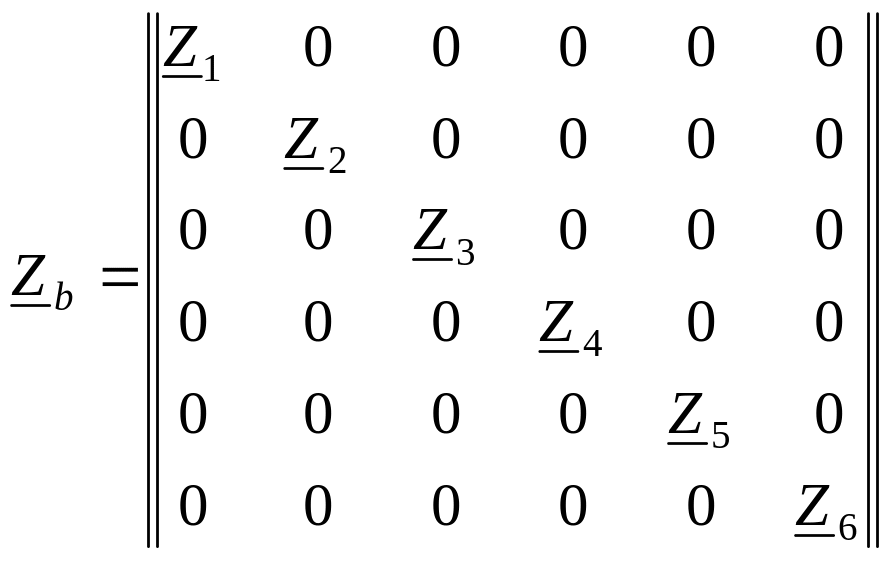Матрица проводимостей — матрица, обратная матрице сопротивлений , т.е. .

При наличии индуктивных связей диагональные и недиагональные элементы матрицы будут отличаться от проводимостей ветвей, так как элементы матрицы не равны обратным значениям элементов матрицы .