
- •Часть 1
- •Содержание
- •Модуль 0 введение в курс теоретических основ электротехники, цели и задачи дисциплины
- •Учебно-информационная модель изучения дисциплины
- •Учебно-информационная модель изучения дисциплины (Окончание)
- •Научно-теоретический материал
- •Модуль 1 основные понятия и законы электрических цепей вводный комментарий к модулю
- •Учебно-информационная модель изучения модуля
- •Учебно-информационная модель изучения модуля (Продолжение)
- •Учебно-информационная модель изучения модуля (Окончание)
- •Словарь основных понятий
- •Основы научно-теоретических знаний по модулю
- •Материалы, используемые в процессе обучения Материалы к лекциям
- •Лекция 1 элементы и параметры электрических цепей
- •1.1 Электрическая цепь. Элементы электрической цепи
- •1.2 Электрическая схема и схемы замещения источников энергии
- •1.3 Ток, напряжение, эдс, мощность, энергия
- •Лекция 2 законы электрических цепей и их применение
- •1.4 Закон Ома для участка цепи, содержащего эдс
- •1.5 Законы Кирхгофа
- •1.6 Энергетический баланс в электрической цепи
- •Лекция 3 основные понятия о цепях синусоидального тока
- •1.7 Общие сведения о цепях переменного тока
- •1.8 Величины, характеризующие синусоидальный ток. Генерирование синусоидальной эдс
- •1.9 Среднее и действующее значения синусоидального тока, напряжения, эдс
- •1.10 Изображение синусоидально изменяющихся величин векторами и комплексными числами. Векторные диаграммы
- •1.11 Синусоидальный ток в активном, индуктивном и емкостном элементах
- •Лекция 4 закон ома, законы кирхгофа для цепи синусоидального тока
- •1.12 Синусоидальный ток в цепи с последовательным соединением активного, индуктивного и емкостного элементов
- •1.13 Закон Ома, законы Кирхгофа для цепей синусоидального тока
- •Лекция 5 энергетические процессы в цепях синусоидального тока
- •1.14 Мгновенная мощность и колебания энергии в цепи синусоидального тока
- •1.15 Активная, реактивная и полная мощности. Баланс мощностей
- •1.16 Условие передачи максимальной активной мощности от источника к приемнику
- •Контрольные вопросы и задачи для самостоятельного изучения цепей постоянного тока
- •Контрольные вопросы и задачи для самостоятельного изучения цепей синусоидального тока
- •Материалы к практическим занятиям
- •Практическое занятие 1 Применение закона Ома для расчета токов и напряжений
- •Практическое занятие 2 Применение законов Кирхгофа для расчета цепей постоянного тока
- •Практическое занятие 3 Применение закона Ома, законов Кирхгофа для расчета цепей синусоидального тока
- •Практическое занятие 4 Электрические цепи переменного тока со смешанным соединением элементов
- •Практическое занятие 5 Мощности в цепях переменного напряжения
- •Материалы к лабораторным занятиям
- •Лабораторное занятие 1 Экспериментальная проверка законов Кирхгофа в цепях постоянного тока
- •Лабораторное занятие 2 Исследование цепи переменного напряжения с последовательным соединением приемников
- •Лабораторное занятие 3 Исследование электрической цепи с параллельным и смешанным соединением элементов
- •Лабораторное занятие № 4 Измерение мощности и определение параметров приемника в цепи переменного тока
- •Материалы к управляемой самостоятельной работе по разделу «Методы расчета простых цепей постоянного тока»
- •Материалы к управляемой самостоятельной работе по разделу «Расчет электрической цепи синусоидального тока со смешанным соединением приемников»
- •Образец контрольных заданий по модулю 1
- •Образец контрольных заданий по модулю 1 (Окончание)
- •Модуль 2 методы расчета электрических цепей вводный комментарий к модулю
- •Учебно-информационная модель изучения модуля
- •Учебно-информационная модель изучения модуля (Окончание)
- •Словарь понятий для повторения
- •Основы научно-теоретических знаний
- •Материалы, используемые в процессе обучения Материалы к лекциям
- •Лекция 1 методы расчета простых электрических цепей и использование при расчете их свойств и преобразований
- •2.1 Расчет простых цепей при последовательном, параллельном и смешанном соединениях приемников
- •2.1.1 Расчет цепи при последовательном
- •2.1.2 Расчет цепи при параллельном соединении приемников
- •2.1.3 Расчет цепи при смешанном соединении приемников
- •2.2 Преобразование соединения «треугольником» в эквивалентное соединение «звездой» и обратно
- •2.3 Использование при расчете свойств электрических цепей
- •Лекция 2 методы расчета сложных электрических цепей
- •2.4 Метод уравнений Кирхгофа
- •2.5 Метод контурных токов
- •2.6 Метод узловых потенциалов
- •2.7 Метод двух узлов
- •2.8 Метод эквивалентного генератора
- •2.9 Матричный метод расчета линейных электрических цепей (для самостоятельной работы)
- •2.9.1 Геометрия электрических цепей
- •2.9.2 Топологические матрицы схем
- •2.9.3 Законы Кирхгофа в матричной форме
- •2.9.4 Закон Ома в матричной форме
- •2.9.5 Матричные уравнения контурных токов
- •2.9.6 Матричные уравнения узловых потенциалов
- •3.9.7 Порядок расчета электрических цепей матричным методом
- •Контрольные вопросы и задачи для самостоятельного решения
- •Материалы к практическим занятиям
- •Практическое занятие 1 Методы расчета сложных электрических цепей (уравнения Кирхгофа, контурных токов, узловых потенциалов)
- •Практическое занятие 2 Методы расчета сложных электрических цепей — 2-х узлов, эквивалентного генератора
- •Практическое занятие 3 Дополнение к методам расчета сложных цепей
- •Материалы к лабораторным занятиям Лабораторное занятие 1 Исследование свойств электрических цепей
- •Материалы к управляемой самостоятельной работе студентов
- •Образец контрольных заданий по модулю 2
- •Образец контрольных заданий по модулю 2 (Окончание)
- •Учебно-информационная модель изучения модуля
- •Учебно-информационная модель изучения модуля (Окончание)
- •Словарь основных понятий
- •Основы научно-теоретических знаний
- •Материалы, используемые в процессе обучения Материалы к лекциям
- •Лекция 1 резонансные явления в электрических цепях
- •3.1 Основные понятия о резонансе в электрических цепях
- •3.2 Резонанс напряжений
- •3.3 Частотные характеристики последовательного колебательного контура
- •3.4 Резонанс токов
- •3.5 Частотные характеристики параллельного контура
- •3.6 Компенсация сдвига фаз
- •3.7 Понятие о резонансе в разветвленных электрических цепях
- •Контрольные вопросы и задачи для самостоятельной работы
- •Вопросы для самоконтроля
- •Лекция 2 цепи со взаимной индуктивностью
- •3.8 Индуктивно-связанные элементы цепи
- •3.9 Электродвижущая сила взаимной индукции
- •3.10 Расчет электрических цепей при наличии индуктивно-связанных элементов
- •3.10.1 Последовательное соединение двух индуктивно-связанных катушек
- •3.10.2 Параллельное соединение двух индуктивно-связанных катушек
- •3.11 Опытное определение взаимной индуктивности
- •3.12 Воздушный трансформатор
- •Контрольные вопросы и задачи для самостоятельного решения
- •Лекция 3 несинусоидальные периодические эдс, напряжения и токи Общие сведения
- •3.12 Разложение периодической несинусоидальной кривой в тригонометрический ряд
- •3.13 Расчет мгновенных значений напряжений и токов в электрических цепях при действии периодических несинусоидальных эдс
- •3.14 Действующие значения периодических несинусоидальных токов, напряжений и эдс
- •3.15 Мощность в цепи несинусоидального тока
- •3.16 Замена несинусоидальных токов и напряжений эквивалентными синусоидальными
- •3.17 Зависимость формы кривой тока от характера цепи при несинусоидальном напряжении
- •Лекция 4 четырехполюсники
- •3.19 Четырехполюсники и их уравнения
- •3.20 Экспериментальное определение коэффициентов четырехполюсника
- •1. Опыт холостого хода при питании со стороны зажимов 1 и 1', . Зажимы 2 и 2' разомкнуты.
- •2. Опыт короткого замыкания при питании со стороны зажимов 1 и 1', . Зажимы 2 и 2' замкнуты накоротко.
- •3. Опыт короткого замыкания при питании со стороны зажимов 2 и 2', . Зажимы 1 и 1' замкнуты накоротко.
- •3.21 Эквивалентные схемы четырехполюсника
- •3.22 Характеристическое сопротивление и коэффициент передачи четырехполюсника
- •3.23 Электрические фильтры
- •Материалы к практическим занятиям
- •Практическое занятие 1 Резонанс в электрических цепях
- •Задачи для самостоятельного решения
- •Индивидуальные задания
- •Практическое занятие 2 Индуктивно-связанные цепи
- •Практическое занятие 3 Цепи с несинусоидальными токами
- •Практическое занятие 4 Мощность в цепи несинусоидального тока
- •Практическое занятие 5 Четырехполюсники
- •Материалы к лабораторным занятиям Лабораторная работа 1 Резонанс токов и компенсация сдвига фаз
- •Лабораторная работа № 2 Исследование режимов работы четырехполюсника
- •Материалы к управляемой самостоятельной работе студентов
- •Образец контрольных заданий по модулю 3
- •Образец контрольных заданий по модулю 3 (Окончание)
- •Задание для усрс
- •Литература Основная
- •Дополнительная
- •Теоретические основы электротехники
- •Часть 1
- •220023, Г. Минск, пр. Независимости, 99, к. 2.
Лекция 2 методы расчета сложных электрических цепей
2.4 Метод уравнений Кирхгофа
Метод уравнений Кирхгофа является универсальным, т.е. пригодным для задач анализа любой электрической цепи. Положим, что в схеме, содержащей B ветвей и Y узлов, заданными являются источники ЭДС и сопротивления приемников, а искомыми — токи в ветвях. Следовательно, число неизвестных равно числу ветвей, и для их нахождения необходимо иметь систему уравнений, составленных по первому и второму законам Кирхгофа.
По первому закону Кирхгофа, выражающему равенство нулю алгебраической суммы комплексных или мгновенных токов в узле, можно записать Y – 1 независимых уравнений.
По второму закону Кирхгофа, выражающему равенство алгебраической суммы комплексных или мгновенных ЭДС в контуре алгебраической сумме комплексных или мгновенных падений напряжений в нем, можно записать B – Y + 1 независимых уравнений.
Система, состоящая из взаимно независимых Y – 1 уравнений по первому закону Кирхгофа и B – Y + 1 уравнений по второму закону в сумме дает необходимое и достаточное число уравнений для определения токов во всех ветвях.
При записи уравнений по второму закону Кирхгофа следует обращать внимание на то, чтобы составленные уравнения были взаимно независимыми. Контуры выбирают так, чтобы в них вошли все ветви схемы, исключая лишь ветви с источниками тока, а в каждом из контуров — возможно меньшее число ветвей. Контуры взаимно независимы, если каждый последующий контур, для которого составляется уравнение, имеет не меньше одной новой ветви и не получается из контуров, для которых уже написаны уравнения, путем удаления из этих контуров общих ветвей.
При составлении уравнений рекомендуется придерживаться такой последовательности: сначала выбрать произвольные положительные направления токов во всех ветвях электрической цепи, затем составить уравнения для узлов на основании первого закона Кирхгофа и уравнения для контуров на основании второго закона Кирхгофа.
В качестве примера запишем систему уравнений по законам Кирхгофа для цепи, схема которой представлена на рисунке 2.15.

Рисунок 2.15 — Схема сложной электрической цепи с источником тока
Так как цепь содержит источник тока, значит ток в этой ветви известен. Следовательно, число неизвестных токов равно трем. Схема содержит два узла, поэтому по первому закону Кирхгофа необходимо составить одно уравнение, а недостающие — по второму закону Кирхгофа. При этом ток источника тока учитывается только при записи уравнения по первому закону Кирхгофа.
В итоге система уравнений имеет вид:
![]() .
.
Подставив в систему
уравнений заданные величины
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
,
и решив ее известными методами, получают
значения токов в ветвях
,
и
.
Результаты расчетов проверяют по первому
закону Кирхгофа.
,
,
,
и решив ее известными методами, получают
значения токов в ветвях
,
и
.
Результаты расчетов проверяют по первому
закону Кирхгофа.
Пример. Определить токи в ветвях сложной цепи (рисунок 2.16) методом уравнений Кирхгофа, если R1 = R2 = 5 Ом; XC1 = 5 Ом; XC2 = 10 Ом; XL3 = 10 Ом; E1 = 100 В; E3 = 200 В.
Решение. Воспользуемся методикой расчета, изложенной в п. 2.4.
Выберем положительные направления токов в ветвях и укажем их на схеме (рисунок 2.9).

Рисунок 2.16 — Схема электрической цепи
Так как электрическая цепь содержит два узла и три ветви, то для решения поставленной задачи необходимо составить систему из трех уравнений: одного — по первому закону Кирхгофа и двух — по второму закону Кирхгофа. При составлении уравнений по второму закону Кирхгофа примем направление обхода контуров по часовой стрелке.
Таким образом, получим систему уравнений относительно неизвестных токов в комплексной форме записи:
![]()
Подставив в полученную систему уравнений известные сопротивления и ЭДС, имеем:
![]()
При решении систем уравнений целесообразно использовать стандартные программы на ЭВМ или математические методы. Для примера воспользуемся методом определителей.
Главный определитель составляем из коэффициентов при неизвестных токах:
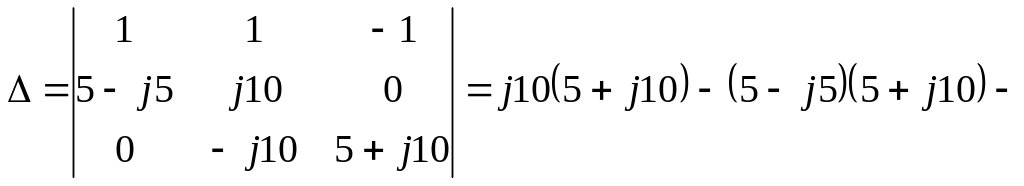
![]() Ом2.
Ом2.
Вспомогательные определители получаем путем замены поочередно одного из столбцов главного определителя на столбец из свободных членов из системы уравнений:
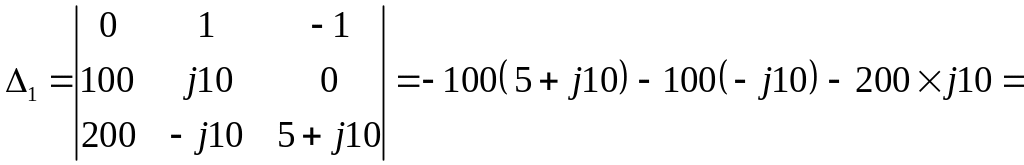
![]() В×Ом2;
В×Ом2;
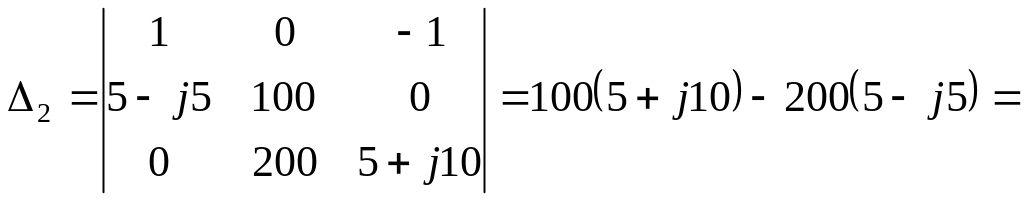
В×Ом2;
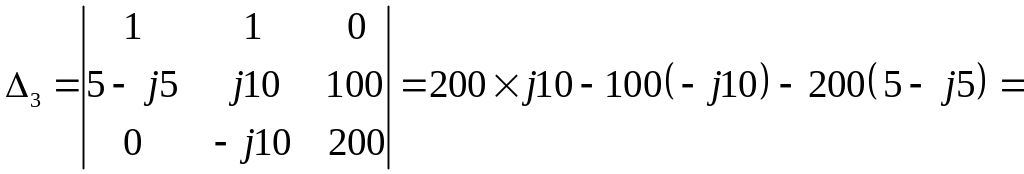
![]() В×Ом2.
В×Ом2.
Тогда искомые токи в комплексной форме:
![]() А;
А;
![]() А;
А;
![]() А.
А.
Действующие значения токов:
![]() А;
А;
![]() А;
А;
![]() А.
А.
Для проверки вычислений используем первый закон Кирхгофа:
![]() ,
или
,
или
![]() .
.
Значит, расчеты выполнены верно.
