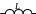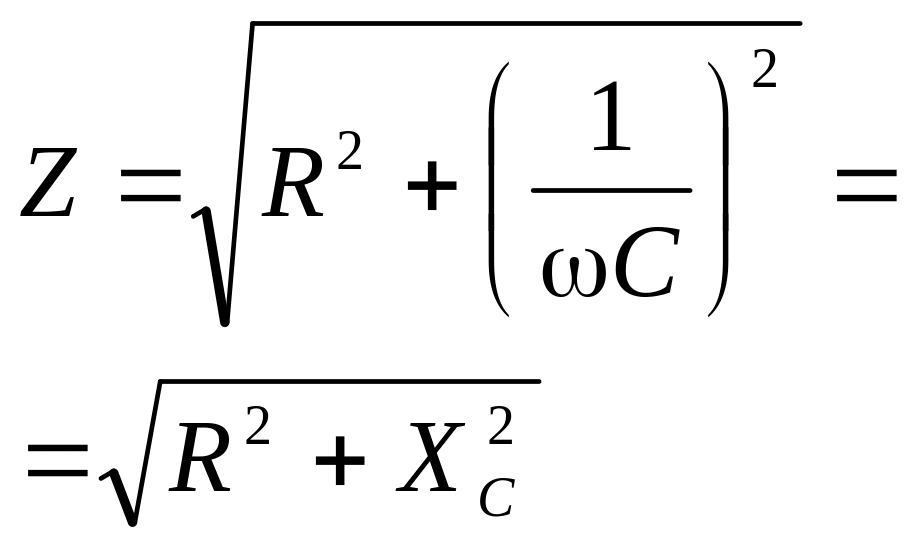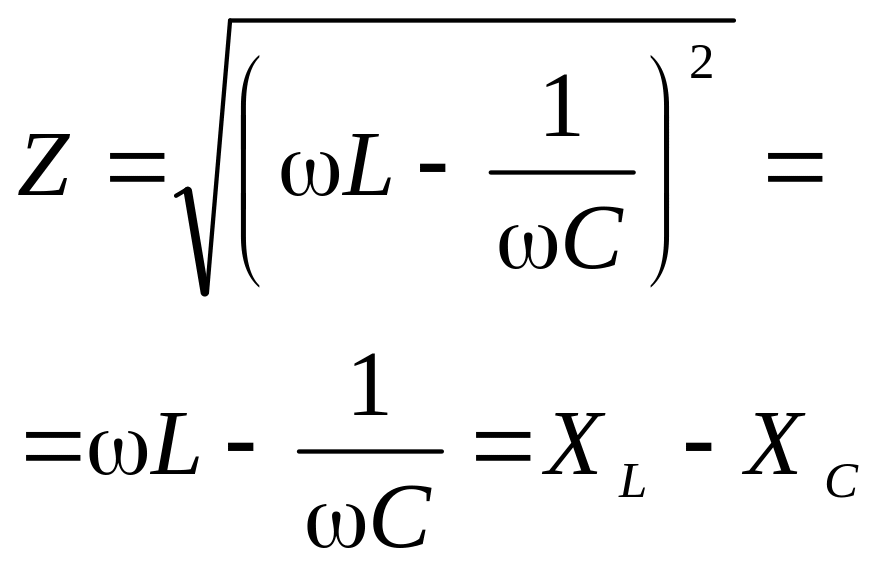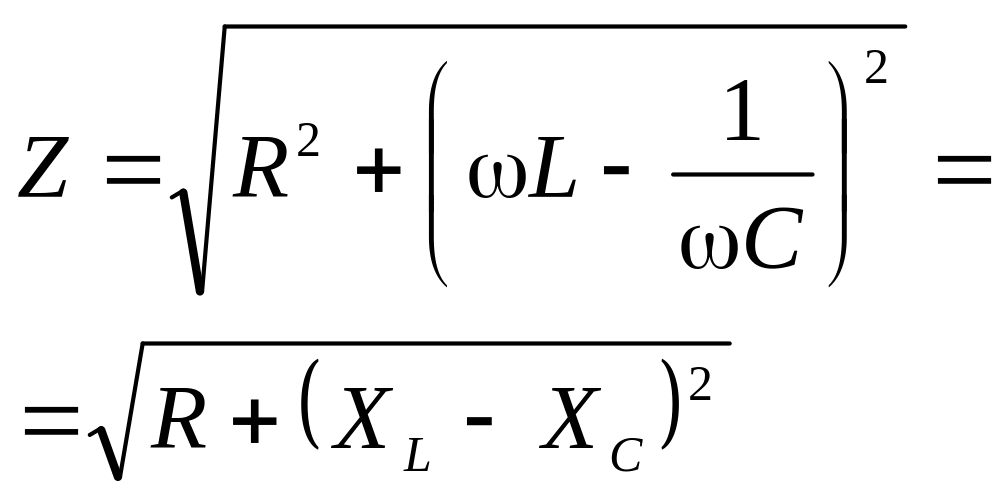- •Часть 1
- •Содержание
- •Модуль 0 введение в курс теоретических основ электротехники, цели и задачи дисциплины
- •Учебно-информационная модель изучения дисциплины
- •Учебно-информационная модель изучения дисциплины (Окончание)
- •Научно-теоретический материал
- •Модуль 1 основные понятия и законы электрических цепей вводный комментарий к модулю
- •Учебно-информационная модель изучения модуля
- •Учебно-информационная модель изучения модуля (Продолжение)
- •Учебно-информационная модель изучения модуля (Окончание)
- •Словарь основных понятий
- •Основы научно-теоретических знаний по модулю
- •Материалы, используемые в процессе обучения Материалы к лекциям
- •Лекция 1 элементы и параметры электрических цепей
- •1.1 Электрическая цепь. Элементы электрической цепи
- •1.2 Электрическая схема и схемы замещения источников энергии
- •1.3 Ток, напряжение, эдс, мощность, энергия
- •Лекция 2 законы электрических цепей и их применение
- •1.4 Закон Ома для участка цепи, содержащего эдс
- •1.5 Законы Кирхгофа
- •1.6 Энергетический баланс в электрической цепи
- •Лекция 3 основные понятия о цепях синусоидального тока
- •1.7 Общие сведения о цепях переменного тока
- •1.8 Величины, характеризующие синусоидальный ток. Генерирование синусоидальной эдс
- •1.9 Среднее и действующее значения синусоидального тока, напряжения, эдс
- •1.10 Изображение синусоидально изменяющихся величин векторами и комплексными числами. Векторные диаграммы
- •1.11 Синусоидальный ток в активном, индуктивном и емкостном элементах
- •Лекция 4 закон ома, законы кирхгофа для цепи синусоидального тока
- •1.12 Синусоидальный ток в цепи с последовательным соединением активного, индуктивного и емкостного элементов
- •1.13 Закон Ома, законы Кирхгофа для цепей синусоидального тока
- •Лекция 5 энергетические процессы в цепях синусоидального тока
- •1.14 Мгновенная мощность и колебания энергии в цепи синусоидального тока
- •1.15 Активная, реактивная и полная мощности. Баланс мощностей
- •1.16 Условие передачи максимальной активной мощности от источника к приемнику
- •Контрольные вопросы и задачи для самостоятельного изучения цепей постоянного тока
- •Контрольные вопросы и задачи для самостоятельного изучения цепей синусоидального тока
- •Материалы к практическим занятиям
- •Практическое занятие 1 Применение закона Ома для расчета токов и напряжений
- •Практическое занятие 2 Применение законов Кирхгофа для расчета цепей постоянного тока
- •Практическое занятие 3 Применение закона Ома, законов Кирхгофа для расчета цепей синусоидального тока
- •Практическое занятие 4 Электрические цепи переменного тока со смешанным соединением элементов
- •Практическое занятие 5 Мощности в цепях переменного напряжения
- •Материалы к лабораторным занятиям
- •Лабораторное занятие 1 Экспериментальная проверка законов Кирхгофа в цепях постоянного тока
- •Лабораторное занятие 2 Исследование цепи переменного напряжения с последовательным соединением приемников
- •Лабораторное занятие 3 Исследование электрической цепи с параллельным и смешанным соединением элементов
- •Лабораторное занятие № 4 Измерение мощности и определение параметров приемника в цепи переменного тока
- •Материалы к управляемой самостоятельной работе по разделу «Методы расчета простых цепей постоянного тока»
- •Материалы к управляемой самостоятельной работе по разделу «Расчет электрической цепи синусоидального тока со смешанным соединением приемников»
- •Образец контрольных заданий по модулю 1
- •Образец контрольных заданий по модулю 1 (Окончание)
- •Модуль 2 методы расчета электрических цепей вводный комментарий к модулю
- •Учебно-информационная модель изучения модуля
- •Учебно-информационная модель изучения модуля (Окончание)
- •Словарь понятий для повторения
- •Основы научно-теоретических знаний
- •Материалы, используемые в процессе обучения Материалы к лекциям
- •Лекция 1 методы расчета простых электрических цепей и использование при расчете их свойств и преобразований
- •2.1 Расчет простых цепей при последовательном, параллельном и смешанном соединениях приемников
- •2.1.1 Расчет цепи при последовательном
- •2.1.2 Расчет цепи при параллельном соединении приемников
- •2.1.3 Расчет цепи при смешанном соединении приемников
- •2.2 Преобразование соединения «треугольником» в эквивалентное соединение «звездой» и обратно
- •2.3 Использование при расчете свойств электрических цепей
- •Лекция 2 методы расчета сложных электрических цепей
- •2.4 Метод уравнений Кирхгофа
- •2.5 Метод контурных токов
- •2.6 Метод узловых потенциалов
- •2.7 Метод двух узлов
- •2.8 Метод эквивалентного генератора
- •2.9 Матричный метод расчета линейных электрических цепей (для самостоятельной работы)
- •2.9.1 Геометрия электрических цепей
- •2.9.2 Топологические матрицы схем
- •2.9.3 Законы Кирхгофа в матричной форме
- •2.9.4 Закон Ома в матричной форме
- •2.9.5 Матричные уравнения контурных токов
- •2.9.6 Матричные уравнения узловых потенциалов
- •3.9.7 Порядок расчета электрических цепей матричным методом
- •Контрольные вопросы и задачи для самостоятельного решения
- •Материалы к практическим занятиям
- •Практическое занятие 1 Методы расчета сложных электрических цепей (уравнения Кирхгофа, контурных токов, узловых потенциалов)
- •Практическое занятие 2 Методы расчета сложных электрических цепей — 2-х узлов, эквивалентного генератора
- •Практическое занятие 3 Дополнение к методам расчета сложных цепей
- •Материалы к лабораторным занятиям Лабораторное занятие 1 Исследование свойств электрических цепей
- •Материалы к управляемой самостоятельной работе студентов
- •Образец контрольных заданий по модулю 2
- •Образец контрольных заданий по модулю 2 (Окончание)
- •Учебно-информационная модель изучения модуля
- •Учебно-информационная модель изучения модуля (Окончание)
- •Словарь основных понятий
- •Основы научно-теоретических знаний
- •Материалы, используемые в процессе обучения Материалы к лекциям
- •Лекция 1 резонансные явления в электрических цепях
- •3.1 Основные понятия о резонансе в электрических цепях
- •3.2 Резонанс напряжений
- •3.3 Частотные характеристики последовательного колебательного контура
- •3.4 Резонанс токов
- •3.5 Частотные характеристики параллельного контура
- •3.6 Компенсация сдвига фаз
- •3.7 Понятие о резонансе в разветвленных электрических цепях
- •Контрольные вопросы и задачи для самостоятельной работы
- •Вопросы для самоконтроля
- •Лекция 2 цепи со взаимной индуктивностью
- •3.8 Индуктивно-связанные элементы цепи
- •3.9 Электродвижущая сила взаимной индукции
- •3.10 Расчет электрических цепей при наличии индуктивно-связанных элементов
- •3.10.1 Последовательное соединение двух индуктивно-связанных катушек
- •3.10.2 Параллельное соединение двух индуктивно-связанных катушек
- •3.11 Опытное определение взаимной индуктивности
- •3.12 Воздушный трансформатор
- •Контрольные вопросы и задачи для самостоятельного решения
- •Лекция 3 несинусоидальные периодические эдс, напряжения и токи Общие сведения
- •3.12 Разложение периодической несинусоидальной кривой в тригонометрический ряд
- •3.13 Расчет мгновенных значений напряжений и токов в электрических цепях при действии периодических несинусоидальных эдс
- •3.14 Действующие значения периодических несинусоидальных токов, напряжений и эдс
- •3.15 Мощность в цепи несинусоидального тока
- •3.16 Замена несинусоидальных токов и напряжений эквивалентными синусоидальными
- •3.17 Зависимость формы кривой тока от характера цепи при несинусоидальном напряжении
- •Лекция 4 четырехполюсники
- •3.19 Четырехполюсники и их уравнения
- •3.20 Экспериментальное определение коэффициентов четырехполюсника
- •1. Опыт холостого хода при питании со стороны зажимов 1 и 1', . Зажимы 2 и 2' разомкнуты.
- •2. Опыт короткого замыкания при питании со стороны зажимов 1 и 1', . Зажимы 2 и 2' замкнуты накоротко.
- •3. Опыт короткого замыкания при питании со стороны зажимов 2 и 2', . Зажимы 1 и 1' замкнуты накоротко.
- •3.21 Эквивалентные схемы четырехполюсника
- •3.22 Характеристическое сопротивление и коэффициент передачи четырехполюсника
- •3.23 Электрические фильтры
- •Материалы к практическим занятиям
- •Практическое занятие 1 Резонанс в электрических цепях
- •Задачи для самостоятельного решения
- •Индивидуальные задания
- •Практическое занятие 2 Индуктивно-связанные цепи
- •Практическое занятие 3 Цепи с несинусоидальными токами
- •Практическое занятие 4 Мощность в цепи несинусоидального тока
- •Практическое занятие 5 Четырехполюсники
- •Материалы к лабораторным занятиям Лабораторная работа 1 Резонанс токов и компенсация сдвига фаз
- •Лабораторная работа № 2 Исследование режимов работы четырехполюсника
- •Материалы к управляемой самостоятельной работе студентов
- •Образец контрольных заданий по модулю 3
- •Образец контрольных заданий по модулю 3 (Окончание)
- •Задание для усрс
- •Литература Основная
- •Дополнительная
- •Теоретические основы электротехники
- •Часть 1
- •220023, Г. Минск, пр. Независимости, 99, к. 2.
Лекция 4 закон ома, законы кирхгофа для цепи синусоидального тока
1.12 Синусоидальный ток в цепи с последовательным соединением активного, индуктивного и емкостного элементов
Пусть в ветви, состоящей из последовательно соединенных активного R, индуктивного L и емкостного C элементов, т.е. в последовательном контуре, или, коротко, RLC-цепи (рисунок 1.34), ток изменяется по синусоидальному закону
i = Imsin(ωt + ψi). (1.57)
На выводах этой цепи создается синусоидальное напряжение, равное алгебраической сумме синусоидальных напряжений на отдельных элементах в соответствии со вторым законом Кирхгофа:
![]() . (1.58)
. (1.58)
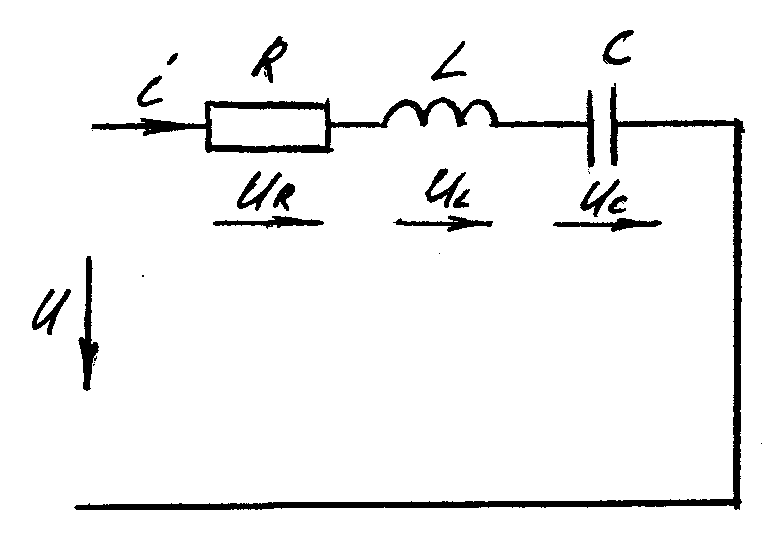
Рисунок 1.34 — Схема последовательного контура
Напряжение uR на сопротивлении R совпадает по фазе с током i:
uR = Ri = RImsin(ωt + ψi). (1.59)
Напряжение uL на индуктивности L опережает ток i на угол π/2:
uL
= L![]() = ωLImcos(ωt
+ ψi)
= ωLImsin(ωt
+ ψi+
), (1.60)
= ωLImcos(ωt
+ ψi)
= ωLImsin(ωt
+ ψi+
), (1.60)
а напряжение uC на емкости C отстает по фазе от тока i на угол π/2:
uC
=
![]() cos(ωt
+ ψi)
=
cos(ωt
+ ψi)
=
![]() sin(ωt
+ ψi+
).
(1.61)
sin(ωt
+ ψi+
).
(1.61)
На рисунке 1.35 показаны мгновенные значения тока в цепи и напряжений на отдельных ее элементах. Здесь имеет место случай, когда начальная фаза тока ψi > 0, а амплитуда напряжения на индуктивности больше амплитуды напряжения на емкости, т.е. индуктивное сопротивление XL больше XC. Как видно, напряжения на емкости и на индуктивности сдвинуты относительно друг друга по фазе на угол π, т.е. находятся в противофазе.

Рисунок 1.35 — Кривая мгновенных значений тока и напряжений в RLC-цепи
В соответствии с (1.58) ординаты кривой напряжения u = Umsin(ωt + ψu) равны алгебраической сумме ординат кривых uR, uL, uC:
Umsin(ωt + ψu)
= RImsin(ωt + ψi)
+ ωLImcos(ωt + ψi)
–
![]() cos(ωt + ψi)=
cos(ωt + ψi)=
= RImsin(ωt + ψi) + (ωL – )Imcos(ωt + ψi). (1.62)
Уравнение (1.62) представляет собой тригонометрическую форму записи второго закона Кирхгофа для мгновенных напряжений. Входящую в него величину
X = XL – XC = ωL – (1.63)
называют реактивным сопротивлением цепи. В зависимости от знака реактивное сопротивление может иметь индуктивный (X > 0) или емкостный (X < 0) характер.
Определение напряжения u сводится к вычислению амплитуды Um и начальной фазы ψu. Для упрощения запишем уравнение (1.62), приняв ψi = 0. Тогда ψu = φ.
Umsin(ωt + φ) = RImsinωt + XImcosωt = Im (Rsinωt + Xcosωt). (1.64)
Воспользовавшись тригонометрическими соотношениями вида:
![]() ;
;
φ = arctg![]() ,
,
получим расчетные выражения для вычисления Um и ψu:
![]() , (1.65)
, (1.65)
φ = arctg![]() . (1.66)
. (1.66)
Соотношение (1.65) аналогично закону Ома. Связь между амплитудными и, соответственно, действующими значениями напряжения и тока в RLC-цепи имеет вид:
![]() ;
;
![]() , (1.67)
, (1.67)
где
![]() ,
(1.68)
,
(1.68)
называют полным сопротивлением цепи.
Активное, реактивное и полное сопротивления относятся к числу основных понятий теории электрических цепей.
Если известно напряжение u = Umsin(ωt + ψu) на выводах RLC-цепи, то ток определяют по формуле:
i
=
![]() sin(ωt
+ ψu
– φ). (1.69)
sin(ωt
+ ψu
– φ). (1.69)
Задача расчета RLC-цепи решается проще комплексным методом.
Представим ток и падения напряжений на всех элементах цепи в комплексном виде, используя выражения их мгновенных значений, и запишем уравнение второго закона Кирхгофа (1.38) в комплексной форме:
![]() , (1.70)
, (1.70)
или
![]() . (1.71)
. (1.71)
Соотношение (1.71) между комплексным напряжением и током называют законом Ома в комплексной форме.
Запишем комплексные величины уравнения (1.70) в показательной форме:
![]() ,
,
где
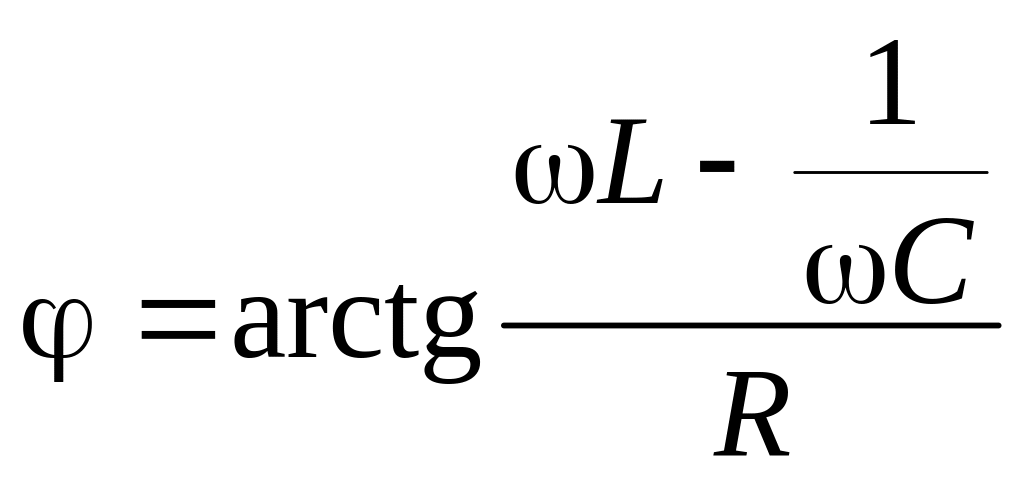 .
.
Комплексные числа равны, если равны их модули и аргументы.
Значит,
U
= I![]() , (1.72)
, (1.72)
ψu = ψi + φ. (1.73)
Уравнение (1.72) представляет собой выражение закона Ома для действующих значений напряжения и тока в цепи.
Так как
![]() и
и
![]() ,
то
,
то
Um = Im . (1.74)
Таким образом,
амплитуда
![]() и начальная фаза ψu
напряжения на выводах RLC-цепи
определены, и можно записать выражение
для мгновенного напряжения:
и начальная фаза ψu
напряжения на выводах RLC-цепи
определены, и можно записать выражение
для мгновенного напряжения:
u = Umsin(ωt + ψi + φ). (1.75)
Векторная диаграмма
RLC-цепи,
построенная в соответствии с уравнением
второго закона Кирхгофа (1.70), представлена
на рисунке 1.36. Первым построен вектор
тока I,
затем совпадающий по фазе с током
вектор напряжения
![]() .
Вектор
.
Вектор
![]() опережает по фазе ток на π/2, а вектор
напряжения
опережает по фазе ток на π/2, а вектор
напряжения
![]() отстает по фазе от тока на угол π/2. Вектор
напряжения
получен как векторная сумма векторов
отстает по фазе от тока на угол π/2. Вектор
напряжения
получен как векторная сумма векторов
![]() ,
и
.
,
и
.
Следует отметить, что уравнения для комплексных напряжений и токов и векторные диаграммы взаимно связаны. Уравнения на основе первого и второго законов Кирхгофа в комплексной форме можно рассматривать как запись геометрических суммирований векторов на векторной диаграмме, и наоборот, векторную диаграмму необходимо рассматривать как графическое представление соотношений между комплексными величинами в уравнении.

Рисунок 1.36 — Векторная диаграмма RLC-цепи
Комплексное сопротивление, треугольник сопротивлений
Отношение комплексного напряжения к комплексному току
 (1.76)
(1.76)
называют комплексным сопротивлением. Для цепи с последовательным соединением R, L, C комплексное сопротивление
Z = R + jωL – j , (1.77)
или в других формах:
![]() , (1.78)
, (1.78)
где R — активное сопротивление (действительная часть комплексного сопротивления);
X — реактивное сопротивление (коэффициент при мнимой части комплексного сопротивления).
Если X = ωL – > 0, то преобладает индуктивное сопротивление, если X < 0, то преобладает емкостное сопротивление.
Очевидно, что полное сопротивление
![]() (1.79)
(1.79)
представляет собой модуль комплексного сопротивления. Аргумент комплексного сопротивления, равный разности начальных фаз напряжения и тока, т.е. φ = ψu – ψi, может быть определен как
φ = arctg![]() . (1.80)
. (1.80)
Расчетные уравнения по определению комплексного и полного сопротивлений при различных схемах участка цепи приведены в таблице 1.2.
Так как модуль
комплексного сопротивления
![]() ,
то на комплексной плоскости Z
можно представить как гипотенузу
прямоугольного треугольника —
треугольника сопротивлений (рисунок
1.37), у которого катетами являются активное
R
и реактивное X
сопротивления.
,
то на комплексной плоскости Z
можно представить как гипотенузу
прямоугольного треугольника —
треугольника сопротивлений (рисунок
1.37), у которого катетами являются активное
R
и реактивное X
сопротивления.
Треугольник сопротивлений представляет собой геометрическую интерпретацию уравнения (1.78). Сопротивление R откладывают на комплексной плоскости в положительном направлении действительной оси, а реактивное сопротивление X в зависимости от его знака откладывают в положительном (рисунок 1.37, а) или отрицательном (рисунок 1.37, б) направлении мнимой оси.
Таблица 1.2 — Примеры расчетных уравнений по определению сопротивлений
Схема участка цепи |
Комплексное сопротивление |
Полное сопротивление |
|
|
|
|
Z = jωL = jXL |
Z = ωL = XL |
|
Z = –j = –jXC |
Z = = XC |
|
Z = R + jωL = = R + jXL |
|
|
Z = R –j = = R –jXC |
|
|
|
|
|
|
|


а) б)
Рисунок 1.37— Треугольник сопротивлений на комплексной плоскости при X > 0 (а) и X < 0 (б)

Рисунок 1.38 — Треугольник сопротивлений
В соответствии с уравнением (1.79) полное сопротивление Z также можно представить как гипотенузу прямоугольного треугольника (рисунок 1.38), у которого катетами являются активное R и реактивное X сопротивления.
Очевидно, что R = Zcosφ и X = Zsincosφ.
Комплексная проводимость, треугольник проводимостей
Комплексной проводимостью называют отношение комплексного тока к комплексному напряжению:
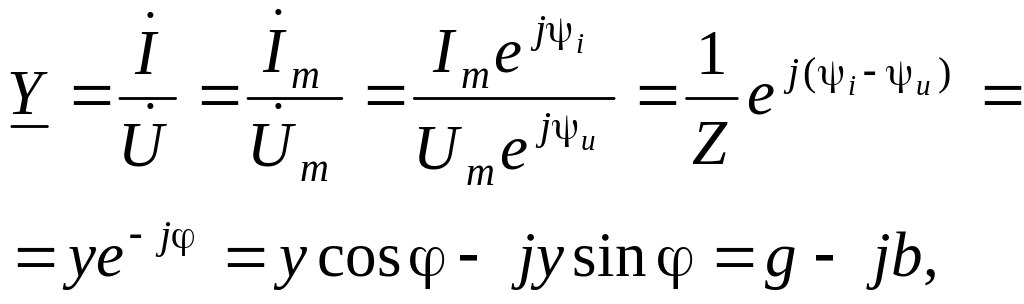 (1.81)
(1.81)
где
![]() — величина, обратная полному сопротивлению,
называется полной
проводимостью.
Комплексная и полная проводимости
измеряются в сименсах (См).
— величина, обратная полному сопротивлению,
называется полной
проводимостью.
Комплексная и полная проводимости
измеряются в сименсах (См).
Комплексная проводимость представляет собой величину, обратную комплексному сопротивлению, что следует из уравнения (1.81). Поэтому ее можно представить иначе:
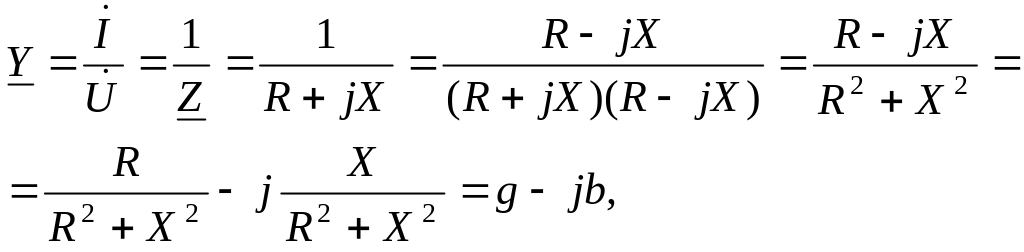 (1.82)
(1.82)
В уравнениях (1.81)
и (1.82)
![]() — действительную часть комплексной
проводимости — называют активной
составляющей
комплексной проводимости, или, короче,
активной
проводимостью.
— действительную часть комплексной
проводимости — называют активной
составляющей
комплексной проводимости, или, короче,
активной
проводимостью.
![]() — коэффициент при
мнимой части, называет реактивной
составляющей
комплексной проводимости, или, короче,
реактивной
проводимостью.
— коэффициент при
мнимой части, называет реактивной
составляющей
комплексной проводимости, или, короче,
реактивной
проводимостью.
Очевидно, что полная проводимость
![]() (1.83)
(1.83)
представляет собой модуль комплексной проводимости. Аргумент комплексной проводимости, равный разности начальных фаз напряжения и тока, т.е. φ = ψu – ψi, может быть также определен по уравнению (1.80).
Треугольник проводимостей (рисунок 1.39) представляет собой геометрическую интерпретацию уравнения (1.81). Активную проводимость g откладывают на комплексной плоскости в положительном направлении действительной оси, а реактивную проводимость b, в зависимости от ее знака, откладывают в отрицательном (рисунок 1.39, а) или положительном (рисунок 1.39, б) направлении мнимой оси.
В соответствии с уравнением (1.83) полную проводимость y также можно представить как гипотенузу прямоугольного треугольника (рисунок 1.40) с катетами g и b.
Очевидно, что
![]() и
и
![]() .
.


а) б)
Рисунок 1.39 —
Треугольник проводимостей на комплексной
плоскости
при
![]() (а)
и
(а)
и
![]() (б)
(б)

Рисунок 1.40 — Треугольник проводимостей