5. Второй закон термодинамики. Эксергия

Второй закон термодинамики определяет направление, в котором протекают процессы, устанавливает условия преобразования тепловой энергии в механическую, а также определяет максимальное значение работы, которая может быть произведена тепловым двигателем.

Математически второй закон термодинамики может быть выражен следующим образом:

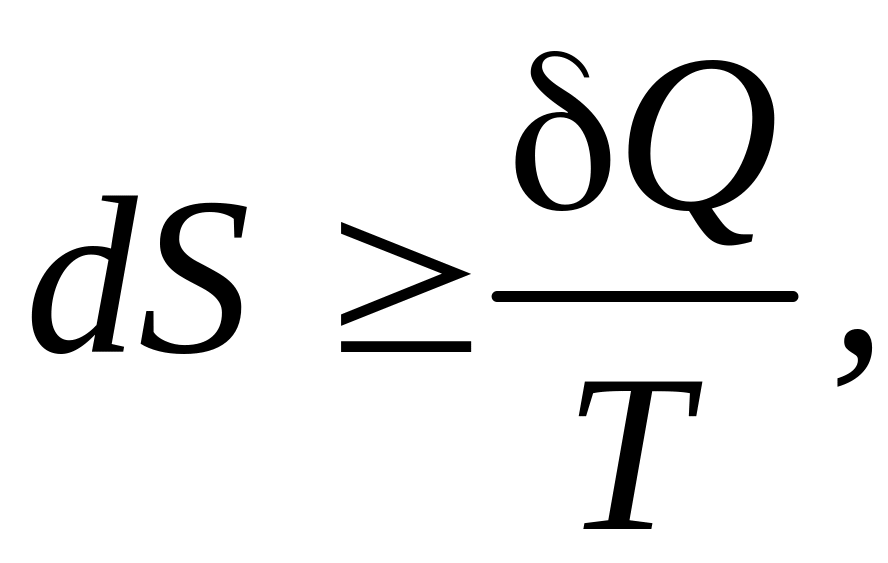(5.1)

где – бесконечно малое приращение энтропии системы;

– бесконечно малое количество теплоты, полученное системой от источника теплоты.

Знак равенства соответствует обратимым процессам, знак неравенства – необратимым. Чем выше степень необратимости процессов, тем сильнее возрастание энтропии.

Первый и второй законы термодинамики для обратимых процессов могут быть записаны совместно в виде термодинамических тождеств:

; (5.2)

. (5.3)

Эксергия системы – это максимальная работа, которую может совершить система при переходе в состояние равновесия с окружающей средой. Эксергетический анализ работы теплоэнергетических и технологических установок учитывает не только количественные, но и качественные характеристики энергоресурсов в различных элементах установок, а также необратимость протекающих в них процессов.

Эксергия тепла термодинамического процесса , Дж находится как

, (5.4)

где Q – теплота термодинамического процесса, Дж;

– изменение энтропии рабочего тела, Дж/К;

Т₀ – температура окружающей среды, К.

Эксергия является экстенсивной функцией состояния, поэтому удельная эксергия тепла , Дж/К определяется как

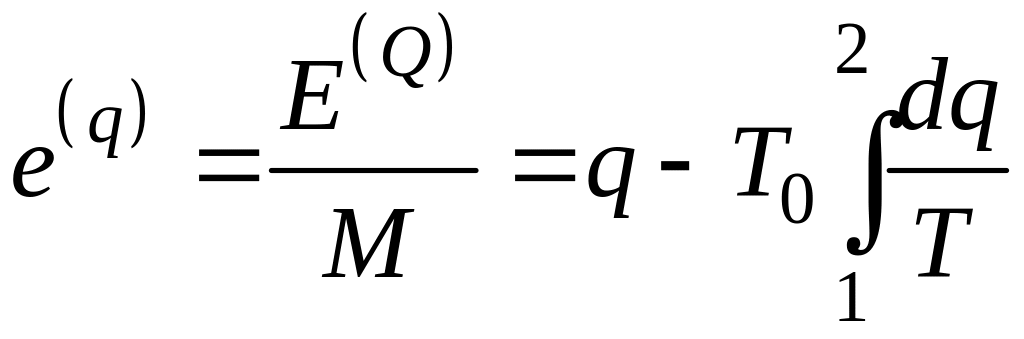. (5.5)

Графически удельная эксергия тепла представлена на рис 5.1. Общая площадь под кривой процесса 1–2 соответствует количеству удельной теплоты процесса q. Она состоит из эксергии тепла процесса (площади, заштрихованной вертикальными линиями) и неработоспособной части тепла (площади, заштрихованной горизонтальными линиями).

Рис. 5.1. Эксергия тепла термодинамического процесса

Потери работоспособности (эксергетические потери) за счет необратимости процессов, протекающих в системе, определяются по формуле Гюи-Стодолы

, (5.6)

где ­– полное приращение энтропии всех подсистем, входящих в данную систему.

Если в исходном состоянии термодинамическая система имеет параметры U, S, V, а в конечном – находится в равновесии с окружающей средой и имеет параметры , то эксергия неподвижной термодинамической системы E определяется как

, (5.7)

а удельная эксергия e неподвижной системы как

, (5.8)

где – параметры окружающей среды.

Для неподвижной системы, совершающей некоторый обратимый процесс 1–2, максимальная работа равна убыли эксергии:

. (5.9)

Тогда для необратимого процесса уравнение баланса эксергии примет вид

, (5.10)

то есть при переходе из состояния 1 в состояние 2 эксергия системы расходуется на совершение работы L, а часть работоспособности теряется из-за необратимости процессов.

При нахождении эксергии потока вещества в форме Лагранжа система координат движется вместе с потоком. Если начальные параметры потока H, S, а конечные соответствуют состоянию равновесия потока с окружающей средой , то выражение для эксергии потока в форме Лагранжа имеет вид

, (5.11)

а для удельной эксергии потока :

. (5.12)

Максимальная внешняя работа совершается за счет убыли эксергии потока

. (5.13)

Эксергетические потери находятся также по формуле Гюи-Стодолы

, (5.14)

тогда уравнение баланса эксергии потока имеет вид

. (5.15)

Задачи

5.1. Вычислить эксергию тепла изобарного процесса нагрева воздуха от температуры 20 ^оС до температуры 900 ^оС, если теплоемкость воздуха с_р = 1 кДж/кг, а температура окружающей среды 15 ^оС.

Решение

Эксергия тепла термодинамического процесса определяется в соответствии с (5.5) как

.

Подставив в это уравнение выражения для количества теплоты и изменения энтропии в изобарном процессе:

,

получим

5.2. Вычислить эксергию потока водяного пара в форме Лагранжа, если водяной пар находится при давлении 50 бар и температуре 500 ^оС. Давление окружающей среды 1 бар, температура 27 ^оС.

Решение

Эксергия потока в форме Лагранжа находится в соответствии с (5.12):

.

Энтальпия и энтропия водяного пара находятся по табл. П.2.2.

– при давлении 50 бар и температуре 500 ^оС:

;

– при параметрах окружающей среды (давлении 1 бар и температуре 27 ^оС):

.

Тогда эксергия потока водяного пара

.

5.3. В регенеративном теплообменнике воздух с начальной температурой 50 ^оС изобарно нагревается дымовыми газами, поступающими в теплообменник с температурой 700 ^оС и изобарно охлаждающимися до температуры 200 ^оС. Расход воздуха 200 кг/с, расход дымовых газов 100 кг/c. Теплоемкости воздуха и дымовых газов 1,0 кДж/(кг∙К) и 1,2 кДж/(кг∙К) соответственно. Температура окружающей среды 27 ^оС. Вычислить эксергии тепла горячего и холодного теплоносителей в теплообменном аппарате, эксергетические потери и эксергетический КПД теплообменного аппарата. Тепловыми потерями пренебречь.

Ответ:

5.4. Вычислить эксергию углекислого газа CO₂, имеющего параметры p = 10 бар, T = 600 К, по отношению к окружающей среде с параметрами p₀ = 1 бар, T₀ = 293 К.

Ответ: е = 98,9 кДж/кг.

5.5. Определить потерю работоспособности воздуха при его дросселировании от давления p₁ = 100 бар до давления p₂ = 50 бар. Температура окружающей среды T₀ = 300 К.

Решение

Потери работоспособности термодинамической системы определяются формулой Гюи–Стодолы (5.6):

.

Поскольку при дросселировании воздуха (идеального газа) температура его не изменяется, то будем иметь в расчете на 1 кг воздуха

5.6. Определить изменение работоспособности при переходе 1 кг азота N₂ из состояния, определяемого давлением p₁ = 10 бар и температурой T₁ = 770 К, в состояние с параметрами p₂ = 2 бар, T₂ = 300 К. Параметры окружающей среды T₀ = 283 К, p_o= 1 бар.

Ответ:

5.7. Определить увеличение энтропии и уменьшение работоспособности при смешении 4 кг водорода H₂ и 1 кг углекислого газа CO₂, находившихся при одинаковых температурах и давлениях, причем полный объем смеси становится равным суммарному объему смешиваемых газов. Температура окружающей среды T₀ = 293 К.

Решение

Формула для энтропии смешения двух различных идеальных газов при одинаковых температурах и давлениях приводится к виду

где – газовая постоянная, – молекулярная масса, – число киломолей.

Подставляя численные данные, получаем

Потери работоспособности

5.8. Как изменится максимальная работоспособность ΔL_max углекислого газа CO₂, содержащегося в жестком теплоизолированном баллоне объемом V = 100 л при давлении p = 150 бар и температуре t = 27 ^оС, при его транспортировке с поверхности Земли на поверхность Венеры?

Параметры атмосферы на поверхности Земли: p_З = 1 бар, t_З = 27 ^оС. Параметры атмосферы на поверхности Венеры: p_В = 90 бар, t_В = 500 ^оС.

Ответ: увеличится на 520,2 кДж.

5.10. Определить максимальную работоспособность (эксергию) Е₁, которую имеют 500 кДж тепла при температуре пламени в котельном агрегате t₁ = 1500 ^оС. Определить, чему будет равна максимальная работоспособность Е₂ того же количества теплоты, когда она будет передана влажному водяному пару в барабане котла при давлении p₂ = 130 бар. Температура окружающей среды t₀ = 20 ^оС.

Ответ: Е₁ = 417,4 кДж, Е₂ = 257,5 кДж.

5.11. В регенеративный теплообменник газотурбинной установки поступает воздух после компрессора с температурой t_в1 = 140 ^оС, где он изобарно нагревается за счет продуктов сгорания, поступающих из турбины с температурой t_г1 = 340 ^оС. В теплообменнике продукты сгорания изобарно охлаждаются до температуры t_г2 = 210 ^оС. Определить потерю работоспособности тепла в регенеративном теплообменнике в результате необратимого теплообмена в расчете на 1 кг рабочего тела. Продукты сгорания обладают свойствами воздуха с постоянной теплоемкостью. Температура окружающей среды t₀ = 20 ^оС. Тепловыми потерями пренебречь.

Ответ: