4. Работа и теплота. Первый закон термодинамики

При взаимодействии термодинамической системы с окружающей средой происходит обмен энергией. Способ передачи энергии, связанный с изменением внешних параметров, называют работой, а без изменения внешних параметров – теплотой.

Работа характеризует упорядоченную форму обмена энергией с окружающей средой, связанную с макроскопическими перемещениями в системе (сжатие, расширение, перемещение в поле сил тяжести и др.).

Работа изменения объема L, Дж, определяется как:

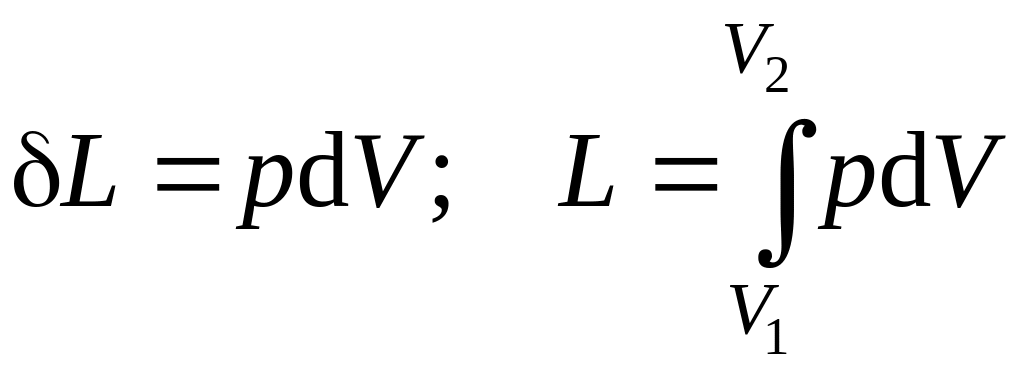. (4.1)

Работа, отнесенная к единице массы системы, называется удельной работой , Дж/кг. Для нее выражения (4.1) принимают вид:

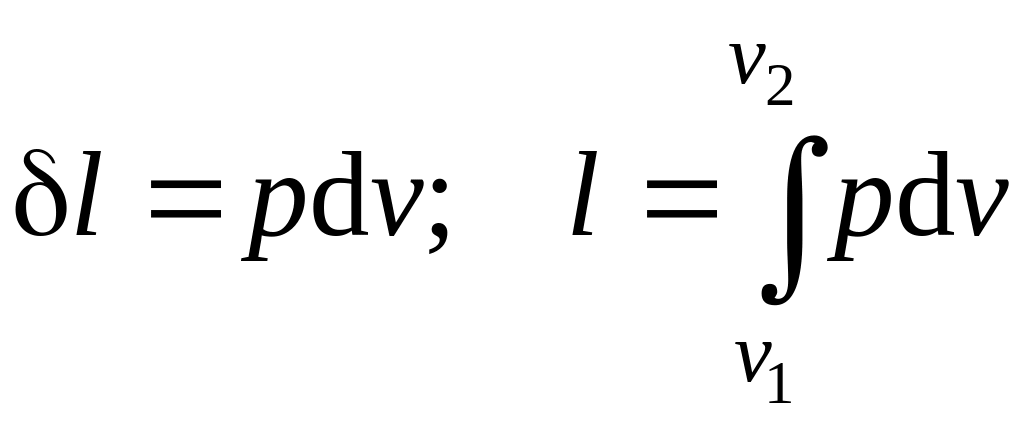. (4.2)

Работа является функцией процесса и графически изображается площадью под кривой процесса (1–2) в диаграмме p–v (рис. 4.1). Работа считается положительной, если она производится системой над внешними телами, и отрицательной, если она совершается над системой.

Теплота характеризует микроскопическую неупорядоченную форму обмена энергией, имеющую место при тепловом контакте тел с различной температурой, и самопроизвольно передается от более нагретого тела к менее нагретому на молекулярном уровне.

Количество теплоты Q, Дж, полученное или отданное системой, равно:

, (4.3)

где – теплоемкость вещества, определяемая по молекулярно-кинетической теории или как средняя теплоемкость в интервале температур , индекс x – определяет характер процесса ( ) (см. разд. 3).

Количество теплоты также можно найти, воспользовавшись вторым законом термодинамики (см. разд. 5):

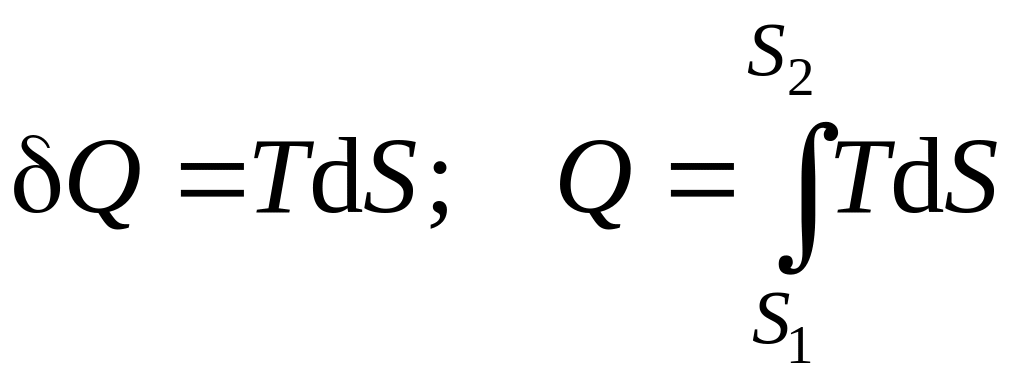, (4.4)

где S, Дж/К – энтропия системы.

Количество теплоты, отнесенное к единице массы системы, называется удельным количеством теплоты 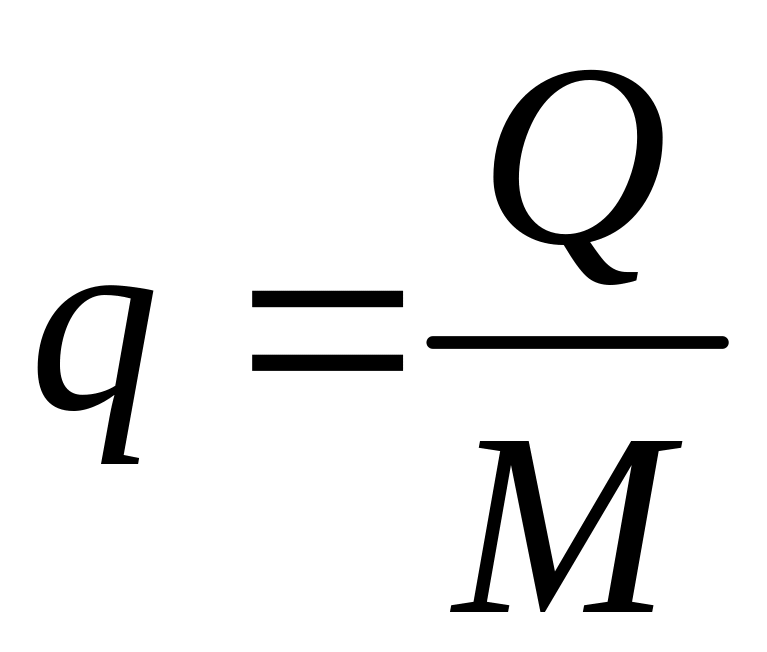, Дж/кг и определяется как:

, (4.5)

или

. (4.6)

Графически теплота изображается площадью под кривой процесса (1–2) в диаграмме T–s (рис. 4.1). Теплота считается положительной, если она подводится к системе (энтропия в процессе подвода тепла увеличивается, ), и отрицательной, если она отводится от системы (энтропия в процессе отвода тепла уменьшается, ).

Рис. 4.1. Графическое изображение работы l,

полезной внешней работы l' и теплоты q

Первый закон термодинамики является законом сохранения и превращения энергии применительно к термодинамическим системам. В соответствии с ним теплота, подведенная к системе, идет на изменение ее внутренней энергии (см. разд. 3) и на совершение ею работы:

(4.7)

или в дифференциальной форме:

. (4.8)

Первый закон термодинамики может быть записан также в терминах энтальпии (см. разд. 3):

. (4.9)

Здесь – полезная внешняя (располагаемая) работа, определяемая как

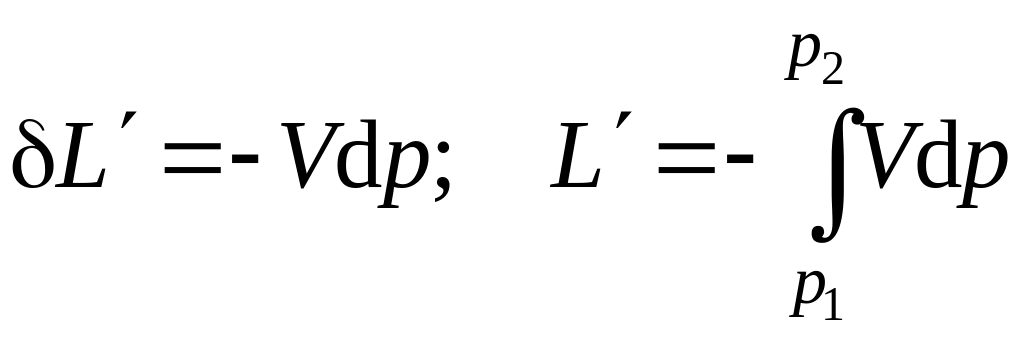, (4.10)

а – удельная внешняя работа,

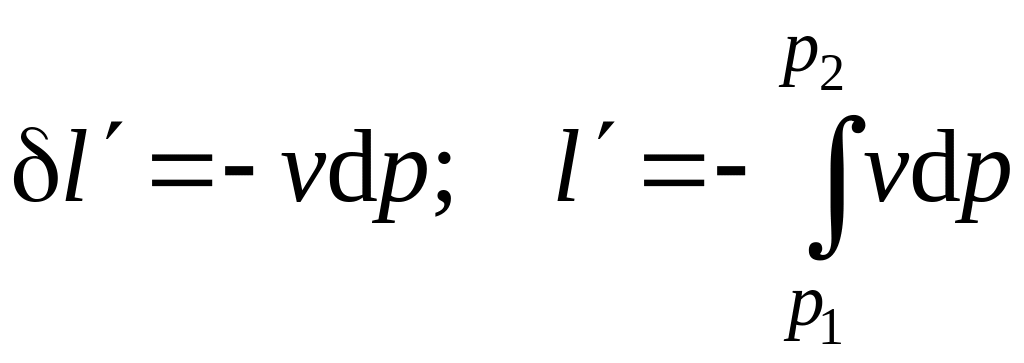. (4.11)

Графически полезная внешняя работа изображается площадью слева от кривой процесса в диаграмме p–v (рис. 4.1).

Задачи

4.1. Навстречу друг другу с одинаковой скоростью летят два одинаковых куска льда. При какой скорости они при неупругом ударе испарятся? Начальная температура кусков льда t₁= –30 ^оС. Теплоемкость льда с_л = 2,1 кДж/(кг∙К), теплота плавления льда r_пл = 333,7 кДж/кг, теплоемкость воды с_в = 4,19 кДж/(кг∙К), теплота парообразования r = 2257 кДж/кг.

Решение

Возрастание внутренней энергии системы двух соударяющихся тел произойдет за счет уменьшения их кинетической энергии. Поскольку тела одинаковые и летят навстречу друг с другом с одинаковыми скоростями, то

.

Теплота, выделяющаяся при ударе, пойдет на нагрев кусков льда до температуры плавления, на сам процесс плавления льда, далее на нагрев образующейся воды до температуры кипения и на испарение воды. Следовательно

.

Отсюда начальная скорость кусков льда

4.2. Сколько килограммов свинца можно нагреть от температуры t₁ = 15 ^оС до температуры его плавления t_пл = 327 ^оС посредством удара молотом массой 200 кг при падении его с высоты 2 м. Вся энергия падения молота превращается в теплоту, целиком поглощаемую свинцом. Теплоемкость свинца с_св = 0,1256 кДж/(кг∙К).

Решение

Поскольку энергия падения молота превращается в теплоту, целиком поглощаемую свинцом, то

,

откуда масса свинца

.

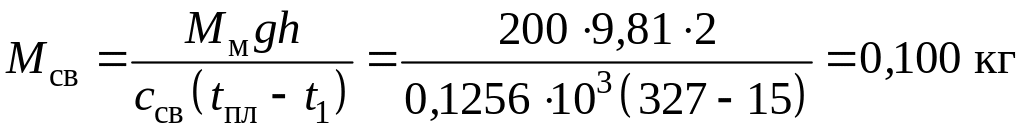4.3. Стальной шарик падает с высоты h₁ = 8,16 м на идеально гладкую горизонтальную плоскость и отскакивает от нее на высоту h₂ = 1 м. На сколько градусов повысится температура шарика после удара, если на его нагревание расходуется 70 % энергии удара? Теплоемкость стали c_ст = 0,46 кДж/(кгК).

Ответ: Δt = 10,7 ^оС.

4.4. Свинцовая пуля пробивает доску, при этом ее скорость падает с 400 м/с до 200 м/с. Какая часть пули расплавится? Нагреванием доски пренебречь. Начальная температура 30 ^оС. Теплота плавления свинца r_пл = 20,934 кДж/кг.

Ответ: 89 %.

4.5. Свинцовый шар массой 200 г, двигающийся без вращения со скоростью 2 м/с, ударил в такой же неподвижный шар, после чего оба шара стали двигаться в одном направлении с одинаковыми скоростями. Насколько возросла их внутренняя энергия при ударе?

Ответ: .

4.6. 1 литр воды нагревается с помощью электрического кипятильника мощностью 300 Вт. За какое время вода нагреется до температуры кипения, если теплообмен с окружающей средой отсутствует, а начальная температура воды равна 20 ^оС.

Ответ: τ = 18,6 мин.

4.7. Какая доля теплоты, подведенной к 1 кг кислорода в изобарном процессе, затрачивается на изменение внутренней энергии?

Ответ: Δu = 0,714q.

4.8. Работа расширения 0,1 кмоля воздуха равна 17 кДж. Определить изменение удельной внутренней энергии системы, если в процессе расширения от воздуха отводится 63 кДж теплоты.

Решение

Согласно первому закону термодинамики , отсюда

.

Примечание: количество теплоты подставляется со знаком «минус», так как теплота от воздуха отводится.

4.9. К газу, заключенному в цилиндре с поршнем, подводится извне 100 кДж теплоты. Величина произведенной при этом работы составляет 115 кДж. Определить изменение удельной внутренней энергии газа, если его количество составляет 0,8 кг.

Ответ: Δu = – 18,75 кДж/кг.

4.10. К 2 кг кислорода подведено 300 кДж тепла. Определить, какое количество теплоты пошло на изменение внутренней энергии и на совершение работы, если в результате термодинамического процесса температура газа возросла от 10 ^оС до 166 ^оС.

Ответ: 67 % – на изменение внутренней энергии, 33 % – на совершение работы.

4.11. Работа расширения 0,5 кг газа составляет 10 кДж. При этом от газа отнимается 10 ккал тепла. Как изменится удельная внутренняя энергия в результате совершения процесса?

Ответ: Δu = – 103,8 кДж/кг.

4.12. При торможении двигателя работа, произведенная двигателем, расходуется на преодоление сил трения и превращается в теплоту, 20 % которой рассеивается в окружающей среде, а остальная часть отводится с охлаждающей водой в тормозной системе. Сколько воды надо подвести к тормозу за 1 час, если крутящий момент на валу , частота вращения n = 1500 об/мин, а допустимое повышение температуры воды .

Теплоемкость воды .

Решение

Так как мощность двигателя целиком переходит в теплоту трения, 80 % которой поглощается водой, то энергетический баланс можно записать в следующем виде:

,

где мощность двигателя

.

Тогда

.

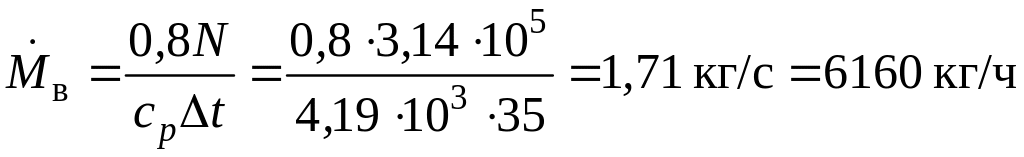4.13. Какое количество охлаждающей воды следует подавать в час на колодки испытательного тормоза, если мощность двигателя 60 кВт, температура охлаждающей воды 20 ^оС, а предельно допустимая температура воды на выходе 80 ^оС?

25 % теплоты трения рассеивается в окружающей среде. Теплоемкость воды .

Ответ: .

4.14. Газ, состояние которого определяется на p-v диаграмме точкой 1 (рис. 4.2), переходит в состояние 2 по пути 1а2. При этом к газу подводится 80 кДж теплоты, а работа, совершенная газом, составляет 30 кДж. Затем газ возвращается в исходное состояние по пути 2b1.

Какое количество теплоты необходимо подвести или отвести в процессе 2b1, если работа, затраченная на сжатие газа в этом процессе, составляет 50 кДж?

Рис. 4.2. К задачам 4.14, 4.15

Решение

Запишем уравнения первого закон термодинамики для процессов 1а2 и 2b1:

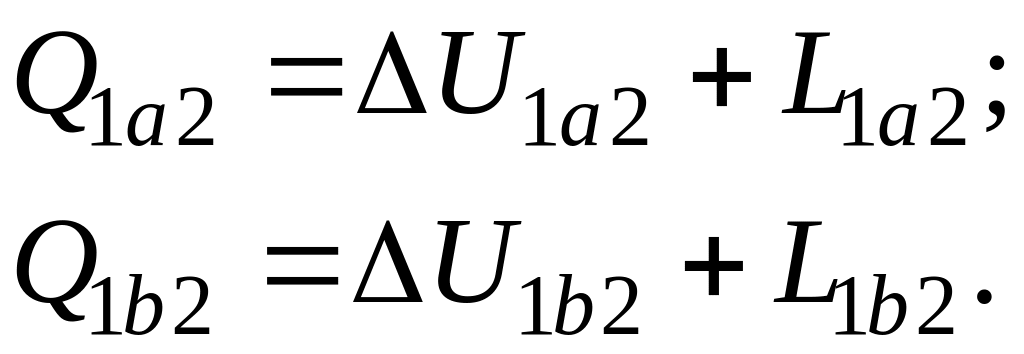
Так как изменение внутренней энергии не зависит от характера процесса, а определяется только параметрами состояния, то

откуда , причем теплота в процессе 2b1отводится (так как ).

4.15. Для условий задачи 4.14 определить, сколько теплоты необходимо подвести к газу в процесс 1с2, чтобы от газа получить работу, равную 10 кДж?

Ответ: .

4.16. Газ может переходить из состояния 1 в состояние 2 по пути 1а2 или по пути 1b2 (рис. 4.3). Насколько будут отличаться количества подведенной и отведенной теплоты в этих процессах, если давления в точках 1 и 2 равны 0,1 МПа и 0,5 МПа соответственно, а изменение объема ?

Рис. 4.3. К задаче 4.15

Ответ: .

4.17. Пассажирский пароход идет со скоростью 20 км/ч. Какова мощность силовой установки парохода, если на 1 км пути расходуется 50 кг каменного угля с теплотой сгорания 5000 ккал/кг? КПД силовой установки 12 %.

Ответ: .

4.18. Какое количество тепла может быть получено от 1 г урана U²³⁵ в атомном реакторе, если для силовой установки мощностью 75000 л.с. требуется 140 г урана в сутки при КПД реактора 40 %? Сколько бы потребовалось в сутки угля с теплотой сгорания 7000 ккал/кг для этой же силовой установки? (1 л.с. = 0,735 кВт).

Ответ:

4.19. Определить КПД двигателя мощностью 50 л.с., если расход бензина на 1 км пути составляет 320 г при скорости 40 км/ч. Теплота сгорания бензина 10500 ккал/кг.

Ответ: .