3. ТеплоЕмкость газов и газовых смесей. Внутренняя энергия и энтальпия идеального газа

Удельной теплоемкостью называется количество теплоты Q, которое необходимо сообщить единице количества вещества, чтобы изменить его температуру на один градус. В зависимости от способа измерения количества вещества различают:

– удельную массовую теплоемкость, Дж/(кг∙К):

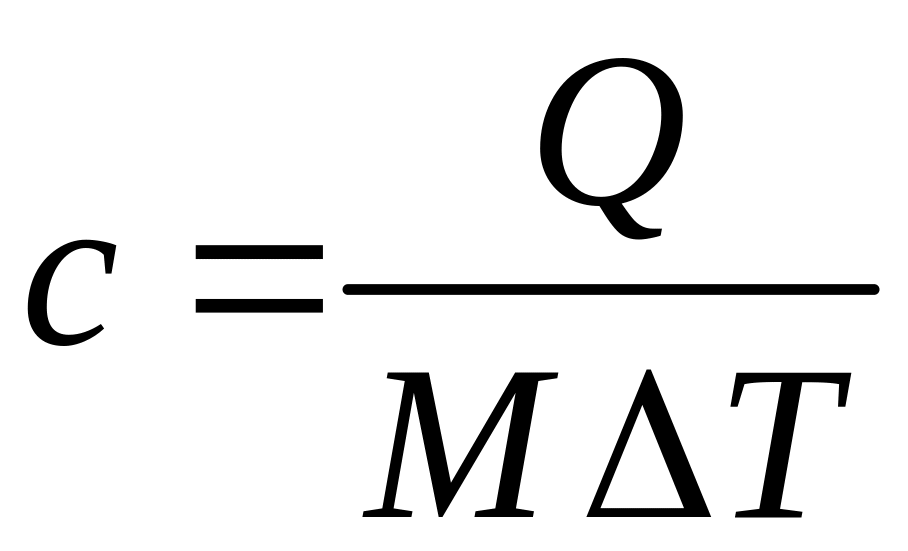, (3.1)

где М, кг – масса вещества;

– удельную объемную теплоемкость, Дж/(м³∙К):

, (3.2)

где V₀ , м³ – объем вещества при нормальных физических условиях (см. разд.1);

– удельную мольную теплоемкость, Дж/(кмоль∙К):

, (3.3)

где N, кмоль – количество киломолей вещества.

Различные виды удельных теплоемкостей связаны между собой простыми соотношениями:

, (3.4)

где , кг/м³ – плотность газа при н.ф.у;

μ, кг/кмоль – молекулярная масса газа.

В зависимости от характера термодинамического процесса подвода тепла различают теплоемкости при постоянном объеме с_v и при постоянном давлении с_p, связанные между собой формулой Майера

, (3.5)

где R, Дж/(кг ∙К) – газовая постоянная.

По классической (молекулярно-кинетической) теории теплоемкость газов не зависит от температуры, а определяется только количеством атомов в молекуле (числом степеней свободы молекулы f): . Определенные таким образом мольные теплоемкости газов приводятся в табл. 3.1, массовые и объемные теплоемкости рассчитываются по выражениям (3.4). Полученные значения хорошо совпадают с экспериментальными данными в области комнатных температур.

Отношение теплоемкостей

(3.6)

называется показателем адиабаты, который для идеального газа также зависит только от количества атомов в молекуле (табл. 3.1).

Таблица 3.1

Значения мольных теплоемкостей газов по классической теории

Вид газа	Число степеней свободы	Показатель адиабаты	Мольные теплоемкости, кДж/(кмоль∙К)
1-атомный	3	1,67	12,47	20,79
2-атомный	5	1,40	20,79	29,10
3-х и более атомный	6	1,33	24,94	33,26

Эксперимент показывает, что теплоемкости газов заметно изменяются с температурой. Истинной теплоемкостью газа при данной температуре является величина 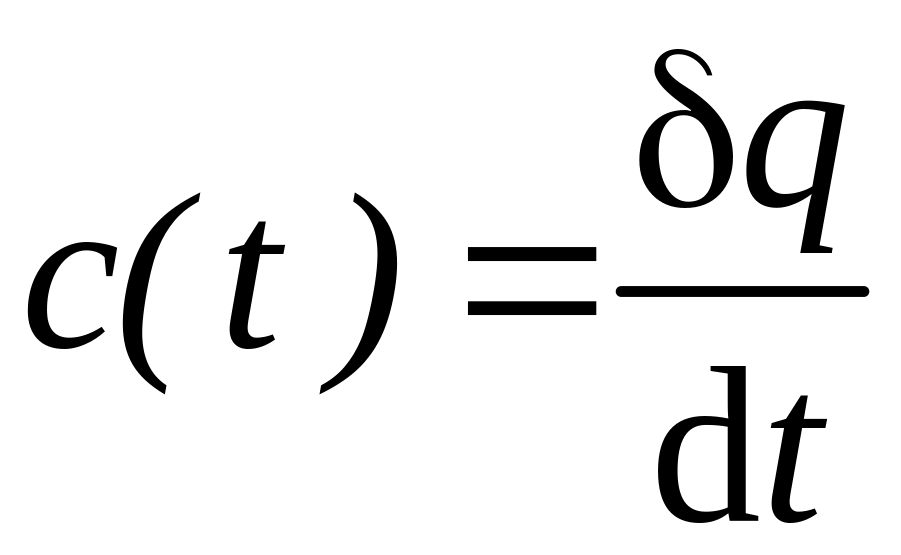. Тогда средняя теплоемкость газа в интервале температур ( ) находится по формуле

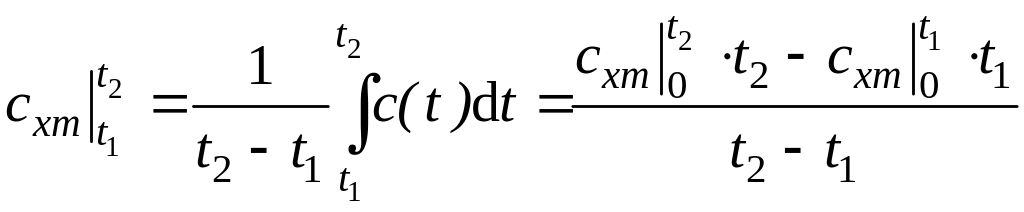, (3.7)

где – средние теплоемкости в интервалах температур , соответственно (берутся из таблиц – см. прил.1);

индекс x – обозначает характер процесса (p = const или v = const).

Средние массовая и объемная теплоемкости смеси газов находятся как

, (3.8)

где – соответственно массовые и объемные доли компонентов смеси.

Внутренняя энергия термодинамической системы U, Дж – это энергия, связанная с различными формами движения и взаимодействия ее структурных частиц (кинетическая энергия движения молекул, потенциальная энергия взаимодействия молекул и др.). Удельная внутренняя энергия – это энергия, отнесенная к единице массы системы , Дж/кг.

Внутренняя энергия является однозначной функцией состояния системы, т. е. зависит только от параметров термодинамической системы, например .

Для идеального газа внутренняя энергия зависит только от температуры и находится как:

. (3.9)

Энтальпия – это энергия расширенной термодинамической системы, включающей в себя саму систему и окружающую среду (оболочку, удерживающую систему в заданном объеме). Энтальпия H, Дж, и удельная энтальпия , Дж/кг, определяются как:

; (3.10)

. (3.11)

Энтальпия является однозначной функцией состояния системы, т. е. зависит только от параметров термодинамической системы, например .

Энтальпия идеального газа зависит только от температуры:

. (3.12)

В формулах (3.9), (3.12) теплоемкости газа при постоянном давлении с_р и при постоянном объеме с_v определяются либо методами молекулярно-кинетической теории по табл. 3.1, либо как средние теплоемкости в интервале температур от Т₁ до Т₂ по уравнению (3.7).

Задачи

3.1. Найти среднюю удельную теплоемкость c_p азота в интервале температур от 1000 ^оС до 2000 ^оС, если известно, что

Решение

Средняя теплоемкость в интервале температур от t₁ до t₂ вычисляется согласно формуле (3.7):

3.2. Найти объемную и массовую теплоемкости кислорода при постоянном объеме и постоянном давлении с использованием молекулярно-кинетической теории газов.

Решение

Согласно табл. 3.1 мольные теплоемкости двухатомных газов:

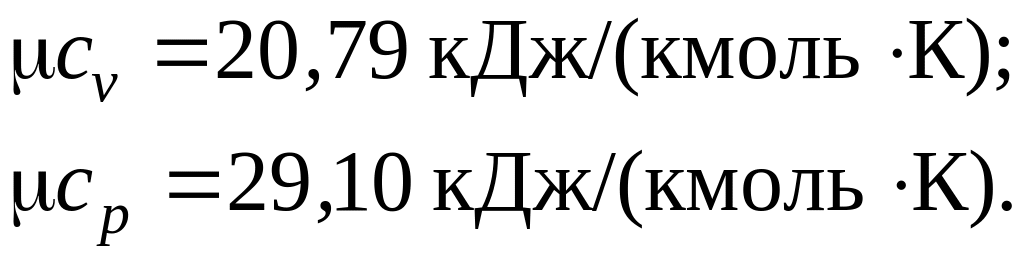
Тогда значения объемных и массовых теплоемкостей для кислорода с учетом (3.4):

3.3. Определить теплоту, необходимую для нагрева смеси газов массой 5 кг при постоянном давлении от температуры 40 ^оС до температуры 800 ^оС, если смесь газов имеет следующий массовый состав:_. 20 % – азот N₂; 80 % – углекислый газ CO₂. При расчетах:

а) учесть зависимость теплоемкости от температуры;

б) теплоемкости c_v и c_p вычислить методами молекулярно- кинетической теории.

Сравнить полученные результаты, определив относительную погрешность в вычислении теплоты.

Решение

Количество теплоты для смеси идеальных газов находится по формуле

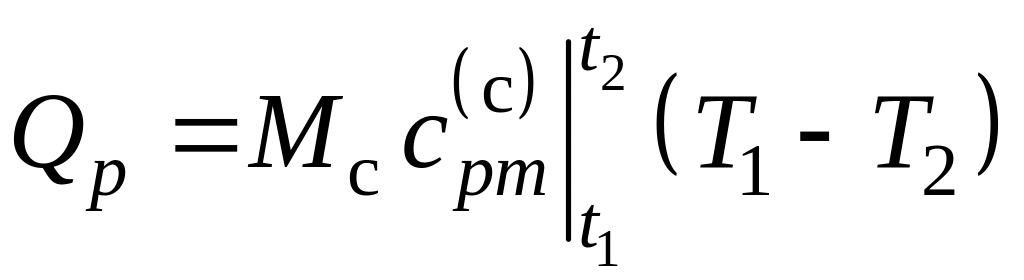, где .

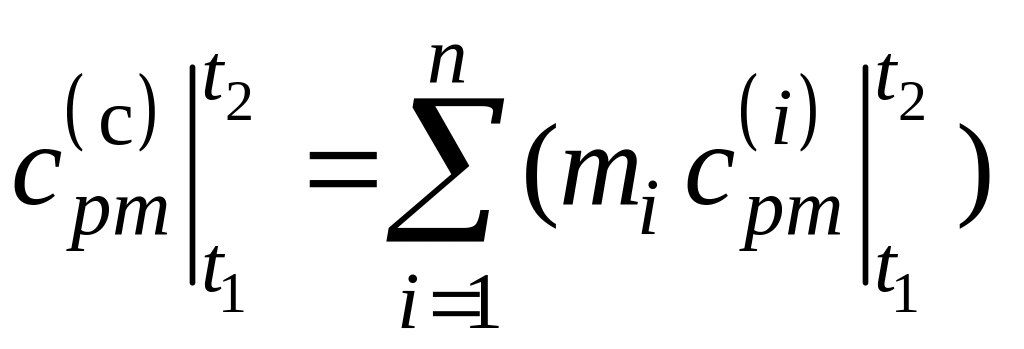а) Найдем среднюю удельную теплоемкость каждого компонента смеси в интервале температур (40–800 ^оС) по формуле 3.7. Для этого необходимо определить средние теплоемкости в интервалах температур (0–40 ^оС) и (0–800 ^оС), используя таблицу прил.1.

Поскольку в таблице значения удельных теплоемкостей даются с интервалом 100 ^оС, теплоемкости в интервале температур (0–40 ^оС) определяем путем интерполирования. Тогда:

;

;

;

;

;

.

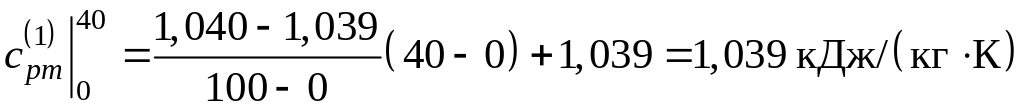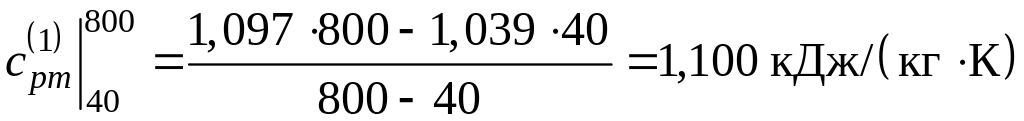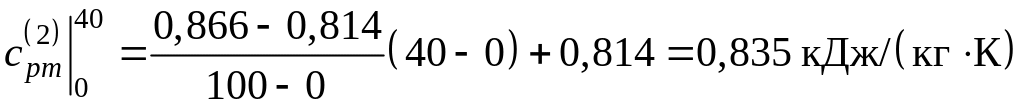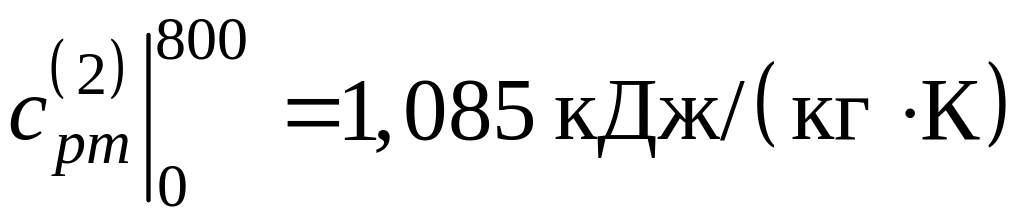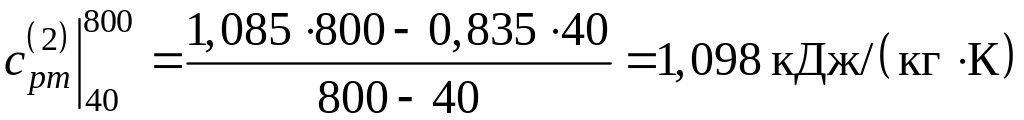Смесь газов задана массовым составом, следовательно, массовые доли компонентов: m₁ = 0,2 (азот); m₂ = 0,8 (углекислый газ).

Тогда средняя удельная теплоемкость смеси газов при постоянном давлении в заданном интервале температур будет равна

,

а количество теплоты, необходимой для нагрева смеси газов,

.

б) Для нахождения удельных массовых теплоемкостей компонентов смеси с помощью молекулярно-кинетической теории газов используем табл. 3.1. При этом учтем, что азот – двухатомный газ, а углекислый газ – трехатомный. Массовые теплоемкости:

;

.

Средняя теплоемкость смеси и количество необходимой для нагрева теплоты в этом случае будут равны

;

.

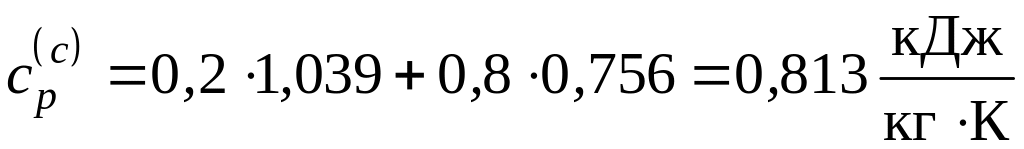Относительная погрешность в вычислении количества теплоты

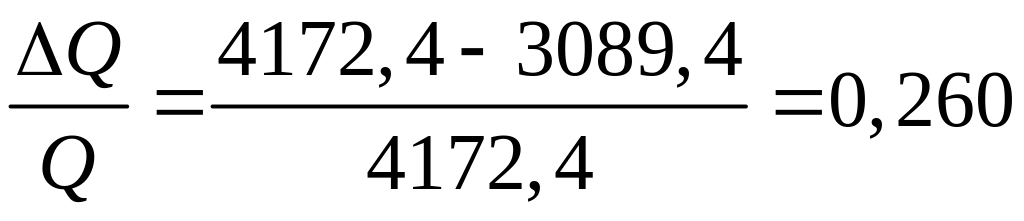или 26 %.

3.4. В объеме V₁ = 200 м³ при температуре t₁ = 100 ^оС и давлении p₁ = 3 бар находится смесь идеальных газов заданного объемного состава: 60 % – азот; 40 % – кислород.

Определить теплоту, необходимую для нагрева смеси газов при постоянном объеме до температуры 500 ^оС.

Ответ: 173,5 МДж.

3.5. Воздух с температурой 80 ^оС образуется в результате смешения при постоянном давлении двух потоков: холодного воздуха с температурой 0 ^оС и горячего воздуха с температурой 900 ^оС. Определить, сколько горячего и холодного воздуха необходимо взять для получения 1 кг смеси. При расчете теплоемкостей не учитывать их зависимость от температуры.

Ответ: 0,917 кг холодного воздуха и 0,083 кг горячего воздуха.

3.6. Определить средние массовые и объемные теплоемкости при постоянном давлении и постоянном объеме смеси газов в интервале температур от 0 до 1300 ^оС, если смесь имеет следующий объемный состав: 8 % – двуокись углерода СО₂; 2 % – окись углерода СО; 85 % – азот N₂; 5 % – водород Н₂.

Ответ:

3.7. Определить количество тепла, воспринятого воздухом в регенераторе газовой турбины от смеси газов заданного состава: СО – 2,1 %; СО₂ – 12,3 %; SO₂ – 1,8 %; N₂ – 83,8 % (по массе). Смесь газов охлаждается в регенераторе при постоянном давлении p = 1,2 бар от температуры 427 ^оС до 120 ^оС. Расход газов при начальных условиях 12500 м³/ч. КПД регенератора 0,95.

Ответ: Q = 2,36 ГДж/ч.

3.8. Определить удельный объем и массовую теплоемкость при постоянном объеме пара натрия при давлении p = 10 бар и температуре t = 927 ^оС, если известно, что при этих параметрах пар натрия является смесью одно- и двухатомных молекул следующего мольного состава: r_Na = 0,8628, = 0,1372. Найти парциальные давления одно- и двухатомных паров натрия. Теплоемкости газов, составляющих смесь, рассчитать согласно молекулярно-кинетической теории. Молекулярная масса натрия μ_Na = 23 кг/кмоль.

Ответ: v = 0,381 м³/кг; с_v = 520,44 Дж/(кгК);

p_Na = 8,628 бар; = 1,372 бар.

3.9. Определить мольную изобарную теплоемкость воздуха при температурах t₁ = 287 ^oC и t₂ = 560 ^oC, если известна интерполяционная формула для истинной мольной теплоемкости воздуха

и среднюю мольную изобарную теплоемкость воздуха в интервале температур (t₁ – t₂).

Результаты сравнить с табличными данными.

Решение

Подставив значения температур t₁ = 287 ^oC и t₂ = 560 ^oC в интерполяционную формулу, получим значения истинных мольных теплоемкостей при данных температурах:

Тогда средняя мольная изобарная теплоемкость воздуха в интервале температур ( t₁ – t₂) определится как

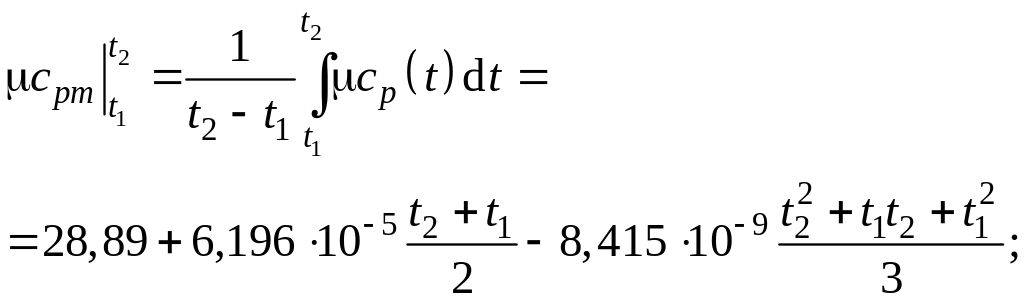
Рассчитанная с использованием таблиц прил.1 средняя теплоемкость воздуха в том же интервале температур, определяемая по формуле (3.7), оказывается равной

Расхождение результатов составляет 7,3 %.

3.10. Определить тепловую мощность , необходимую для нагрева при постоянном давлении p = 1,2 бар смеси газов состава:

от t₁ = 325 ^оС до t₂ = 800 ^оС. Расход смеси по параметрам на входе равен . Вычислить также массовый расход смеси.

Ответ:

3.11. Определить истинную изобарную массовую теплоемкость кислорода при температуре t = 1000 ^оС, если средняя теплоемкость в интервале температур (0–t ^оС) задается интерполяционной формулой

Решение

Из определения средней теплоемкости в каком-либо интервале температур (3.8) следует, что

или

Используя правила дифференцирования определенного интеграла по переменному верхнему пределу, получаем

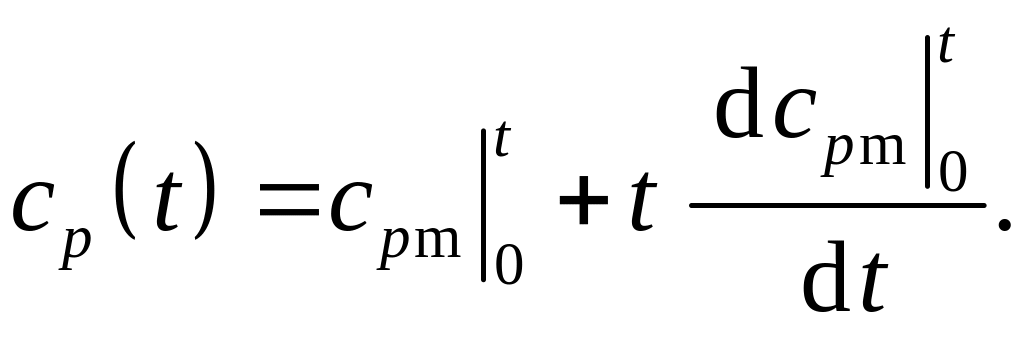
Вычисления дают:

3.12. Зависимость мольной изобарной теплоемкости газообразного фосфата кальция Ca₃(PO₄)₂ от температуры выражается уравнением

.

Найти значение мольной изобарной теплоемкости этого газа в интервале температур от 600 К до 900 К.

Решение

В соответствии с понятием определенного интеграла среднее значение теплоемкости в заданном интервале температур вычисляется как

Вычисления дают

3.13. В компрессоре газовой турбины сжимается воздух. Начальная температура воздуха t₁ = 30 ^oC, температура после сжатия t₂ = 150 ^oC. Определить изменение энтальпии и внутренней энергии воздуха в процессе сжатия, учитывая зависимость теплоемкости от температуры.

Ответ: