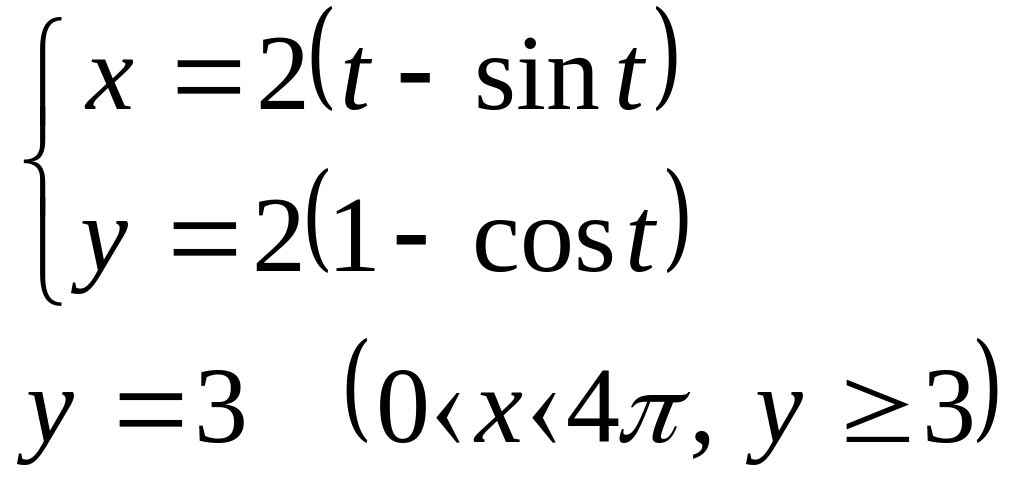10. Материалы для самостоятельной работы-1-сем
.doc
М ИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН
ИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН
Западно-Казахстанский аграрно-технический университет имени Жангир хана
Материалы
для самостоятельной работы по дисциплине
«Математика 1»
модуля М6 – высшая математика
(обязательный компонент)
(по выбору, обязательный)
для студентов 1 курса
машиностроительного факультета
специальности 5В070800-«Нефтегазовое дело»
форма обучения очная
на 1 семестр 2013-2014 учебного года
Уральск – 2014г.
Составители:
Махмудова Ш.Д.,
старшие преподаватели Уразгалиева А.Н., Умбеталиева Г.А.
Кафедра «Физика и математика»
Политехнический факультет, аудитория №201.
Количество кредитов – 3
Самостоятельная работа – 65 часов
Обсуждены на заседании кафедры «___»_______ 2013 г. Протокол №___.
Индивидуальное задание №1. (1-2 неделя)
Тема: «Система линейных уравнений и операции над матрицами»
Цель - усвоить понятие определителя, правила вычисления обратной матрицы.
Задание: |
Балл |
|
Задача №1. Решить систему уравнений с 3-мя неизвестными. Задача №2. Решить систему уравнений с 4-мя неизвестными. |
методом Крамера |
50 |
методом Гаусса |
50 |
|
Задача №3. Операции над матрицами. |
А) Транспонировать матрицу. В) Найти ранг матрицы. С) Найти обратную матрицу. Д) Решить СЛУ с тремя неизвестными матричным методом |
100 |
Итого: |
200 |
|
Вариант№9.
Задача №1. ![]() Задача
№2.
Задача
№2. ![]()
Задача №3. А)
![]() ; В)
; С)
; В)
; С)
![]()
Индивидуальное задание№2.
Тема: «Векторное исчисление» (3 неделя)
Цель – усвоить приложения векторного исчисления и методы решения задач аналитической геометрии.
Дано координаты точек А, В, С, А![]()
Записать векторы
 в системе
в системе
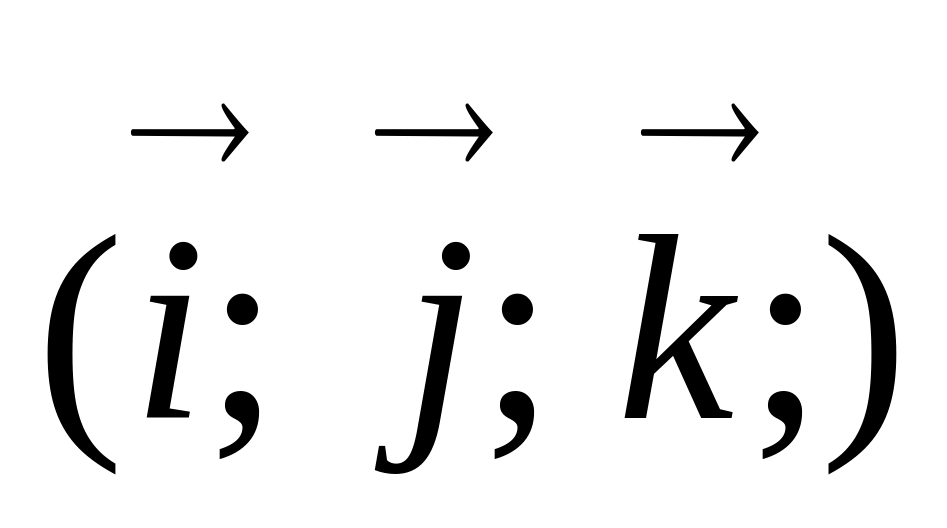 ,
найти модули этих векторов.
,
найти модули этих векторов.Найти координату т.Д (х, у, z) так, чтобы АВСD –стало основанием параллелепипеду
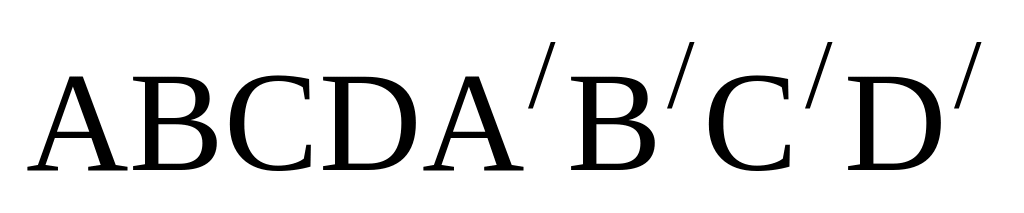 .
Найти cos
.
Найти cos
 ;
;
 .
.Проверить образует ли базис вектора
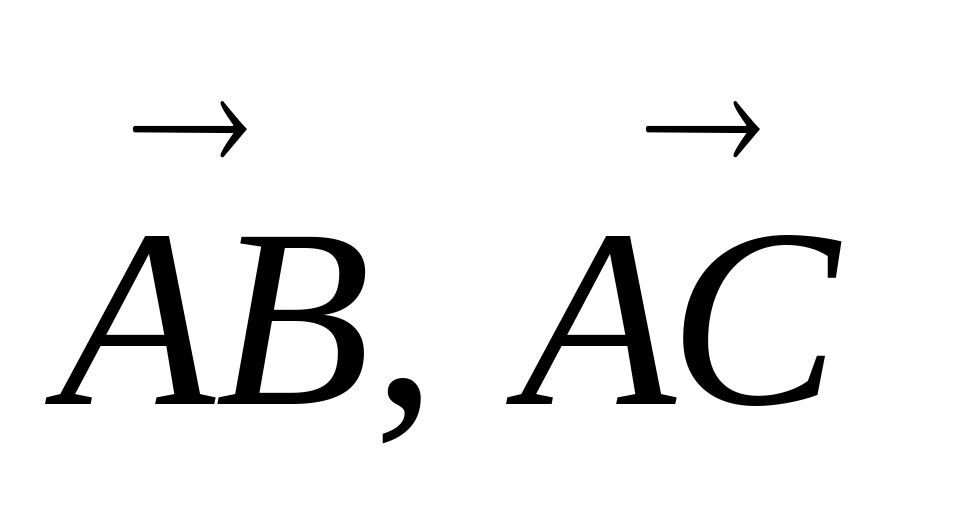 на плоскости и вектора
в пространстве.
на плоскости и вектора
в пространстве.Найти площадь параллелограмма
 и объем параллелепипеда построенного
на векторах
.
и объем параллелепипеда построенного
на векторах
.
№ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2, -2, 0) |
(0, -2, 2) |
(-2, 0,0) |
(0, 0, 4) |
Индивидуальное задание №3
Тема «Аналитическая геометрия». (5 неделя)
Вариант №9
Найти уравнение плоскости, проходящей через точку
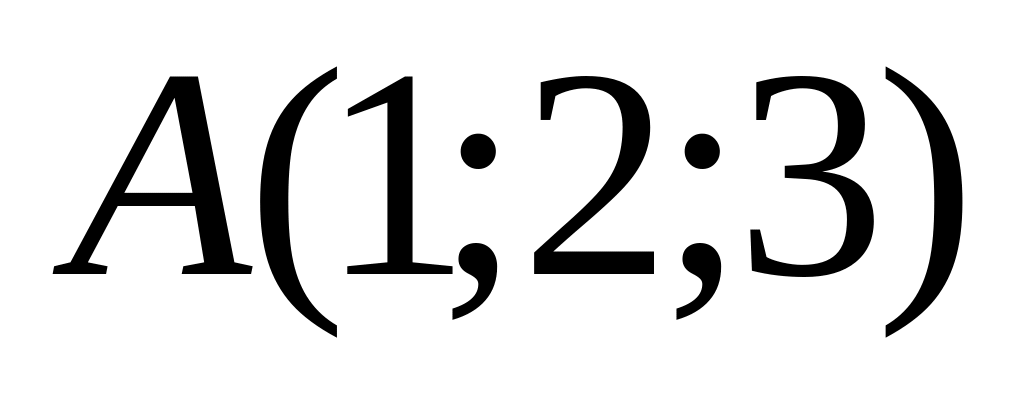 перпендикулярно вектору
перпендикулярно вектору
 .
.Найти угол между прямыми
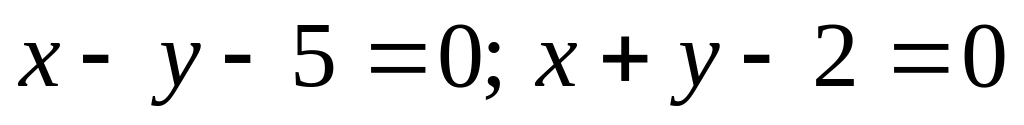 .
.При каком значении
 прямые
прямые
 и
и
 параллельны?
параллельны?Найти угол между плоскостями
 .
.Найти параметрическое уравнение прямой, проходящей через точки
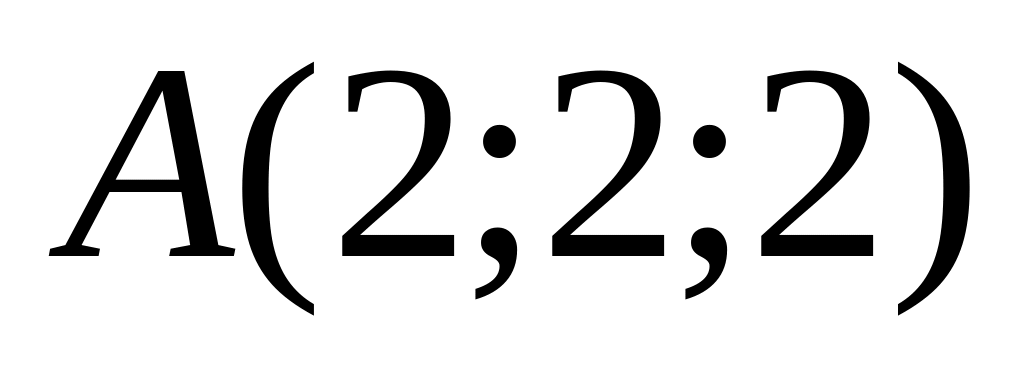 и
и

Написать уравнение плоскости проходящей через точку М(1,-2,3) перпендикулярно к данной прямой
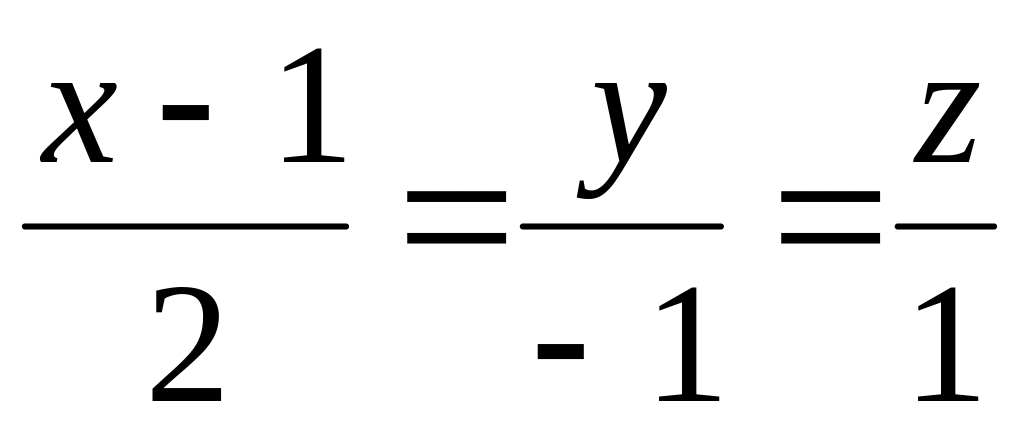 .
.Найти угол между прямыми
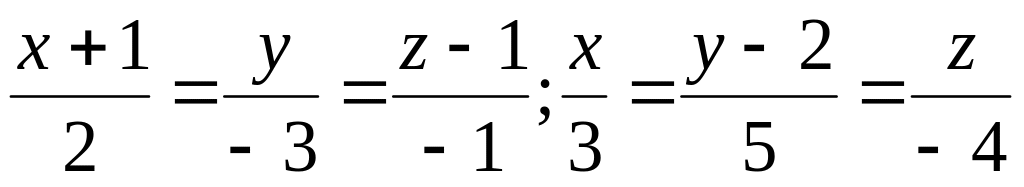
Уравнение прямой привести к каноническому виду
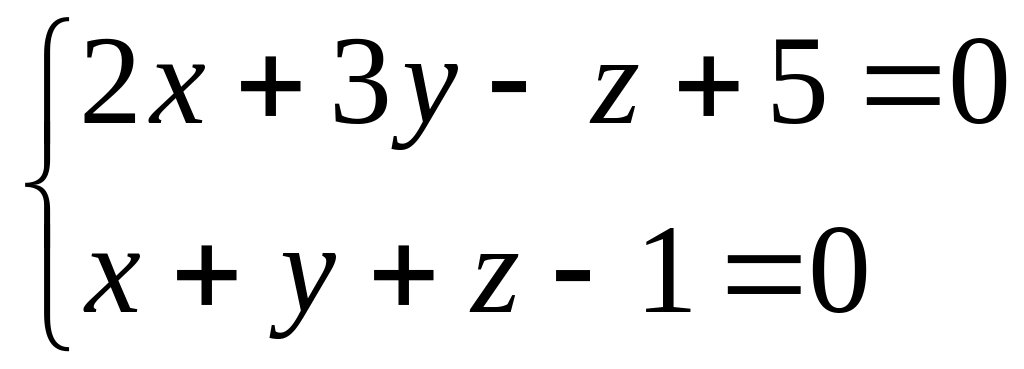 .
.Написать уравнение плоскости проходящей через три данные точки
![]()
Найти проекцию точки В(2,-2,-2) на плоскость

Индивидуальное задание№4. (8 неделя)
Темы: «Пределы»
Вариант №9, 19.

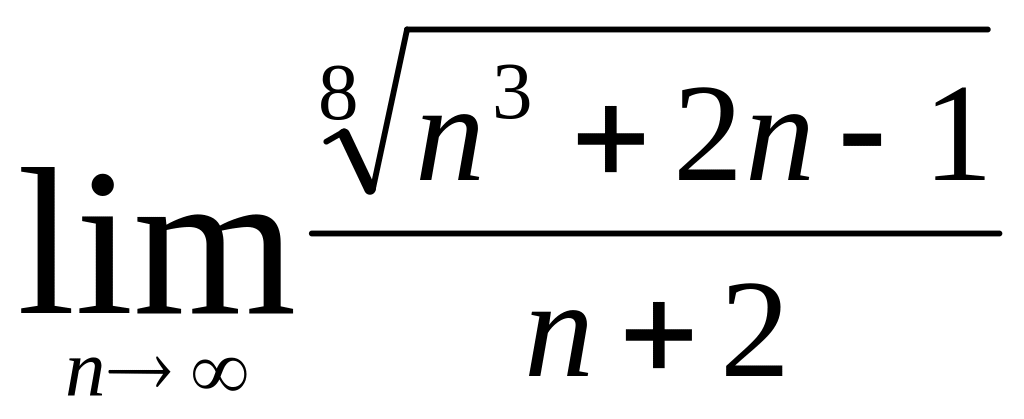

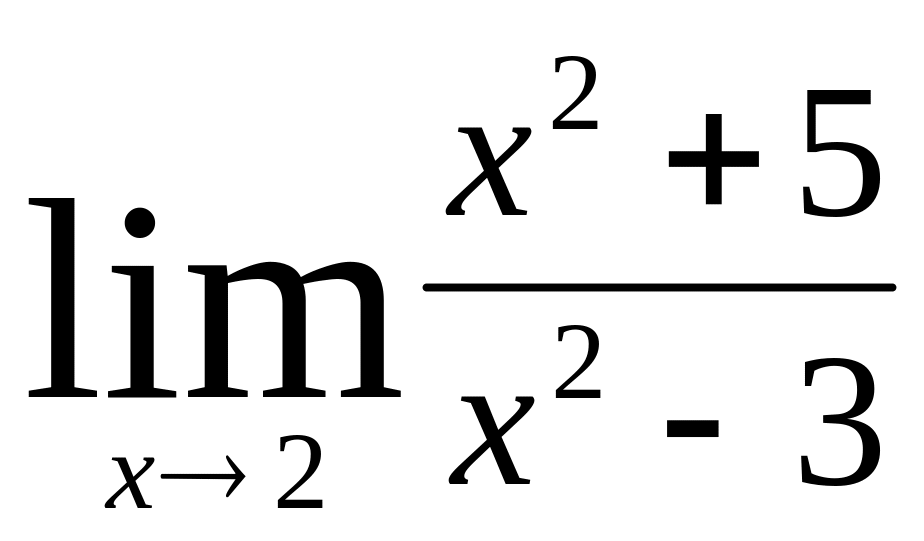
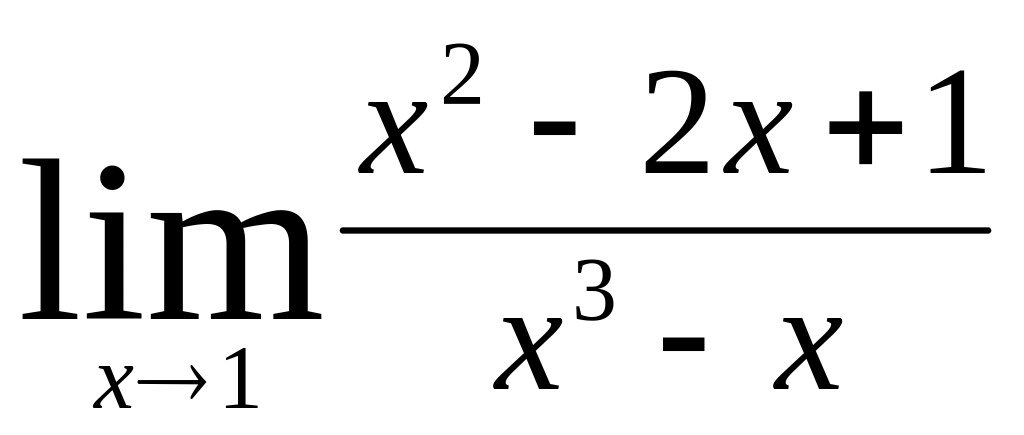

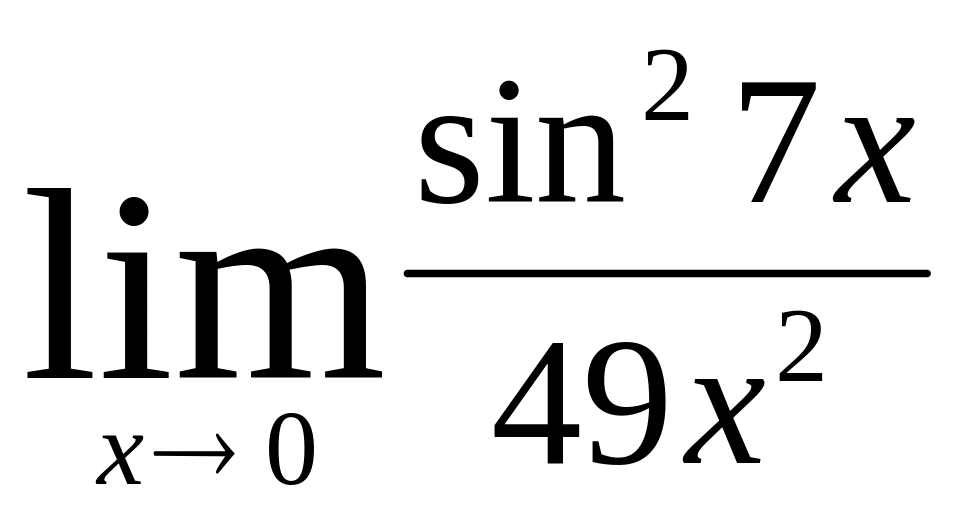

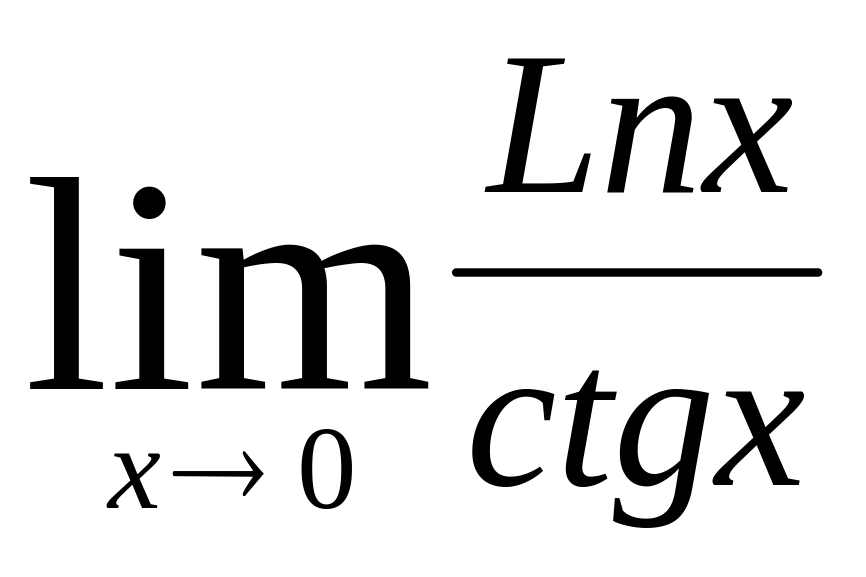

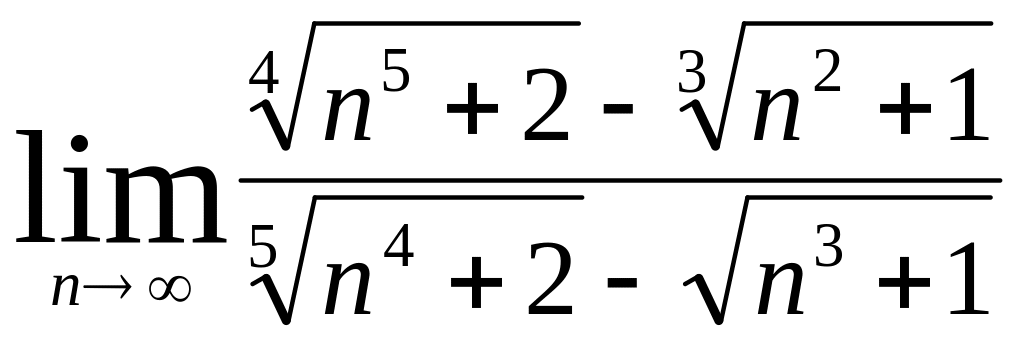


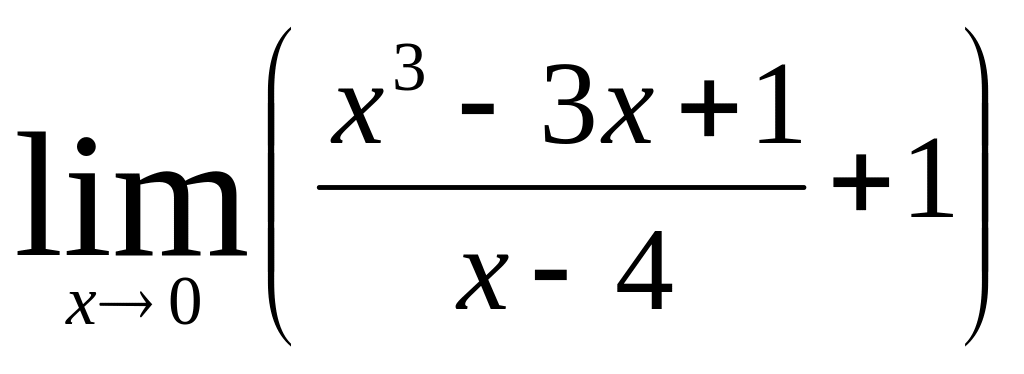

 (m и n
- целые числа)
(m и n
- целые числа)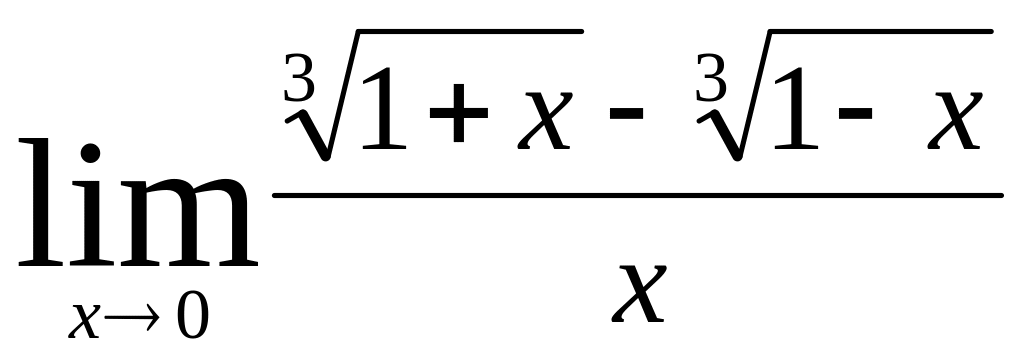
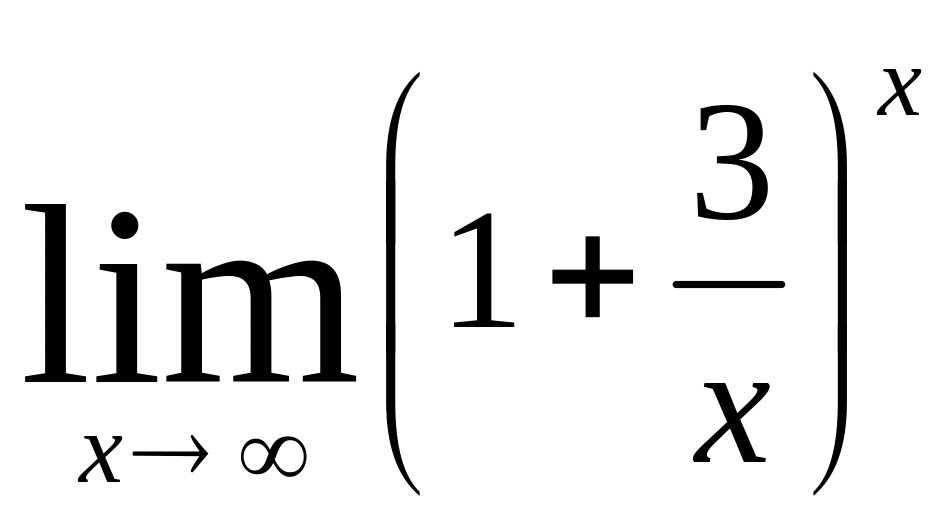
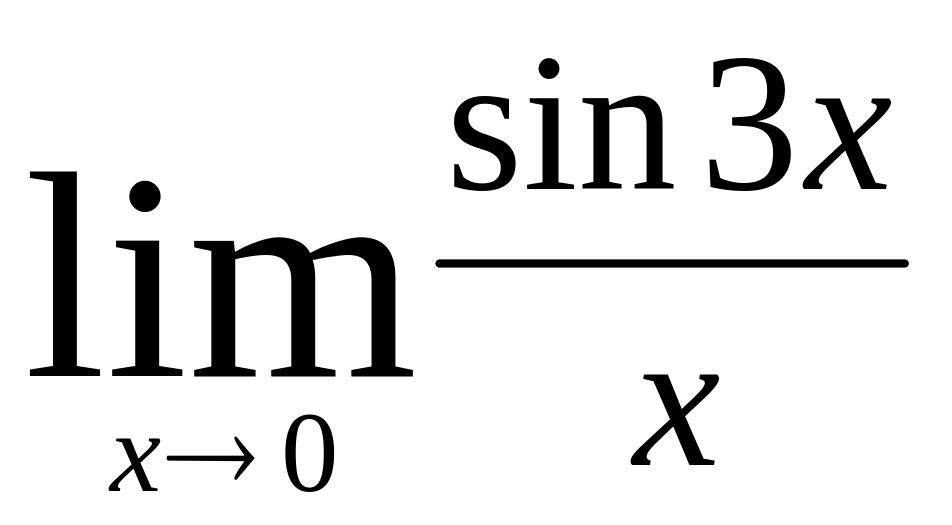

Индивидуальное задание № 5 (9 неделя)
Тема: «Производная функции»
Вариант 9-19


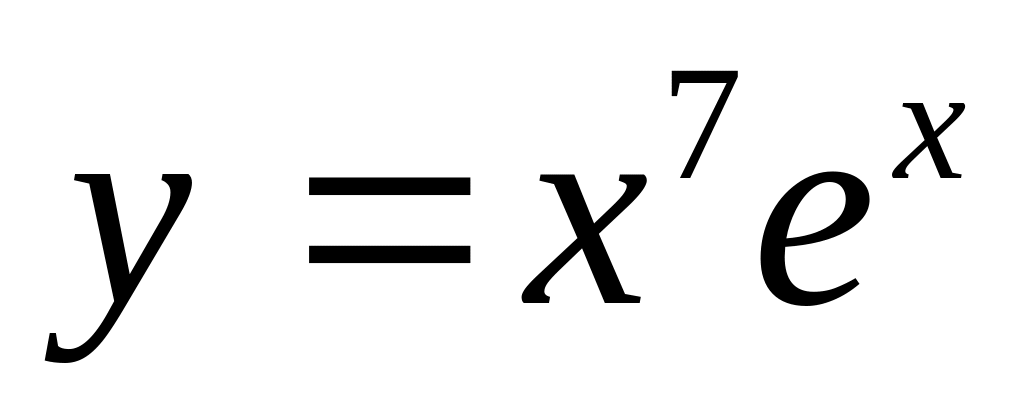
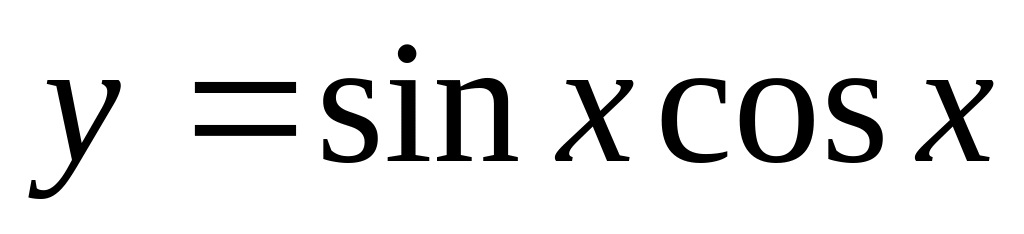






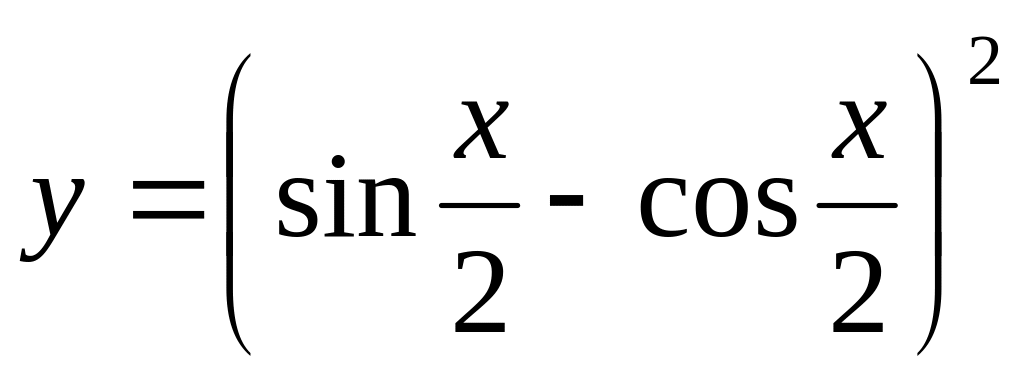
Вычислить
 :
: 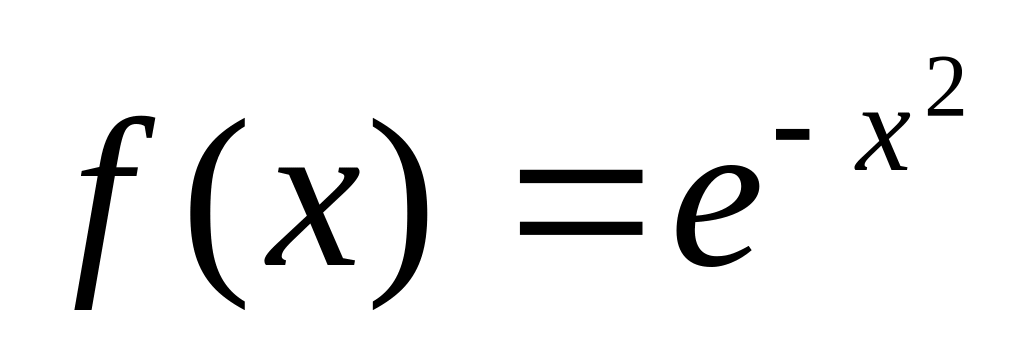
Вычислить
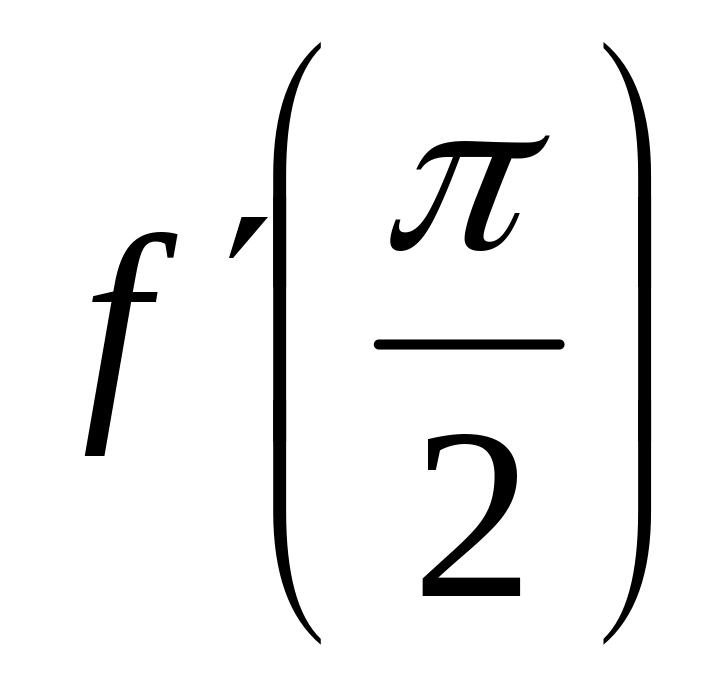 :
: 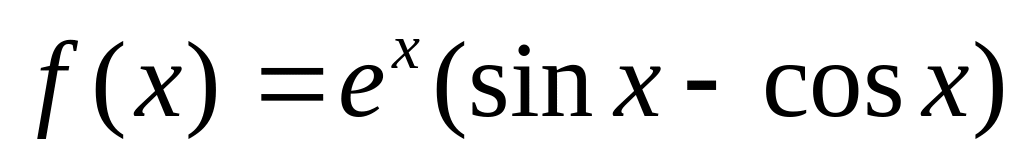
В какой точке касательная к параболе
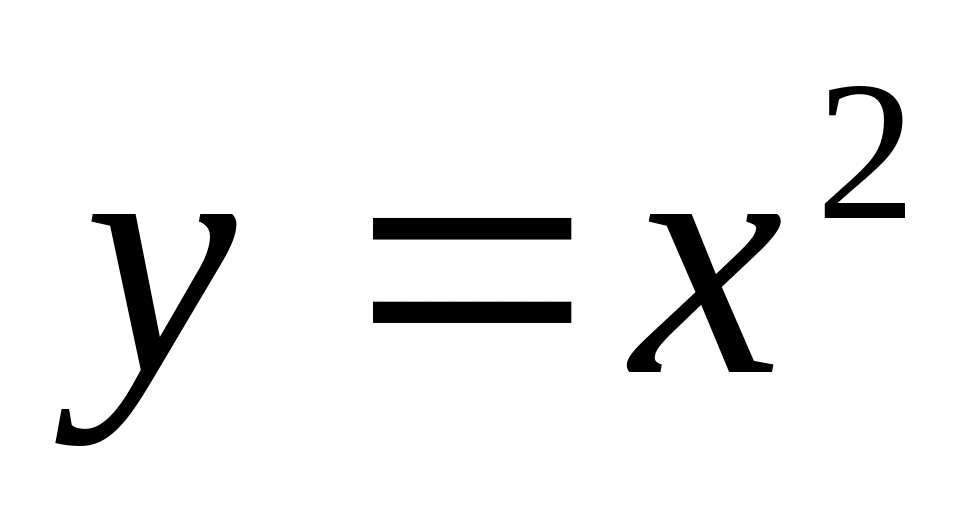 образует с осью Ох угол
образует с осью Ох угол
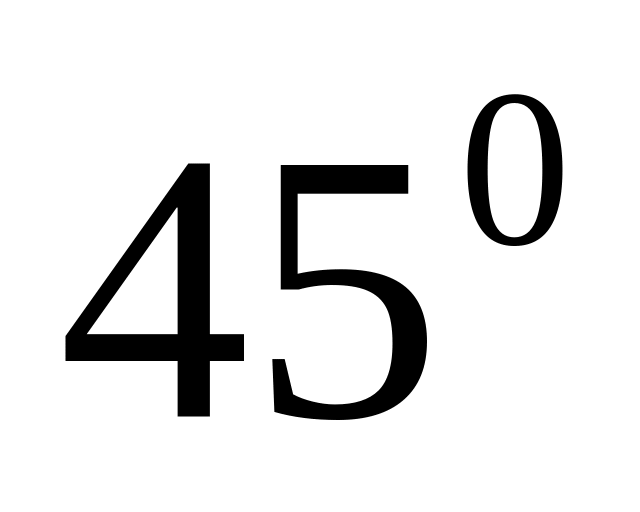 ?
?Найти угловой коэффициент касательной к кривой
 в точке
в точке
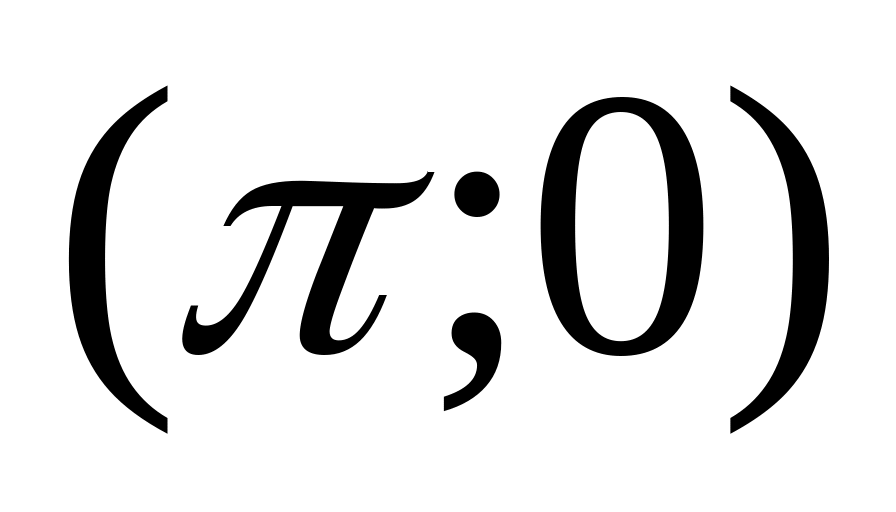 .
.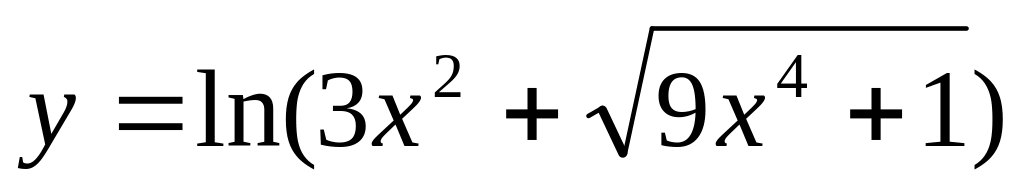
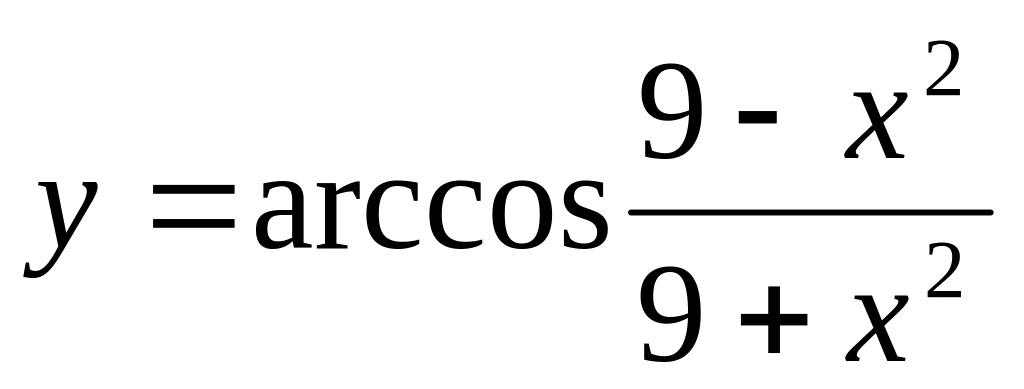
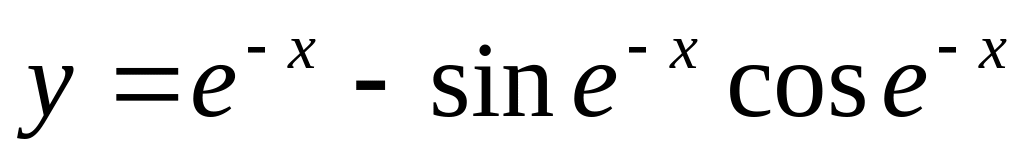

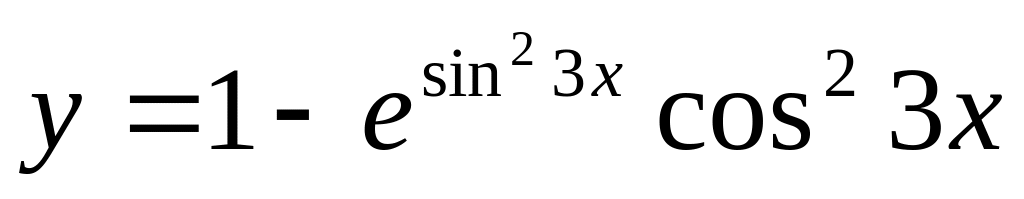

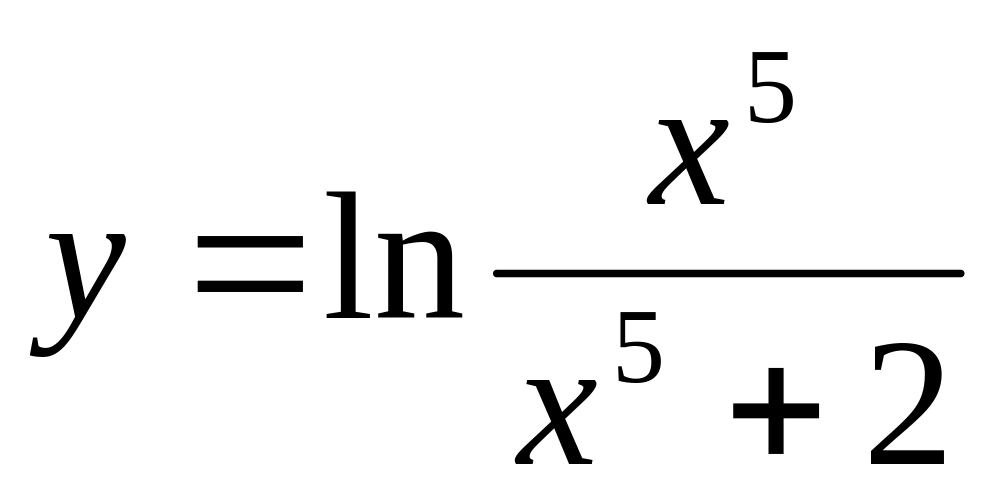 ; (Логарифмическое
дифференцирование)
; (Логарифмическое
дифференцирование)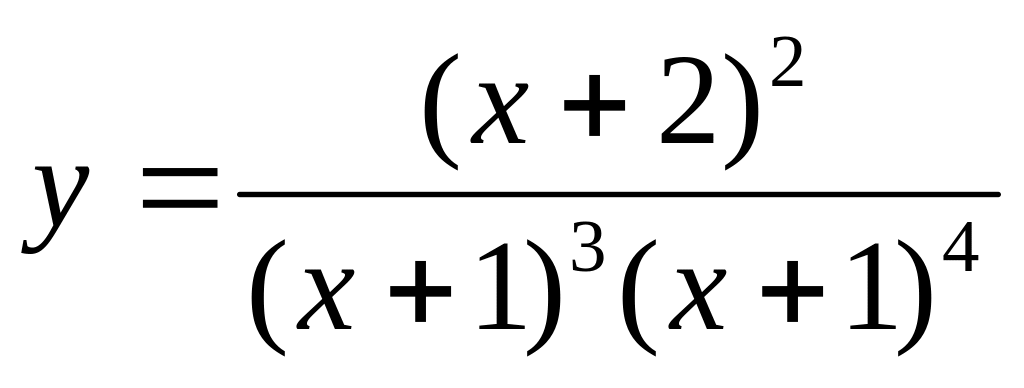 ;
(Логарифмическое дифференцирование)
;
(Логарифмическое дифференцирование)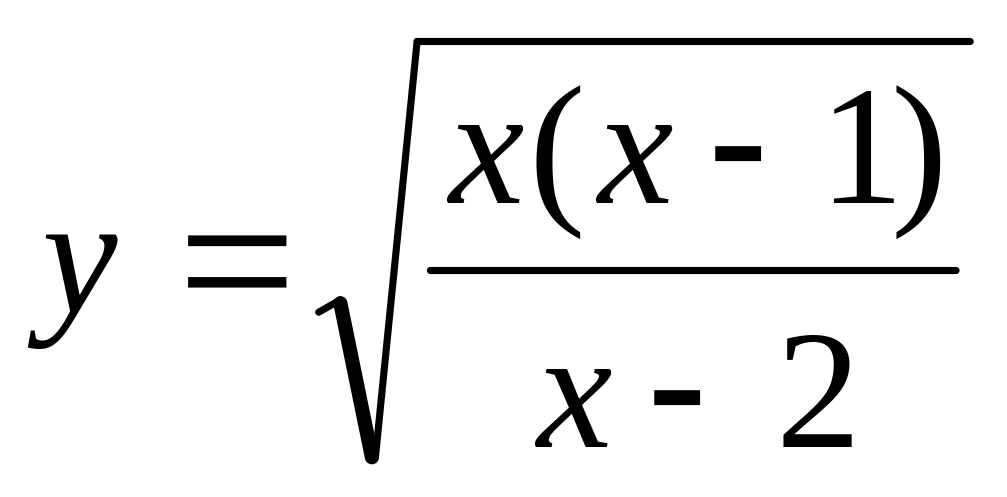 ;
(Логарифмическое дифференцирование)
;
(Логарифмическое дифференцирование)Найти производную
 от неявной функции
от неявной функции
 .
.
![]()
Индивидуальное задание № 6. (10 неделя)
Тема: «Исследование функции»
1. Найти область определения функции и исследовать поведение функции в граничных точках.
2. Выяснить симметричность графика и периодичность.
3. Найти точки разрыва функции и промежутки непрерывности.
4. Найти критические точки функции.
5. Определить точки перегиба, точки экстремумов, интервалы выпуклости, вогнутости, возрастания, убывания.
6. Найти асимптоты в случае их существования.
7. Построить график функции.
№ |
Задание |
№ |
Задание |
1 |
|
11 |
|
2 |
|
12 |
|
3 |
|
13 |
|
4 |
|
14 |
|
5 |
|
15 |
|
6 |
|
16 |
|
7 |
|
17 |
|
8 |
|
18 |
|
9 |
|
19 |
|
10 |
|
20 |
|
Индивидуальное задание №7 (12- 13 неделя)
Тема: «Неопределенный интеграл»
№ |
Задание |
Срок сдачи |
Балл |
1 |
Вычислить интегралы применяя методы интегрирования 1-20 |
12 неделя |
100 |
2 |
Вычислить интегралы от иррациональных функции 20-40 |
13 неделя |
100 |
Вариант №9, 19.
 ;
; ;
;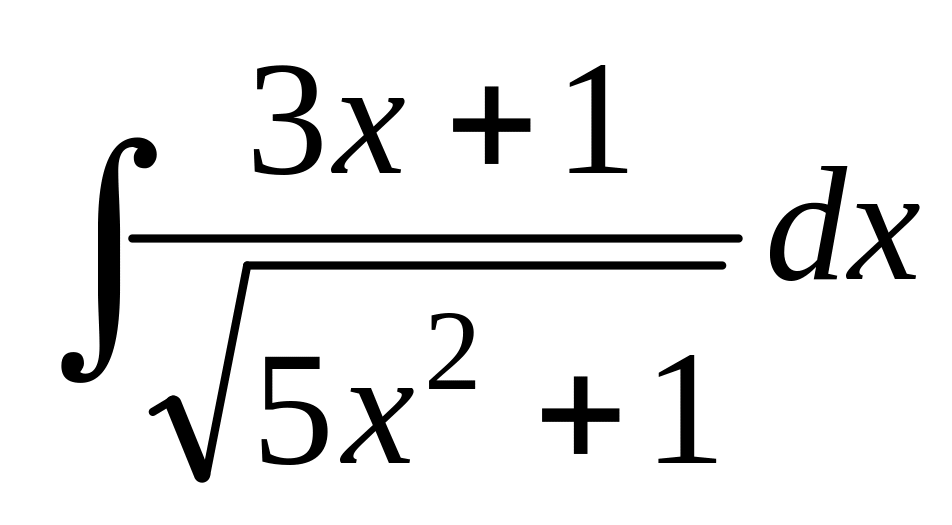 ;
;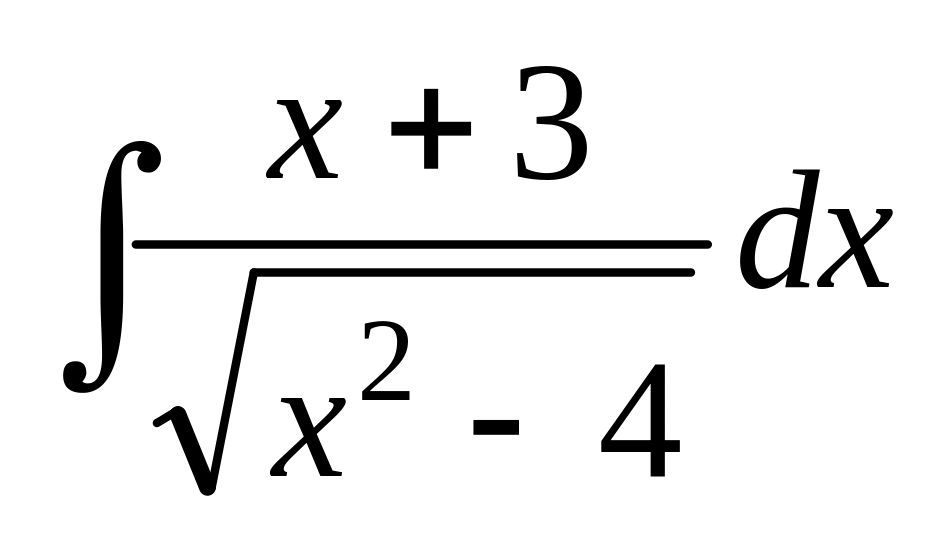 ;
;
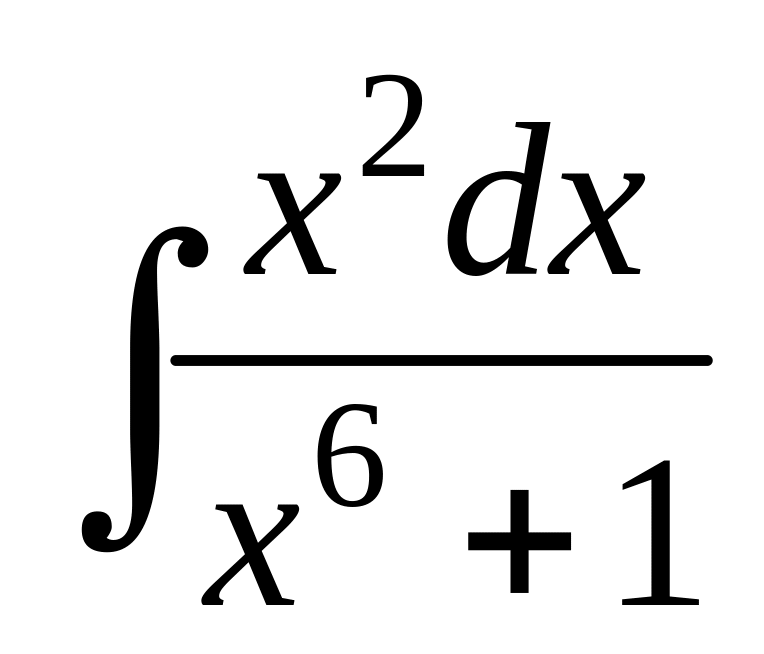 ;
; ;
; ;
; ;
;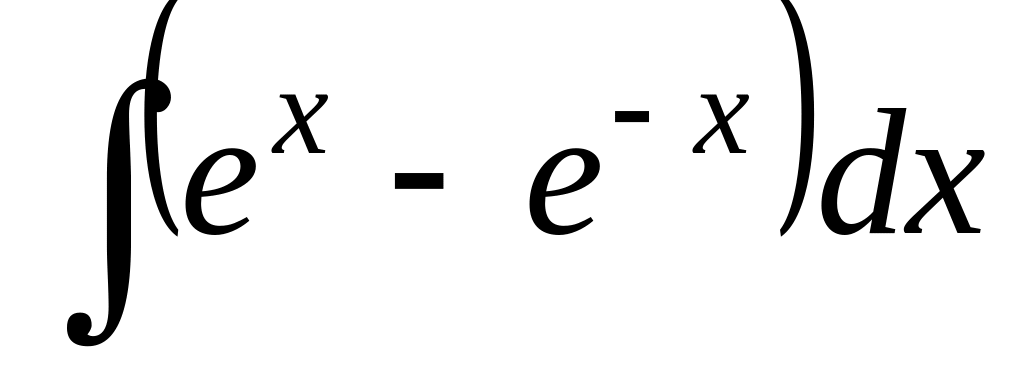 ;
;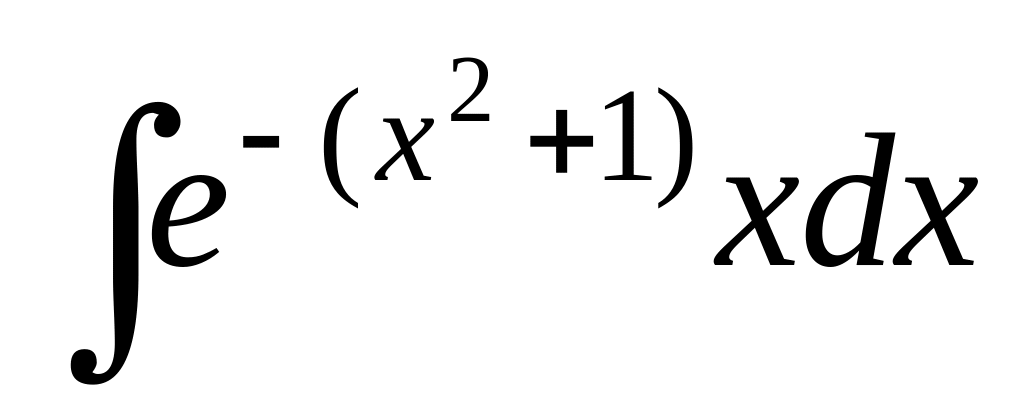 ;
; ;
; ;
; ;
; ;
;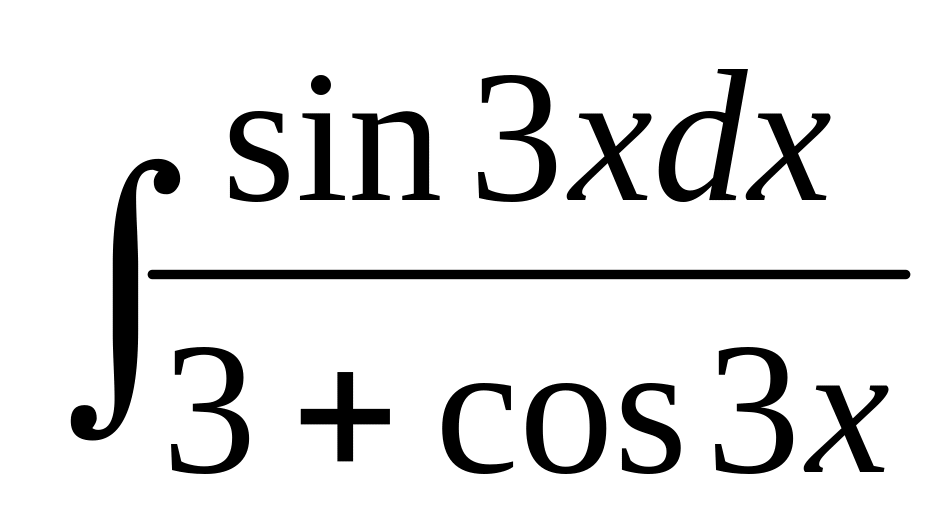 ;
; ;
; ;
;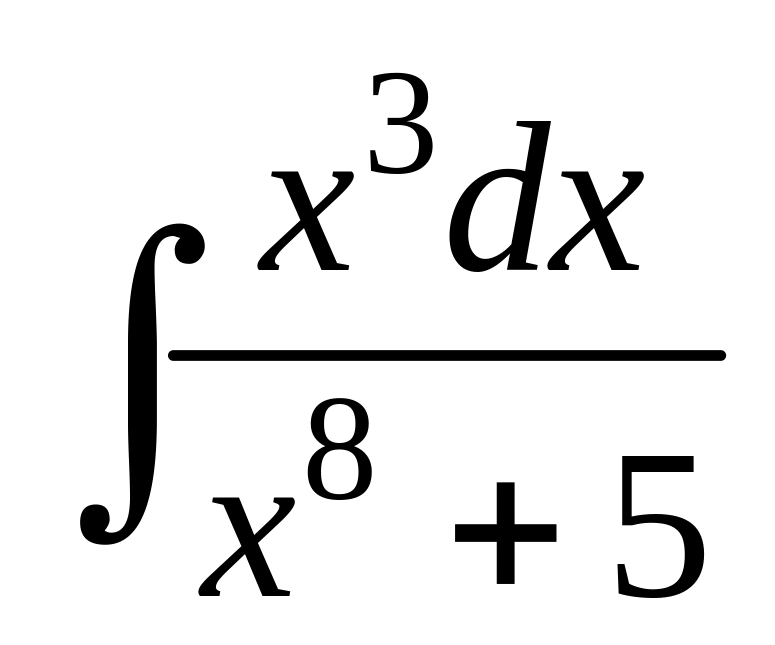 ;
; ;
; ;
; ;
; ;
;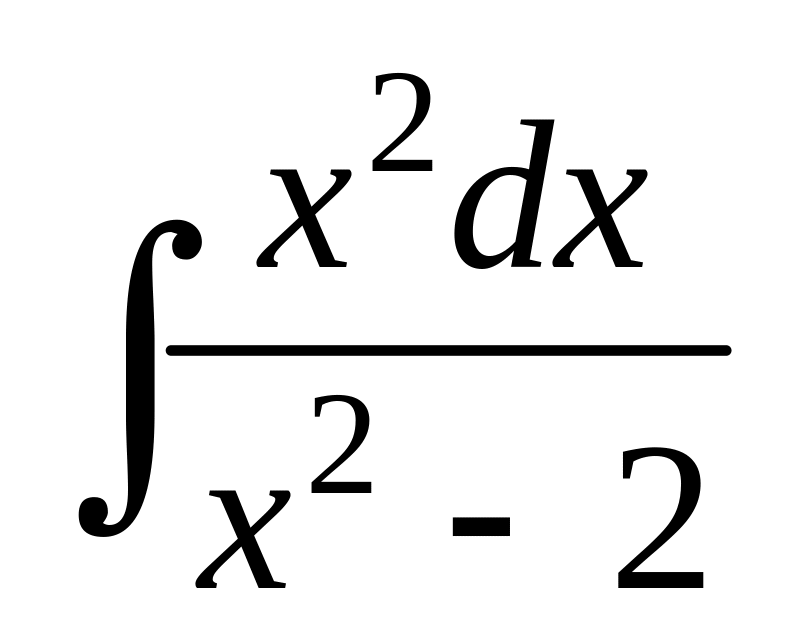 ;
; ;
;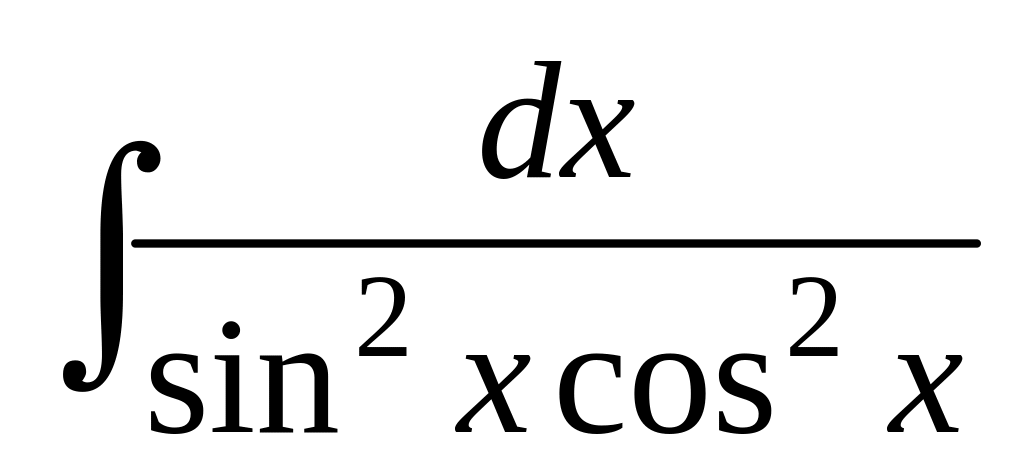 ;
; ;
;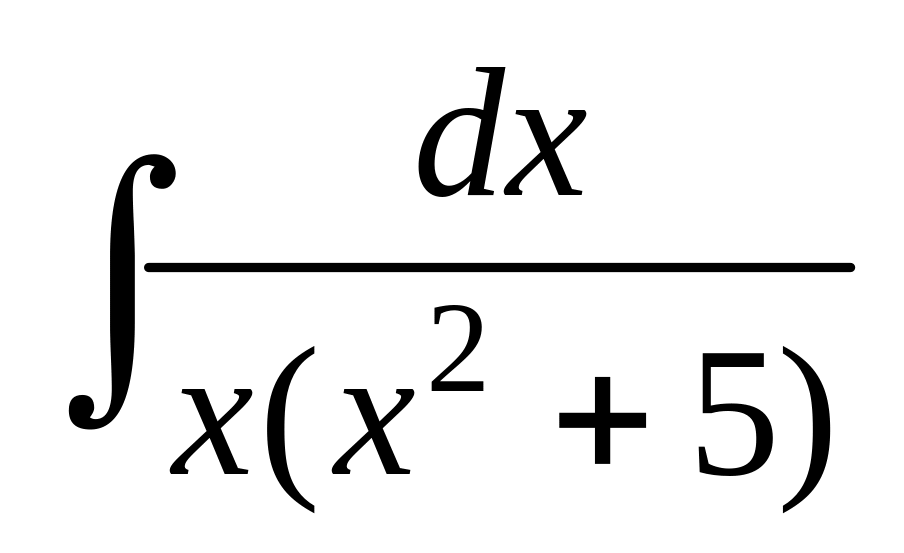 ;
;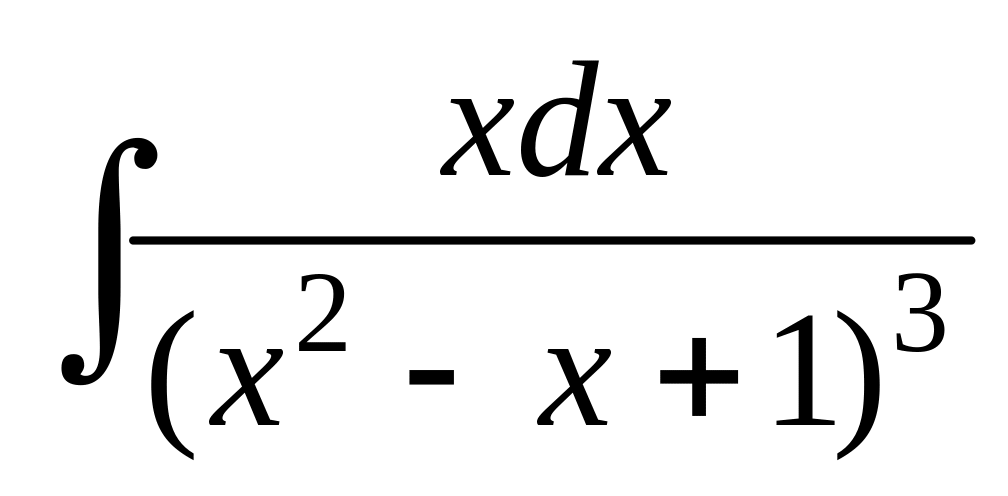 ;
;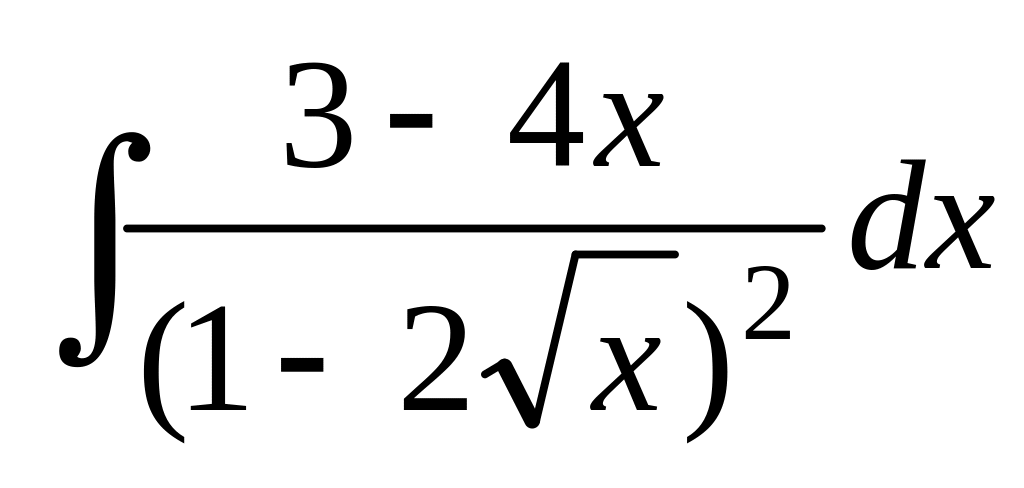 ;
;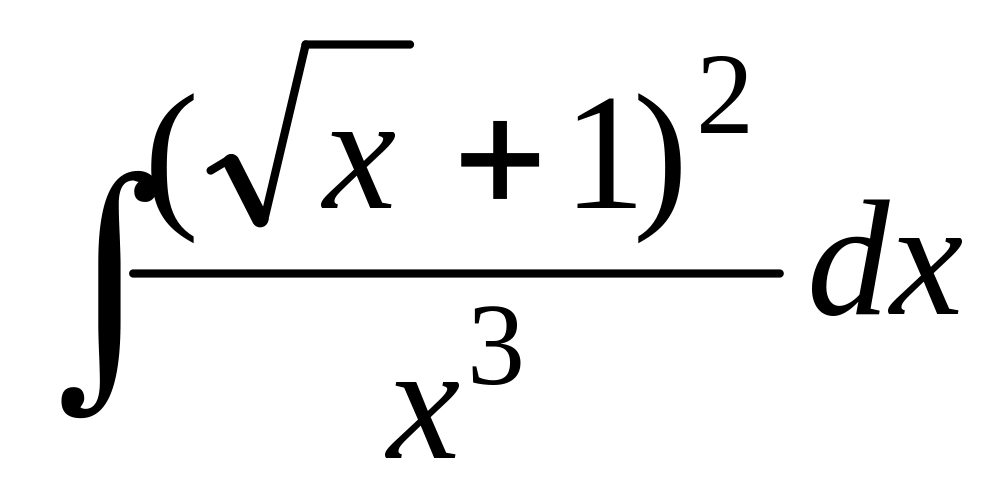 ;
;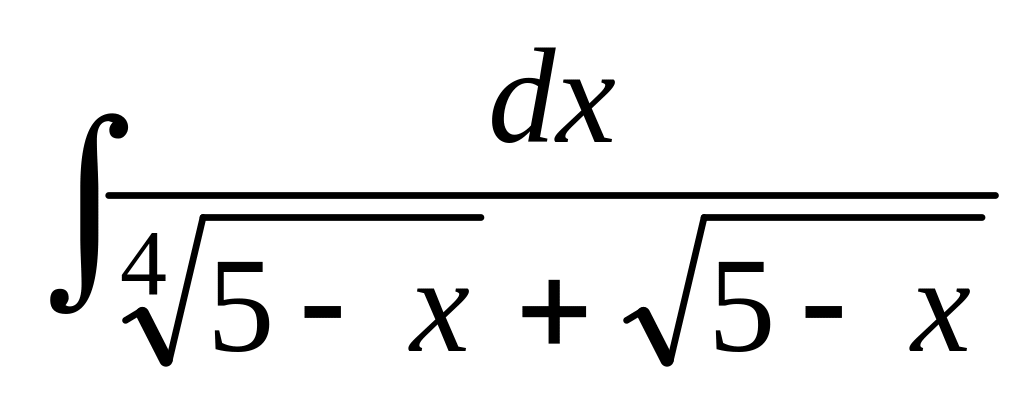 ;
;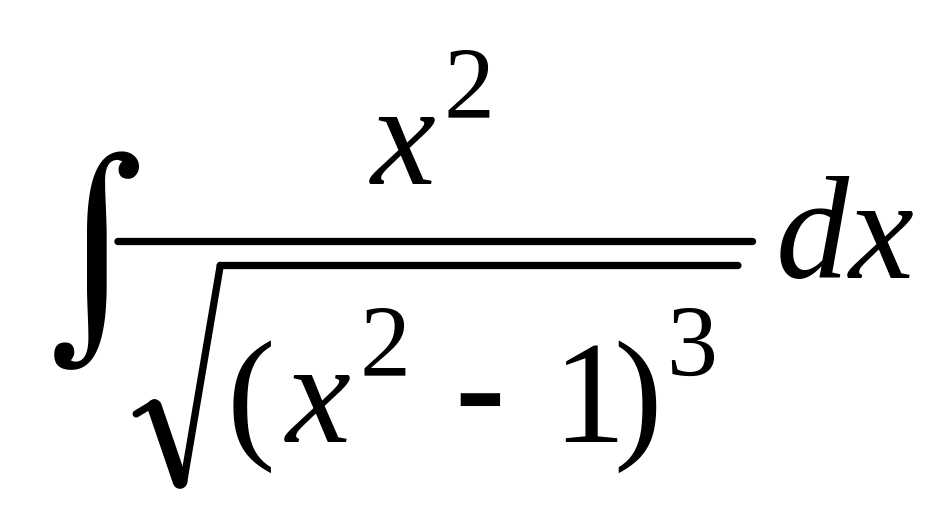 ;
; ;
; ;
; ;
;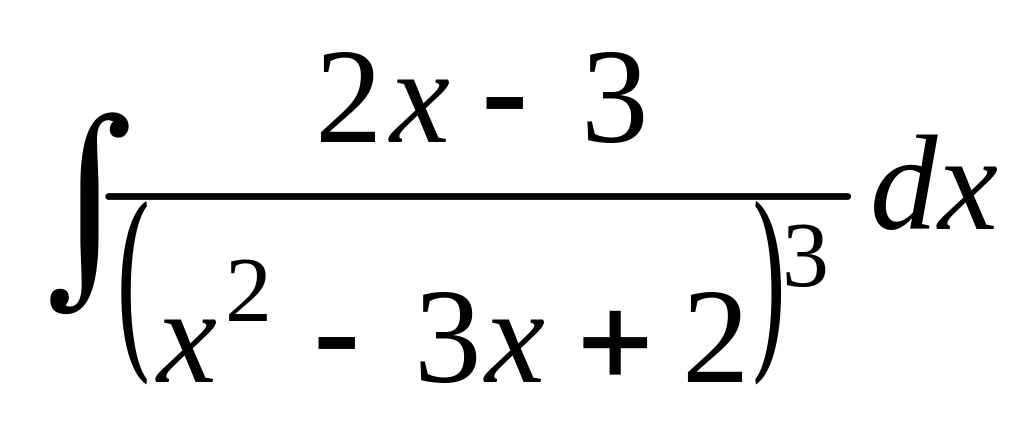 ;
; ;
;
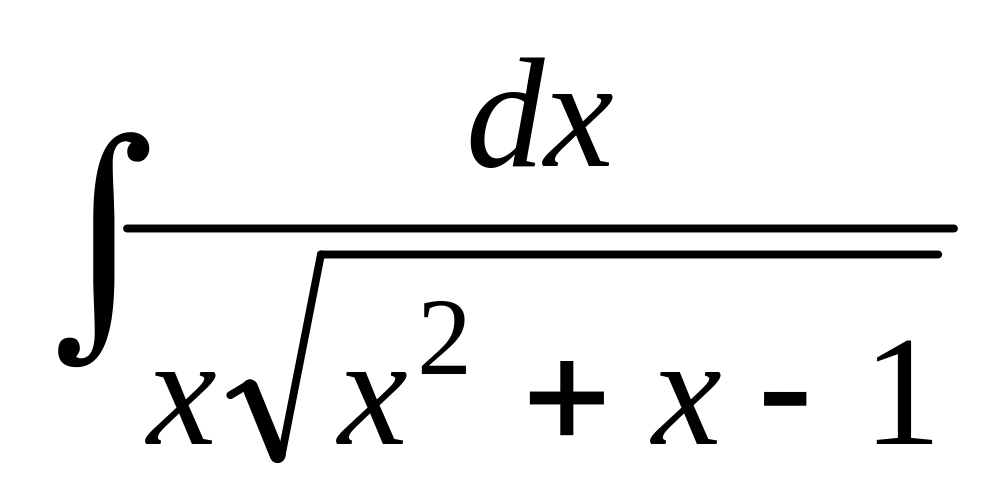
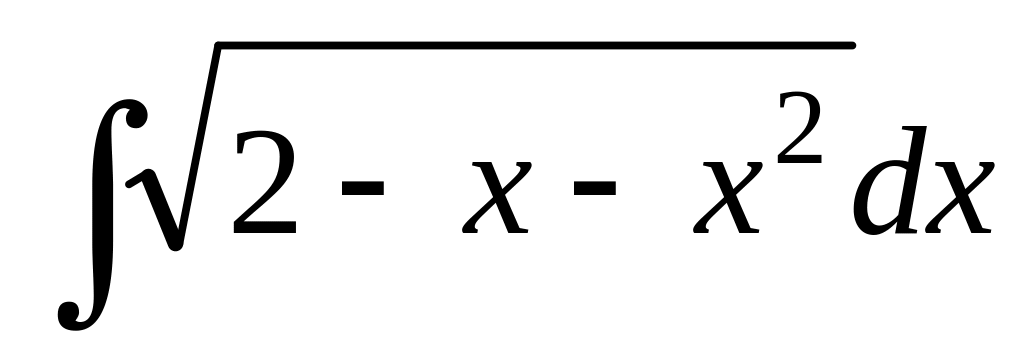
Индивидуальное задание№8. (15 неделя)
Тема: «Определенный интеграл и его приложения»
Цель - получение навыков вычисления и применения интегралов.
Задание:
Задание: |
Баллы |
Задача №1. Площадь плоской фигуры. |
20 |
Задача №2. Длина дуги кривой. |
30 |
Задача №3. Объем тела вращения. |
50 |
Всего: |
100 |
Площади плоских фигур.
Вычислить площадь фигуры, ограниченных графиками функций.
 Ответ:
8
Ответ:
8

Ответ:
![]()
Ответ: 9
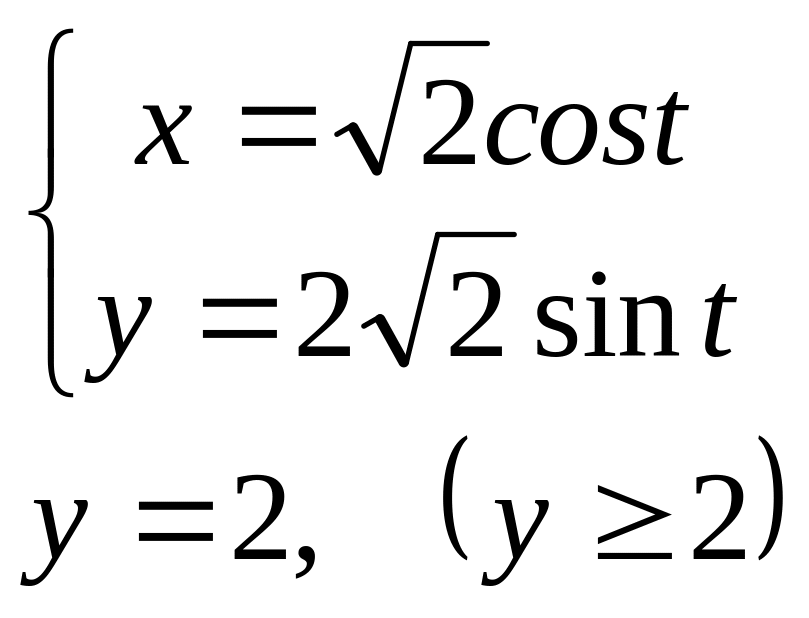 Ответ:
Ответ: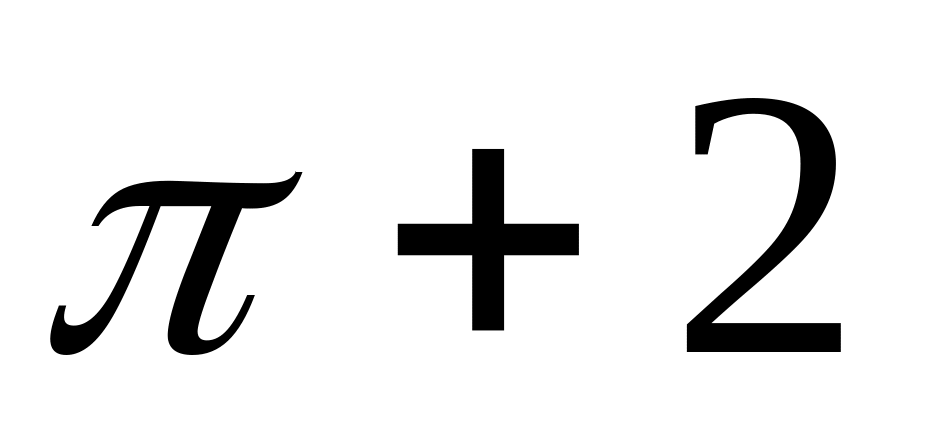
 Ответ:
Ответ:
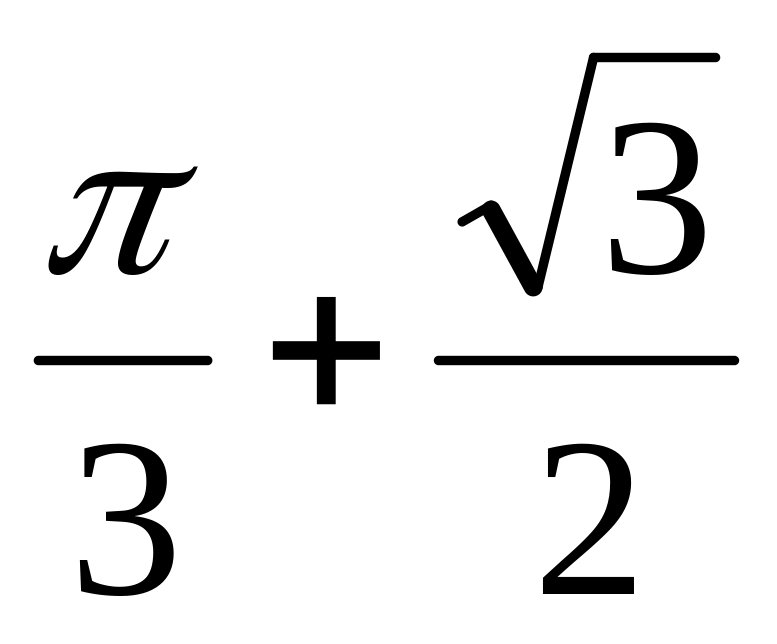
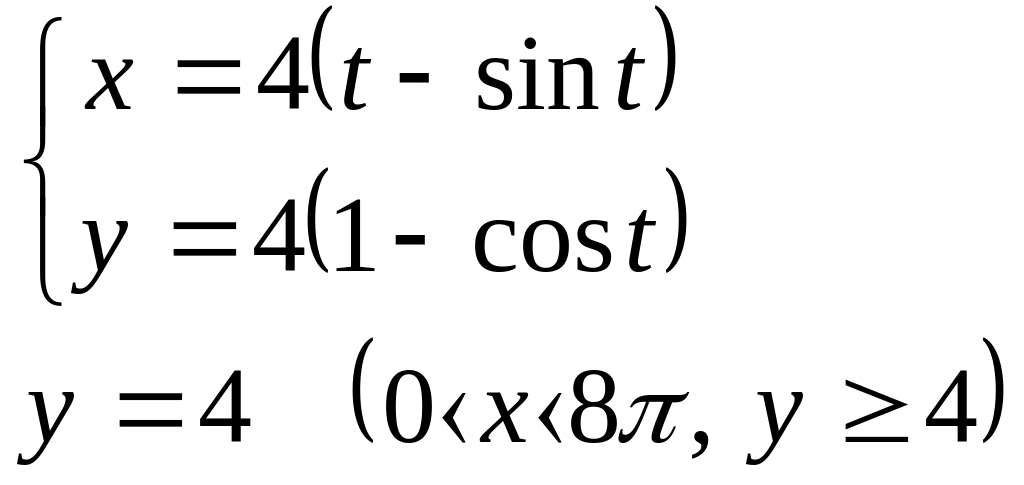
Ответ:![]()
 Ответ:
Ответ:

 Ответ:
Ответ:
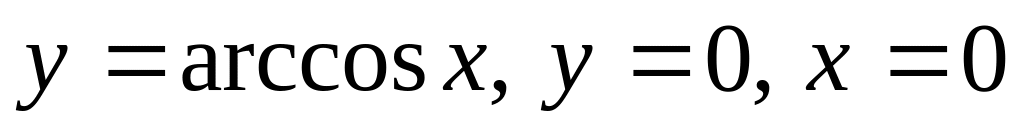
Ответ: 1
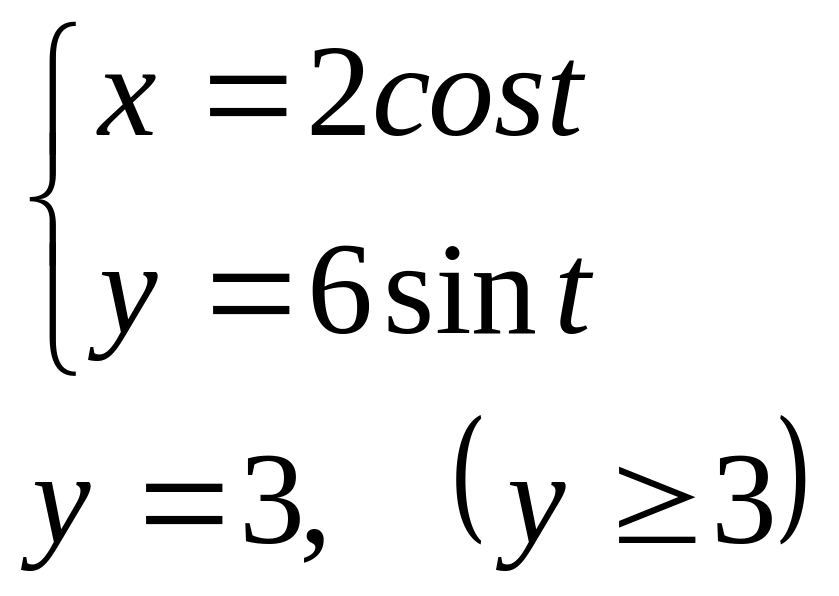 Ответ:
Ответ:
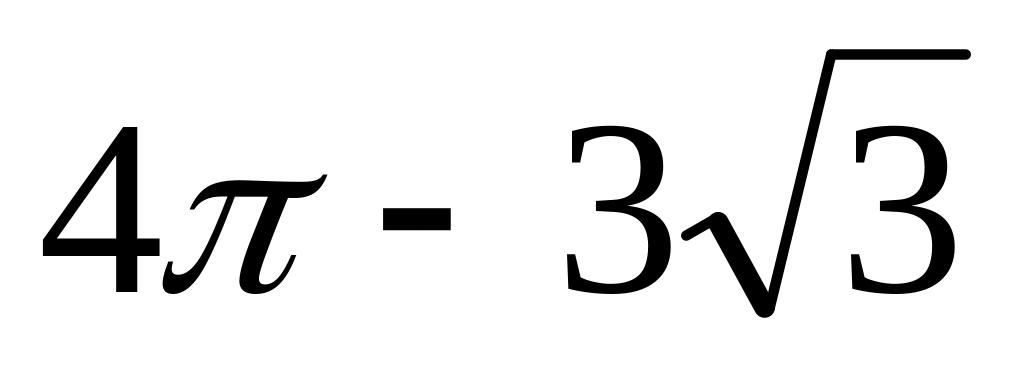
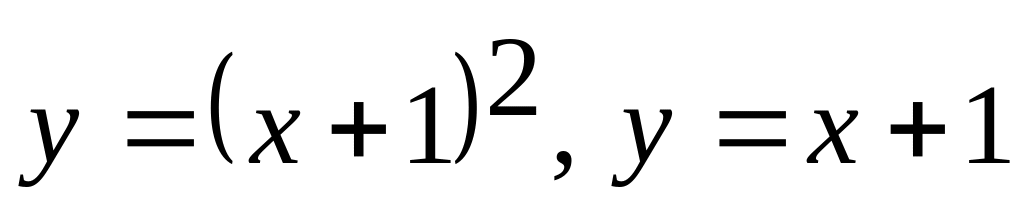
Ответ: 1/6
Ответ:3![]()
 Ответ:
9
Ответ:
9

Ответ:
![]()
Ответ: 1
Ответ:
![]()