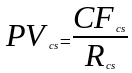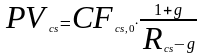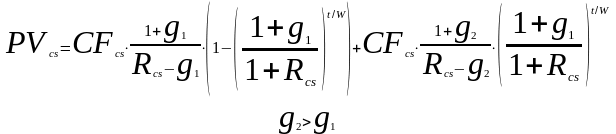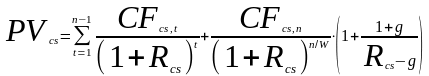Инвестиционные возможности и оценка обыкновенных акций

Обыкновенная акция – это инструмент долевого финансирования эмитента, что предопределяет характерные только для данной ценной бумаги инвестиционные свойства и управленческие возможности, которые оговариваются до начала эмиссии:

1. Должна иметь номинальную стоимость.

2. Номинальная стоимость должна быть выражена только в национальной валюте.

3. Является объектом купли-продажи.

4. Размещается только на бессрочной основе.

5. Может иметь вид на предъявителя или быть именной.

6. Эмитентами являются акционерные общества.

7. Разработка проспекта эмиссии является обязательной.

8. Держателями могут быть юридические и физические лица.

9. Держатели имеют право голосования на собраниях акционеров, а также на участие в управлении эмитентом.

10. Является необеспеченной ценной бумагой.

11. В случае ликвидации эмитента подтверждает право собственности держателя на активы эмитента, но только после удовлетворения требований кредиторов и осуществления имущественных выплат, причитающихся держателям привилегированных акций.

12. Финансовая ответственность держателя ограничена номинальной стоимостью принадлежащих ему обыкновенных акций.

13. Является неконвертируемой ценной бумагой.

14. Стоимость одной обыкновенной акции может дробиться на несколько обыкновенных акций.

15. Стоимость нескольких обыкновенных акций может консолидироваться в одну.

16. Предусматривает получение дохода (за счет чистой прибыли или за счет созданного из чистой прибыли специального фонда) в виде дивидендных платежей, величина которых не фиксируется.

17. Дивиденды выплачиваются только при наличии полной оплаты уставного капитала эмитента.

18. Выплата дохода может производиться один раз в квартал, полугодие, год.

19. Не является платежным средством.

Подчеркнем, что обыкновенная акция не гарантирует получение дивидендных платежей, в связи с чем компании, индифферентные к дивидендной политике, обеспечивают доход своим владельцам за счет роста рыночной стоимости обыкновенных акций, что признается инвесторами в качестве «заменителя» дивидендов. Тем не менее, при оценке обыкновенных акций принципиальное значение имеют величина требуемой доходности (что следует из модели дисконтированного денежного потока), а также предполагаемая стратегия выплаты дивидендов. В последнем случае речь идет о том, каким образом акционерное общество намеревается осуществлять дивидендные платежи. Рассмотрим ряд возможных случаев.

Итак, допустим, что предполагается стабильная величина дивидендного платежа, тогда приведенная (действительная) стоимость обыкновенной акции может быть рассчитана с помощью модели (10):

	(10)
где PVcs – приведенная (действительная) стоимость обыкновенной акции; CFcs – дивидендный платеж по обыкновенной акции за предполагаемый период времени (квартал, полугодие, год); Rcs – ставка требуемой доходности по обыкновенной акции за предполагаемый период времени.

Обсудим модель (10). Она фактически является копией модели (9) и представляет собой частный случай модели дисконтированного денежного потока. Отметим, как и в случае оценки бессрочной привилегированной акции, при росте величины дивидендного платежа приведенная (действительная) стоимость обыкновенной акции растет, соответственно, при росте ставки требуемой доходности приведенная (действительная) стоимость снижается.

Нередко инвесторы рассчитывают на получение растущих дивидендных платежей. Соответственно, если предполагается постоянный темп прироста дивидендов, то приведенная (действительная) стоимость обыкновенной акции рассчитывается с помощью модели (11):

	(11)
где CFcs,0 – дивидендный платеж по обыкновенной акции за отчетный период времени (квартал, полугодие, год); g – выраженный в долях единицы постоянный темп прироста дивидендов за предполагаемый период времени.

Обсудим модель (11). Прежде всего, она является частным случаем модели дисконтированного денежного потока. Отметим, как и в предыдущем случае, при росте величины дивидендного платежа приведенная (действительная) стоимость обыкновенной акции растет, соответственно, при росте ставки требуемой доходности приведенная (действительная) стоимость снижается. Причем, если предусматривается постоянный темп прироста дивидендов, то приведенная (действительная) стоимость обыкновенной акции будет больше по сравнению со случаем, когда темп прироста дивидендов не предусматривается (иначе говоря, является нулевым). Следовательно, план с приростом дивидендов будет привлекателен для потенциальных инвесторов. Кроме того, чем больше постоянный темп прироста дивидендов, тем больше приведенная (действительная) стоимость обыкновенной акции. Однако модель (11) работоспособна, когда требуемая доходность превышает темп прироста (R_cs>g), иначе оценка приведенной (действительной) стоимости принимает абсурдное значение (бесконечно большое при R_cs=g либо отрицательное при R_cs<g). Наконец, при нулевом темпе прироста дивидендов модель (11) вырождается в модель (10).

Эмитент обыкновенных акций может предложить инвесторам более сложную конфигурацию дивидендных платежей. Если в течение какого-то срока предполагается стабильная величина дивидендных платежей, а затем предусматривается выплата дивидендов с постоянным темпом прироста, то приведенная (действительная) стоимость обыкновенной акции рассчитывается с помощью модели (12):

	(12)
где t – срок до истечения стабильных по величине дивидендных платежей.

Обсудим модель (12). Она является частным случаем модели дисконтированного денежного потока, делитель (W) придает точность оценке приведенной (действительной) стоимости и его величина по-прежнему определяется принятой для исчисления единицей времени. Снова укажем, что на практике наиболее распространенной и востребованной единицей времени является день, т.е. описанный в матрице (3) 5-й случай, поскольку именно в обозначенной ситуации можно определить приведенную (действительную) стоимость обыкновенных акций на каждый день, что необходимо для совершения ежедневных сделок по их купле-продаже. Остальные же случаи (1-й, 2-й, 3-й, 4-й), описываемые матрицей (3), вряд ли востребованы для практических целей, тем не менее, теоретически вполне могут быть представлены. Важнейшей особенностью делителя по-прежнему является то, что дивидендный платеж и ставка требуемой доходности могут быть исчислены не только за год, но также за полугодие или квартал. Тогда, если предполагаемым периодом времени является полугодие, то делитель должен быть понижен в два раза (в частности, до W=0,5; 1; 2; 6; 182,5). Если же предполагаемым периодом времени является квартал, то делитель должен быть понижен в четыре раза (в частности, до W=0,25; 0,5; 3; 91,25). Наконец, рассмотрим, как изменение параметров модели (12) влияет на величину приведенной (действительной) стоимости обыкновенной акции, по которой в течение какого-то срока предполагается стабильная величина дивидендных платежей, а затем предусматривается выплата дивидендов с постоянным темпом прироста:

1. Если срок выплаты стабильных по величине дивидендов истек (т.е. при t=0), модель (12) вырождается в модель (11), при этом приведенная (действительная) стоимость обыкновенной акции возрастет, следовательно, обозначенный план выплаты дивидендов будет привлекателен для потенциальных инвесторов.

2. Чем больше величина дивидендного платежа, тем больше приведенная (действительная) стоимость обыкновенной акции.

3. Чем больше ставка требуемой доходности по обыкновенной акции за предполагаемый период времени, тем меньше ее приведенная (действительная) стоимость.

4. Чем меньше отношение срока выплаты стабильных по величине дивидендов к делителю, т.е. чем короче этот срок, тем больше приведенная (действительная) стоимость обыкновенной акции. Ценность обыкновенной акции вырастет, поскольку она размещается на бессрочной основе, и за каждый предполагаемый период времени гипотетически способна генерировать возрастающие дивидендные платежи.

5. Чем больше постоянный темп прироста дивидендов, тем больше приведенная (действительная) стоимость обыкновенной акции. Причем модель (12) работоспособна, когда требуемая доходность превышает темп прироста (R_cs>g). Иначе (при R_cs=g) оценка приведенной (действительной) стоимости принимает бесконечно большое значение либо (при R_cs<g) может принять отрицательное значение²⁰, что в любом случае абсурдно.

Акционерное общество может предложить инвесторам план с двумя стадиями дивидендных платежей, а именно: с постоянным в течение какого-то срока темпом прироста дивидендов, после чего устанавливается еще более высокий постоянный темп прироста дивидендов. В обозначенном случае приведенная (действительная) стоимость обыкновенной акции рассчитывается с помощью модели (13):

	(13)
где t – срок до истечения первой стадии дивидендных платежей; g1, g2 – выраженные в долях единицы постоянные темпы прироста дивидендов за предполагаемый период времени.

Обсудим модель (13). Снова отметим, что она является частным случаем модели дисконтированного денежного потока, делитель (W) придает точность оценке приведенной (действительной) стоимости и его величина по-прежнему определяется принятой для исчисления единицей времени. Напомним, что на практике наиболее распространенной и востребованной единицей времени является день, т.е. описанный в матрице (3) 5-й случай. Остальные случаи (1-й, 2-й, 3-й, 4-й), обозначенные в матрице (3), могут быть представлены лишь теоретически. Важнейшей особенностью делителя все также является то, что дивидендный платеж и ставка требуемой доходности могут быть исчислены не только за год, но также за полугодие или квартал. Тогда, если предполагаемым периодом времени является полугодие, то делитель должен быть понижен в два раза (в частности, до W=0,5; 1; 2; 6; 182,5). Если же предполагаемым периодом времени является квартал, то делитель должен быть понижен в четыре раза (в частности, до W=0,25; 0,5; 3; 91,25). Наконец, рассмотрим, как изменение параметров модели (13) влияет на величину приведенной (действительной) стоимости обыкновенной акции, по которой предусматривается постоянный в течение какого-то срока темп прироста дивидендов, после чего устанавливается еще более высокий постоянный темп прироста дивидендов:

1. Если темп прироста дивидендов на второй стадии окажется меньше, чем на первой стадии (т.е. при g₂<g₁) или вообще нулевым (т.е. при g₂=0), то после истечения срока выплаты дивидендов с постоянным на первой стадии темпом прироста (т.е. при t=0) модель (13) вырождается в модель (11), а приведенная (действительная) стоимость обыкновенной акции снизится. Следовательно, обозначенный план выплаты дивидендов не будет привлекателен для потенциальных инвесторов. Более того, вряд ли найдутся желающие приобрести обыкновенные акции, зная заранее о том, что они обесценятся. Значит, план с понижением темпа прироста дивидендов на второй стадии, скорее всего, является практически не реализуемым.

2. Если темпы прироста на обеих стадиях совпадают по величине (т.е. при g₂=g₁), то модель (13) фактически совпадет с моделью (11), а приведенная (действительная) стоимость обыкновенной акции не изменится.

3. Если (при g₂>g₁) срок выплаты дивидендов с постоянным на первой стадии темпом прироста истек (т.е. при t=0), модель (13) вырождается в модель (11), при этом приведенная (действительная) стоимость обыкновенной акции возрастет, следовательно, обозначенный план выплаты дивидендов будет привлекателен для потенциальных инвесторов.

4. Чем больше величина дивидендного платежа, тем больше приведенная (действительная) стоимость обыкновенной акции.

5. Чем больше ставка требуемой доходности по обыкновенной акции за предполагаемый период времени, тем меньше ее приведенная (действительная) стоимость.

6. Чем меньше (при g₂>g₁) отношение срока до истечения первой стадии дивидендных платежей к делителю, т.е. чем короче этот срок, тем больше приведенная (действительная) стоимость обыкновенной акции. Ценность обыкновенной акции вырастет, поскольку она, как уже отмечалось, размещается на бессрочной основе, и за каждый предполагаемый период времени гипотетически способна генерировать возрастающие дивидендные платежи.

7. Чем больше постоянный темп прироста дивидендов, тем больше приведенная (действительная) стоимость обыкновенной акции. Причем модель (13) работоспособна, когда требуемая доходность превышает темп прироста (R_cs>g₂, R_cs>g₁). Иначе (при R_cs=g₂ и/или при R_cs=g₁) оценка приведенной (действительной) стоимости принимает бесконечно большое значение либо (при R_cs<g₂ и/или при R_cs<g₂ в сочетании с R_cs<g₁) может принять отрицательное значение²¹, что в любом случае абсурдно.

Наконец, акционерное общество может предложить инвесторам план, в соответствии с которым дивидендные платежи в течение какого-то срока носят нерегулярный характер, после чего предполагается выплата дивидендов с постоянным темпом прироста. Тогда приведенная (действительная) стоимость обыкновенной акции определяется на основе модели (14):

(14)

где CFcs,t – дивидендный платеж по обыкновенной акции за предполагаемый период времени t (квартал, полугодие, год); CFcs,n – дивидендный платеж по обыкновенной акции за предполагаемый период времени n (квартал, полугодие, год); t=1, …, n-1 – целое число периодов времени, оставшихся до окончания срока, в течение которого дивидендные платежи носят нерегулярный характер; n – оставшийся до окончания срок, в течение которого дивидендные платежи носят нерегулярный характер.

Обсудим модель (14). В очередной раз укажем, что она является частным случаем модели дисконтированного денежного потока, делитель (W) придает точность оценке приведенной (действительной) стоимости и его величина по-прежнему определяется принятой для исчисления единицей времени. Повторим, что на практике наиболее распространенной и востребованной единицей времени является день, т.е. описанный в матрице (3) 5-й случай. Остальные случаи (1-й, 2-й, 3-й, 4-й), обозначенные в матрице (3), могут быть представлены лишь теоретически. Важнейшей особенностью делителя, как уже отмечалось, является то, что дивидендный платеж и ставка требуемой доходности могут быть исчислены не только за год, но также за полугодие или квартал. Тогда, если предполагаемым периодом времени является полугодие, то делитель должен быть понижен в два раза (в частности, до W=0,5; 1; 2; 6; 182,5). Если же предполагаемым периодом времени является квартал, то делитель должен быть понижен в четыре раза (в частности, до W=0,25; 0,5; 3; 91,25). Наконец, рассмотрим, как изменение параметров модели (14) влияет на величину приведенной (действительной) стоимости обыкновенной акции, по которой дивидендные платежи в течение какого-то срока носят нерегулярный характер, после чего предполагается выплата дивидендов с постоянным темпом прироста:

1. Если срок выплаты носящих нерегулярный характер дивидендов истек, модель (14) вырождается в модель (11), при этом приведенная (действительная) стоимость обыкновенной акции возрастет, конечно, при условии, что дивидендный платеж за последний период времени (CF_cs,n) не планируется явно заниженным²², следовательно, обозначенный план выплаты дивидендов будет привлекателен для потенциальных инвесторов.

2. Чем больше величина дивидендного платежа, тем больше приведенная (действительная) стоимость обыкновенной акции.

3. Чем больше ставка требуемой доходности по обыкновенной акции за предполагаемый период времени, тем меньше ее приведенная (действительная) стоимость.

4. Чем меньше отношение срока, в течение которого дивидендные платежи носят нерегулярный характер к делителю, т.е. чем короче этот срок, тем больше приведенная (действительная) стоимость обыкновенной акции. Ценность обыкновенной акции вырастет, поскольку она, как уже не раз отмечалось, размещается на бессрочной основе, и за каждый период времени гипотетически способна генерировать возрастающие дивидендные платежи. Еще раз укажем, что это возможно, если величина дивидендного платежа за последний период времени (CF_cs,n) не планируется явно заниженной.

5. Чем больше постоянный темп прироста дивидендов, тем больше приведенная (действительная) стоимость обыкновенной акции. Причем модель (14) работоспособна, когда требуемая доходность превышает темп прироста (R_cs>g). Иначе (при R_cs=g) оценка приведенной (действительной) стоимости принимает бесконечно большое значение либо (при R_cs<g) может принять отрицательное значение²³, что в любом случае абсурдно.

Напоследок обсудим дополнительные возможности и последствия, возникающие при эмиссии обыкновенных акций, однако, прежде всего, укажем на обязательные ограничения:

1. Обыкновенные акции эмитента торгуются на фондовой бирже.

2. Обыкновенные акции имеют номинальную стоимость.

В случае эмиссии обыкновенных акций, напомним, всегда размещаемых на бессрочной основе, особенно уместно подчеркнуть, когда не предусматривается их погашение по номинальной стоимости, обозначенный параметр не имеет никакого значения, т.к. фактически не является денежным потоком. Можно сказать, что номинальная стоимость обыкновенной акции указывается лишь формально, в силу требований закона, однако в качестве денежного потока она имеет нулевую ценность, следовательно, никак не влияет на величину приведенной (действительной) стоимости обыкновенной акции.

Если цена продажи обыкновенной акции в ходе дополнительной эмиссии окажется выше приведенной (действительной) стоимости, которая численно совпадает с номинальной стоимостью обыкновенной акции дополнительного выпуска, а также с рыночной ценой обыкновенной акции, находящейся в обращении, то это вызовет одобрение держателей обыкновенных акций, находящихся в обращении, т.к. рыночная стоимость обыкновенных акций, находящихся в обращении, предположительно вырастет из-за перелива части стоимости собственного капитала, распределенного в обыкновенных акциях дополнительного выпуска, в пользу держателей обыкновенных акций, находящихся в обращении²⁴. Если цена продажи обыкновенной акции в ходе дополнительной эмиссии окажется ниже приведенной (действительной) стоимости, которая численно совпадает с номинальной стоимостью обыкновенной акции дополнительного выпуска, а также с рыночной ценой обыкновенной акции, находящейся в обращении, то это вызовет недовольство держателей обыкновенных акций, находящихся в обращении, т.к. рыночная стоимость обыкновенных акций, находящихся в обращении, предположительно снизится из-за перелива части стоимости собственного капитала, распределенного в обыкновенных акциях, находящихся в обращении, в пользу держателей обыкновенных акций дополнительного выпуска²⁵. Отметим, что продажа обыкновенной акции в ходе дополнительной эмиссии по цене ниже номинальной стоимости допускается в исключительных случаях, соответственно, благоразумные держатели обыкновенных акций, находящихся в обращении (иначе говоря, прежних выпусков), как правило, этого не допускают, пресекая тем самым ущемление собственных финансовых интересов.

Выводы

Ценные бумаги имеют двойственную экономическую природу, являясь одновременно инструментом финансирования эмитента и финансовым активом держателя. Причем это относится к рыночным ценным бумагам, которые имеют ценность благодаря возможности генерировать доходы. Отсюда объективно возникает необходимость оценки потенциальных доходов и вместе с ними ценных бумаг. Очевидно, что возможность получения доходов не является гарантированной, поэтому сформировалась учитывающая данный фактор парадигма оценки ценных бумаг, математически формализованная в модели дисконтированного денежного потока. Обозначенная модель, являющаяся базовой при оценке финансовых активов, имеет целый ряд частных случаев, предназначенных для оценки акций и облигаций. Каждый случай оценки ценных бумаг исходит из уникальности их свойств. Однако все модели позволяют получить оценку приведенной (действительной) стоимости ценных бумаг, причем названная оценка может оказаться рассогласованной с рыночными курсами ценных бумаг, что предоставляет их держателям специфические инвестиционные возможности. Отметим, что облигации, привилегированные акции и обыкновенные акции являются, с точки зрения процедуры оценки, независимыми объектами. Тем не менее, при эмиссии облигации, а также привилегированные и обыкновенные акции дополнительных выпусков могут существенно влиять на рыночную стоимость обыкновенных акций, находящихся в обращении. Этот феномен объясняется переливом капитала от держателей одних ценных бумаг к держателям других, конечно, при условии, что обозначенные ценные бумаги выпущены одним эмитентом. Причем возникновение феномена перелива капитала не зависит от способа оценки ценных бумаг. Если результат перелива ощущают держатели обыкновенных акций, находящихся в обращении, то именно держателям обыкновенных акций, находящихся в обращении, отводится ключевая роль при определении параметров эмиссии облигаций, а также привилегированных и обыкновенных акций дополнительных выпусков. Кроме того, на держателей обыкновенных акций, находящихся в обращении (т.е. прежних выпусков), ложится ответственность за соблюдение интересов держателей облигаций, а также за соблюдение интересов держателей привилегированных акций. Держатели обыкновенных акций обязаны исходить из предположения, что соблюдение и защита финансовых интересов держателей облигаций, а также соблюдение и защита финансовых интересов держателей привилегированных акций выгодны самим держателям обыкновенных акций. Иначе курс находящихся в обращении обыкновенных акций снизится из-за перелива капитала в результате понижения оценки облигаций и/или привилегированных акций дополнительных выпусков. Однако, если рассматривать облигации, привилегированные акции и обыкновенные акции как отдельно взятые (независимые) объекты, то применение разнообразных форматов выплаты дохода и изъятия из обращения (например, в результате оговариваемого в проспекте эмиссии выкупа) способствует повышению их инвестиционной привлекательности для потенциальных держателей. Для эмитента это полезно с точки зрения расширения возможностей финансирования.