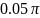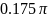Найти коэффициенты системы
- частотная характеристика ЛПП-системы
с импульсной характеристикой
.
Частотная
характеристика
является
непрерывной функцией частоты. Кроме
того, это периодическая функция частоты
с периодом
.
Поскольку - периодическая функция частоты, она может быть представлена в виде ряда Фурье :
В этой формуле коэффициентами Фурье являются значения импульсной характеристики .
Ряд Фурье (прямое преобразование Фурье)
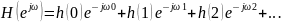
Используя
формулу Эйлера:
выражение (4) можно записать:
Построить ачх и фчх системы
В общем случае – комплексная функция и может быть выражена через свои действительную и мнимую части
или через модуль и фазу
Амплитудно-частотная характеристика – АЧХ
Фазо-частотная характеристика – ФЧХ
Используя
выражение (5) запишем выражения для
действительной и мнимой части частотной
характеристики
С
учетом того, что частотная характеристика
является непрерывной функцией частоты
с периодом
для построения графиков АЧХ и ФЧХ
вычислим значения на интервале
.
Зададим
изменяющуюся на интервале
с шагом
Расчет действительной части комплексной функции :
Расчет мнимой части комплексной функции :
Расчет АЧХ комплексной функции :
Расчет ФЧХ комплексной функции :
При расчетах использовали программу MathCad. Результаты расчетов приведены в Таблице 1.
Таблица 1.
|
|
|
|
|
|
0.5 |
0 |
0.5 |
0 |
|
0.472 |
-0.178 |
0.505 |
-0.36 |
|
0.391 |
-0.339 |
0.518 |
-0.715 |
|
0.264 |
-0.469 |
0.538 |
-1.059 |
|
0.101 |
-0.555 |
0.564 |
-1.391 |
|
-0.082 |
-0.588 |
0.594 |
1.432 |
|
-0.27 |
-0.564 |
0.626 |
1.124 |
|
-0.447 |
-0.484 |
0.659 |
0.826 |
|
-0.594 |
-0.353 |
0.691 |
0.535 |
|
-0.7 |
-0.18 |
0.723 |
0.251 |
|
-0.754 |
0.022 |
0.754 |
-0.029 |
|
-0.747 |
0.237 |
0.784 |
-0.307 |
|
-0.68 |
0.447 |
0.814 |
-0.582 |
|
-0.554 |
0.637 |
0.844 |
-0.855 |
|
-0.376 |
0.79 |
0.875 |
-1.126 |
|
-0.159 |
0.895 |
0.909 |
-1.395 |
|
0.085 |
0.94 |
0.944 |
1.48 |
|
0.34 |
0.923 |
0.983 |
1.218 |
|
0.587 |
0.84 |
1.025 |
0.961 |
|
0.812 |
0.697 |
1.07 |
0.709 |
|
1 |
0.5 |
1.118 |
0.464 |
|
1.139 |
0.261 |
1.168 |
0.225 |
|
1.22 |
-7.05e-3 |
1.22 |
-5.78e-3 |
|
1.239 |
-0.289 |
1.272 |
-0.229 |
|
1.194 |
-0.571 |
1.324 |
-0.446 |
|
1.09 |
-0.837 |
1.374 |
-0.655 |
|
0.931 |
-1.075 |
1.422 |
-0.857 |
|
0.728 |
-1.274 |
1.467 |
-1.052 |
|
0.489 |
-1.427 |
1.509 |
-1.241 |
|
0.227 |
-1.529 |
1.546 |
-1.423 |
|
-0.046 |
-1.578 |
1.579 |
1.541 |
|
-0.321 |
-1.574 |
1.607 |
1.37 |
|
-0.585 |
-1.522 |
1.63 |
1.204 |
|
-0.833 |
-1.424 |
1.65 |
1.042 |
|
-1.055 |
-1.288 |
1.665 |
0.884 |
|
-1.249 |
-1.12 |
1.677 |
0.731 |
|
-1.41 |
-0.925 |
1.686 |
0.58 |
|
-1.537 |
-0.71 |
1.693 |
0.433 |
|
-1.627 |
-0.481 |
1.697 |
0.287 |
|
-1.682 |
-0.243 |
1.699 |
0.143 |
|
-1.7 |
0 |
1.7 |
0 |
Построим АЧХ и ФЧХ цифрового фильтра (с использованием программы MathCad).
Рис. 5. График АЧХ цифрового фильтра
Рис. 6. График ФЧХ цифрового фильтра