5.1. Примеры решения задач

Пример 1. По двум бесконечно длинным прямым параллельным проводникам, расстояние между которыми d=15 см, текут токи I₁=70 A и I₂=50 А в противоположных направлениях (рис. 21). Найти магнитную индукцию В в точке А удаленной на r₁=20 см от первого и r₂=30 см от второго проводника.

Решение. Согласно принципу суперпозиции полей магнитной индукции в точке А равна векторной сумме магнитных индукций, созданных каждым током в отдельности:

.

Рис. 21

Модуль вектора В на основании теоремы косинусов равен

,

. (1)

Вычислим . По теории косинусов запишем

,

где – расстояние между проводами. Отсюда

^.

Значения индукций и найти по формулам

; .

Подставив значения и в формулу (1), получим

Пример 2. Найти индукцию магнитного поля в центре проволочной квадратной рамки со стороной а=15 см, если по рамке течет ток I=5 А.

Решение. Искомая магнитная индукция является векторной суммой индукции ; ; ; , создаваемых токами, текущими в каждом из четырех проводов, являющихся сторонами квадрата, т.е. = + + + или =4 .

Магнитная индукция поля создаваемого отрезком проводника выражается формулой

где I – сила тока в проводнике, r= – расстояние от проводника до точки поля, в которой надо определить индукцию.

Так как направление всех векторов одинаково, то модуль вектора будет

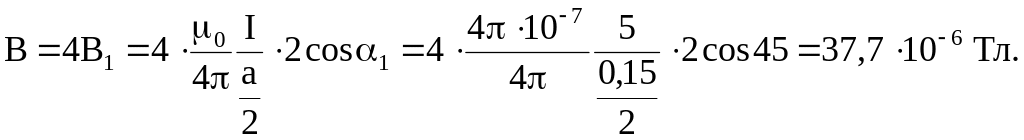
Пример 3. По прямому горизонтально расположенному проводу протекает ток I₁=10 А (рис. 22). Под ним на расстоянии см находится параллельный ему алюминиевый провод по которому пропускают ток I₂=1,5 А. Найти, какой должна быть площадь поперечного сечения алюминиевого провода, чтобы он удерживался незакрепленным. Плотность алюминия .

Решение. Верхний проводник действует на нижний с силой

. (1)

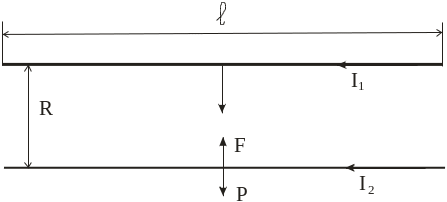
Рис. 22

Нижний провод будет свободно висеть только в том случае, если его вес компенсируется силой F притяжения со стороны верхнего провода:

F=P или , (2)

где – длина провода.

, (3)

где – плотность алюминия, s – площадь поперечного сечения провода, q – ускорение свободного падения.

Подставив в формулу (2), (1) и (3) получим

,

где μ₀ – магнитная постоянная, ; μ − относительная магнитная проницаемость воздуха, .

Тогда S = .

Пример 4. Плоский квадратный контур со стороной а=10 см, по которому течет ток силой 100 А, свободно установился в однородном магнитном поле с индукцией В=1 Тл. Найти работу, совершаемыми внешними силами при повороте контура относительно оси, проходящей через середину его противоположных сторон на угол . При повороте контура сила тока в нем поддерживается неизменной.

Решение. На контур с током в магнитном поле действует механический момент

М= (1)

По условию задачи, в начальном положении контур свободно установившийся в магнитном поле (М=0), а значит , т. е. векторы совпадают по направлению. Если внешние силы выведут контур из положения равновесия, то возникнет момент сил, определенной формулой (1), будет стремиться возвратить контур в исходное положение. Против этого момента и будет совершаться работа внешними силами.

(2)

Подставив сюда выражение М по формуле (1) и учтя, что , где I – сила тока в контуре, S= – площадь контура, получим

Взяв интеграл от этого выражения, найдем работу при повороте на конечный угол :

Дж.

Пример 5. Электрон ускоренный разностью потенциалов U=6 кВ, влетает в однородное магнитное поле под углом и начинает двигаться по винтовой линии (рис. 23). Индукция магнитного поля В=1,310 Тл. Найти радиус R витка и шаг h винтовой линии.

Решение. Так как магнитное поле направлено под углом к скорости электрона, то дальнейшее его движение представляет геометрическую сумму двух одновременных движений: вращение по окружности со скоростью в плоскости, перпендикулярной силовым линиям, и перемещения вдоль поля со скоростью . В результате одновременного участия в движениях по окружности и по прямой электрон будет двигаться по винтовой линии.

Рис. 23

Сила Лоренца F сообщает электрону нормальное ускорение. По второму закону Ньютона , где F= и . Тогда

.

Следовательно, радиус винтовой линии равен

. (1)

Подставив значения величин m, v, е, В и α и произведя вычисления, получим

R=0,19 мм.

Шаг винтовой линии равен пути, пройденному электроном вдоль поля со скоростью v_х за время, которое понадобится электрону для того, чтобы совершить один оборот:

h=v_xT=v·cosα·T, (2)

где − период вращения электрона. Подставив это выражение для Т в формулу (2), найдем

.

Подставив в эту формулу значения величин π, R и α и вычислить, получим

h=2,06 мм.