9.4.3 Мала вибірка.

На практиці часто мають місце малі вибірки (n<30) – контроль якості продукції, при якому дослідні зразки знищуються. Вибірки невеликого обсягу мають свої особливості у порівнянні, з методами великих вибірок.

Ст'юдент (дійсно В. Госсет) встановив закон розподілу відхилень вибіркових характеристик від генеральних для малих вибірок (так званий t – розподіл Ст'юдента, що подібний для нормального закону).

Відхилення вибіркової середньої від генеральної середньої – Ст'юдент виразив у вигляді відношення Cт'юдента.

Фактично це коефіцієнт довіри між граничністю та середньої квадратичною похибками у малій вибірці

Значення t може бути знайдено за математичними таблицями розподілу Ст'юдента в залежності від рівня значимості а= 1- Р (Р – рівень ймовірності) і числа ступенів вільності варіації

К = n -1 (п – обсяг малої вибірки).

Середня квадратична помилка для кількостей ознаки малої вибірки визначається як:

,

де – дисперсія малої вибірки:

.

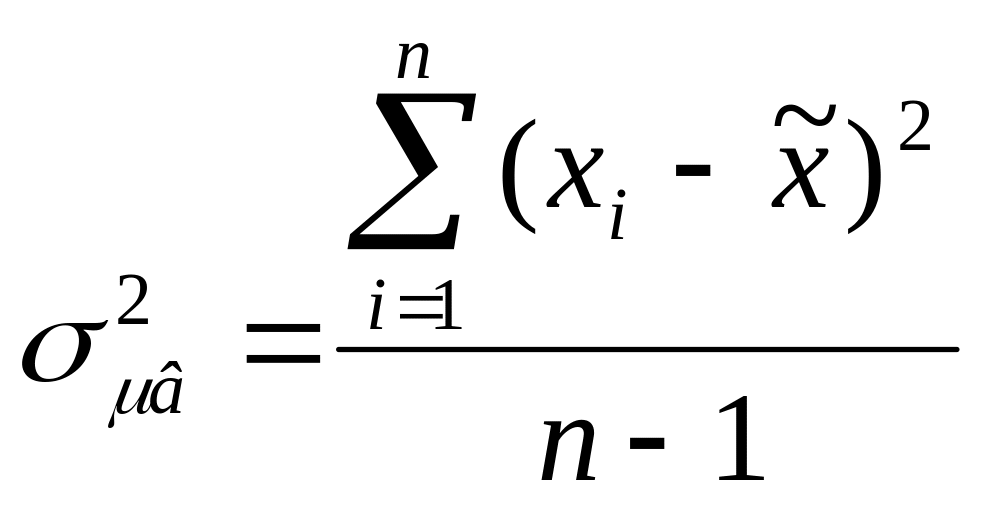Ймовірність того, що помилка вибірки буде не більше заданого значення являє собою функцію S (t, n ) наведену в таблицях Ст'юдента в літературі з математичної статистики:

Таблиці Ст'юдента свідчать, що при збільшенні обсягу вибірки розподіл Ст'юдента наближуються до нормального закону і при n = 20 він мало відрізняється від нормального розподілу. Приклад. Визначення помилки при випадковому безповторному відборі методом малої вибірки.

На зерноприймальному пункті формуються партії зерна для подальшого його сушіння. Для встановлення режиму роботи зерносушарки необхідно знати вологість зерна, яка буде встановлена впродовж дня взяттям вибірково 10 проб з автомашин із зерном.

Номер проби	1	2	3	4	5	6	7	8	9	10
Вологість зерна, %	18,4	17,8	18,0	17,5	17,7	18,8	19,	17,9	18,6	18,7

Визначити :

1. середню вологість зерна пшениці за вибірковою сукупністю;

2. середню та граничну помилки вибіркової середньої;

3. межі, в яких з ймовірністю 0,954 перебуває середня вологість зерна у генеральній сукупності.

Зробити висновки.

Таблиця 9.4. – Розрахунок середньої вологості зерна та дисперсії малої

вибірки

1	18,4	0,16	0,026
2	17,8	-0,44	0,194
3	18,0	-0,24	0,058
4	17,5	-0,74	0,547
5	17.7	-0,54	0,292
6	18,8	0,56	0,314
7	19,0	0,76	0,577
8	17,9	-0,34	0,115

Продовження табл. 9.4.

9	18,6	0,36	0,130
10	18,7	0,46	0,211
Разом	182,4	х	2,274

1.Середнє значення вологості зерна пшениці за даними таблиці:

.

За даними таблиці розраховуємо вибіркову дисперсію:

.

2. Середня квадратична похибка вибірки дорівнює:

.

Отже вибіркова середня = 18 24% є оцінкою генеральної середньої з середньою похибкою .

При заданому рівні ймовірності Р=0,954 коефіцієнт довіри t при малій вибірці може бути визначено з використанням математичних таблиць розподілу Ст'юдента, які є в навчальній літературі: t = 2,26 при рівні значимості - 0,05 та числі ступенів вольності К = п- 1 = 10-1 =9.

Тоді гранична похибка вибірки дорівнює

3. Встановимо інтервальну оцінку середньої вологості зерна пшениці в генеральній сукупності .

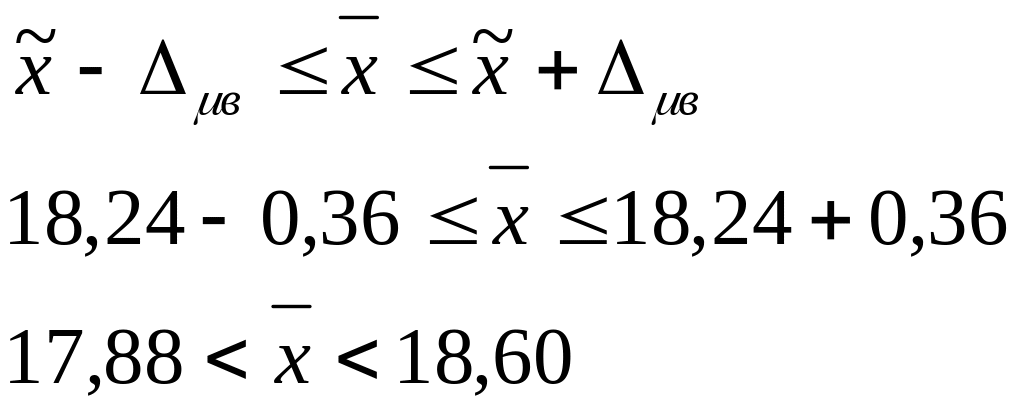
Таким чином, з ймовірністю 0,954 можна стверджувати, що середня вологість зерна в генеральній сукупності перебуває в інтервалі від 17,88% до 18,60%.