6.4.Поняття множинної кореляції

Парна кореляція або парна регресія можуть розглядатися як окремий випадок відображення зв`язку деякої залежної змінної, з однієї сторони, та однієї з багатьох незалежних змінних – з другої. Коли ж потрібно охарактеризувати зв`язок всієї множини незалежних змінних з результативною ознакою, то ведуть мову про множинну кореляцію або множинну регресію.

Для встановлення зв`язку при багатофакторній кореляції використовуються багатофакторні математичні моделі множинної кореляції, серед яких слід відзначити такі:

лінійні ;

ступеневі ;

логарифмічні ,

де у – результативна ознака,

– факторна ознака.

Наведені моделі зручні тим, що їх параметри – економічно інтерпретуються. В лінійній моделі коефіцієнт при невідомих є коефіцієнтом регресії, який показує, на скільки одиниць (збільшиться – зменшиться) функція при зміні аргументу (фактора) на одну одиницю при незмінних значеннях інших факторів.

В ступеневих і логарифмічних моделях коефіцієнт є коефіцієнтом еластичності і показує на скільки процентів зміниться функція при зміні аргументу (фактора) на один процент при фіксованому значенні решти факторів.

Відповідність рівняння процесу, що досліджується оцінюється за допомогою ряду статистичних характеристик –коефіцієнт множинної кореляції, β-коефіцієнти, критерій Стьюдента.

Найбільш важливою характеристикою моделі є коефіцієнт множинної кореляції R, квадрат якого представляє собою коефіцієнт детермінації D. Його рівень показує долю впливу введених в модель факторів на зміну рівня результативної ознаки. Чим більше значення коефіцієнту множинної кореляції, тим вище якість рівняння.

Тема 7. Ряди динаміки

7.1. Суть, складові елементи та види рядів динаміки

Суспільні явища безперервно змінюються. Одне з основних завдань статистики заключається у вивченні поступального розвитку і змін суспільних явищ і процесів. Вирішується воно на основі побудови та аналізу динамічних рядів.

Динамічний ряд або ряд динаміки – це ряд розміщених у хронологічній послідовності чисел, які характеризують зміну того чи іншого соціально-економічного явища за певний період часу. Будь який динамічний ряд складається з двох елементів – рівнів часу та рівнів ряду. Рівні часу – це перелік хронологічних дат (моментів) або інтервалів часу. Рівні ряду – це конкретні значення відповідних статистичних показників.

При вивченні динаміки важливі не лише числові значення рівнів, але і послідовність їх. Як правило, часові інтервали поміж рівнями однакові (доба, декада, місяць, квартал, рік). Приймаючи будь який інтервал за одиницю, послідовність рівнів можна записати так: – число рівнів ( довжина динамічного ряду).

Залежно від статистичної природи показника – рівня розрізняють динамічні ряди первинні і похідні, ряди абсолютних, відносних, середніх величин.

За ознакою часу існують динамічні ряди двох видів: інтервальні та моментні.

В інтервальних рядах рівні ряду характеризуються розвитком суспільного явища впродовж певного періоду часу (річне виробництво продукції в розрізі місяців, кварталів; виробництво продукції впродовж п'яти, десяти років тощо).

Прикладом інтервального ряду динаміки є виробництво безалкогольних напоїв в Україні за 2000 – 2005рр (млн. дал.).

Таблиця 7.1 – Виробництво безалкогольних напоїв в Україні

Рік	2000	2001	2002	2003	2004	2005
Виробництво безалкогольних напоїв, млн. дал.	67,4	85,3	114,0	125,0	140,0	169,0

Рівні інтервальних рядів – це результативні показники, що відповідають ін­тервалу часу. їх можна підсумовувати та ділити, отримувати середній рівень.

Моментний – це динамічний ряд, рівень якого фіксує стан явища на певний момент часу (дату). Прикладом моментного ряду динаміки можуть бути виробни­чі запаси підприємства за рік.

Таблиця 7.2. Виробничі запаси підприємства.

Моменти часу	1.01 звітного року	1.04	1.07	1.10	1.1 наступного року
Вартість виробничих запасів, тис. грн...	1350	1480	1930	1700	1550

Рівні моментного ряду підсумуванню не підлягають, так як існує повторний рахунок в рівнях. В той же час можливим є розрахунок різниць рівнів цього ряду, що свідчить про зміну рівня за певний проміжок часу.

У рядах рівні яких варіюють, виникає потреба обчислення сталої, типової для даного періоду характеристики. Такою характеристикою є середній рівень.

Методи обчислення середніх рівнів динамічних рядів залежать від статистичної структури показника.

В інтервальному ряді, рівні якого динамічно адитивні, використовують середню арифметичну просту.

,

де n – число рівнів ряду.

Так, використовуючи дані табл. 7.1 Можливо розрахувати середньорічне виробництво безалкогольних напоїв за період 2000 – 2005 рр, яке дорівнює 116,78 млн. дол. (700,7 : 6).

Сума рівнів моментного ряду сама по собі не має економічного змісту, тому розрахунок середнього рівня моментного ряду здійснюється за формулою середньої хронологічної:

.

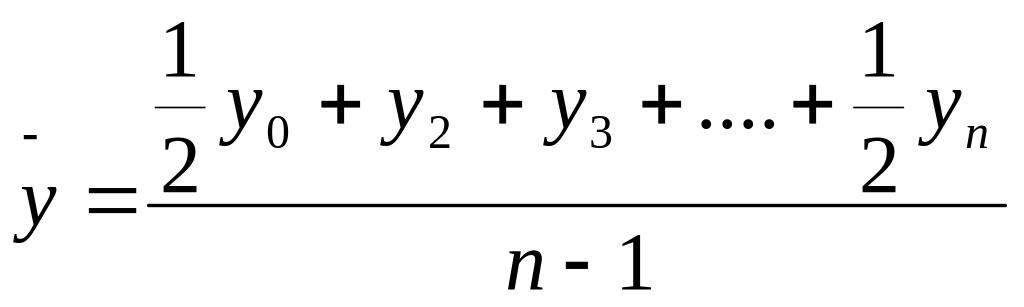Використовуючи цю формулу визначимо по даних табл. 7.2 середньорічні виробничі запаси підприємства:

.

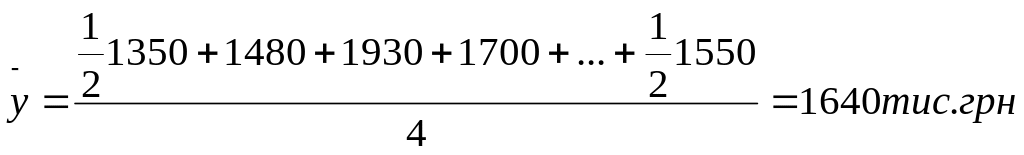Для моментного ряду , в якому є лише інформація про стан явища на початок і кінець періоду середній рівень може бути розрахований як просто середня арифметична

де – рівні на початок і кінець періоду.

В такий спрощений спосіб можна розрахувати по формах річної звітності середньорічну вартість основних засобів, оборотних коштів.

Ряди динаміки поділяють на одномірні та багатомірні.

Одномірні характеризують зміну одного показника (виробництво цукру), багатомірні – двох, трьох і більше показників.

Багатомірні динамічні ряди, у свою чергу поділяються на види: паралельні та ряди взаємозв'язаних показників.

Паралельні відображають динаміку:

або одного і того самого показника, щодо різних об'єктів (виробництво цукру на заводах об'єднання тощо);

або різних показників щодо одного і того самого об'єкта (виробництво основних продуктів харчування в області).

Зв'язок між показниками багатомірного динамічного ряду може бути функціональним (адитивним чи мультиплікативним) або кореляційним.

Прикладом адитивно зв'язаних рядів є динаміка цілого і його складових частин (чисельність фахівців, що мають науковий ступінь в тому числі доктора наук, кандидата наук). Прикладом мультиплікативно зв'язаних – динаміка посівної площі, врожайності і валового збору сільськогосподарської культури.

Прикладом кореляційно зв'язаних рядів – динаміка фондоозброєності і продуктивності праці.

Аналіз динаміки суспільних явищ, як правило здійснюється на основі багатомірних динамічних рядів.

Динамічні ряди економічних показників в більшості своїй нестандартні, їм притаманна тенденція, яка відображує динамічність економіки.

Зростання виробничих ресурсів, структурні зміни, підвищення технічного рівня призводять до інтенсивної зміни факторів зростання, посилюють динамічність соціально-економічних процесів.

Поряд з динамічністю економічні процеси мають таку властивість, як інерційність, тобто якийсь час зберігається механізм формування явищ і характер розвитку (темпи, напрями тощо). При значній інерційності процесу і незмінності комплексу умов його розвитку правомірно очікувати в майбутньому такий характер розвитку, який було виявлено у минулому. Саме в цьому вбачається принципова можливість статистичного прогнозування соціально-економічного розвитку.