6.3.Оцінка щільності
Оцінка щільності зв'язку – це оцінка узгодженості варіації взаємозв'язаних ознак. Для оцінювання щільності зв'язку статистика використовує низку коефіцієнтів з такими спільними властивостями:
за відсутності будь-якого зв'язку значення коефіцієнта наближається до нуля, при функціональному зв'язку – до одиниці;
за наявності кореляційного зв'язку коефіцієнт виражається дробом, який за абсолютною величиною тим більший, чим щільніший зв'язок.
Для лінійного зв'язку використовується лінійний коефіцієнт кореляції Пірсона – r. Обчислення лінійного коефіцієнта кореляції – r ґрунтується на відхиленнях значень взаємозв'язаних ознак х і у від середніх:
За даними табл. 6.2:
Величина коефіцієнта кореляції свідчить про досить значний вплив кількості внесених добрив на врожайність зернових. Коефіцієнт кореляції характеризує не тільки щільність, а й напрям зв`язку. Додатнє значення свідчить про прямий зв`язок, а від'ємне – про зворотній.
Знаки коефіцієнтів кореляції і регресії однакові, величини їх взаємозв'язані функціонально:
;
;
Завдяки цьому один коефіцієнт можна обчислити, знаючи інші
;
Вимірювання
щільності нелінійного зв'язку групується
у
співвідношенні варіацій теоретичних
та емпіричних (фактичних) значень
результативної ознаки у.
Як відомо, відхилення індивідуального
значення ознаки у
від
середньої
можна розкласти на дві складові.
У
регресійному аналізі це відхилення
лінії регресії від середньої
,
то
є наслідком дії фактора х
та відхилення фактичного значення від
лінії регресії
,
що є наслідком дії інших факторів.
Взаємозв'язок факторної та залишкової варіації описується правилом декомпозиції варіації:
,
де:
– загальна
дисперсія ознаки – у;
–
факторна
дисперсія;
–
залишкова
дисперсія.
Значення
факторної дисперсії
буде тим більшим, чим сильніший вплив
фактора х
на результат у.
Відношення факторної дисперсії до загальної розглядається як міра щільності кореляційного зв’язку і називається коефіцієнтом детермінації:
За попередніми розрахунками:
то
,
або
.
Коефіцієнт детермінації становить:
,
тобто 84,3% варіації врожайності зернових залежить від варіації кількості внесених добрив, а 15,7% припадає на інші фактори.
Корінь квадратний з коефіцієнта детермінації називають індексом кореляції R. Коли зв’язок лінійний R=|r|, що підтверджують обчислення:
.
Тому за відомим лінійним коефіцієнтом кореляції r можна визначити внесок ознаки х-у варіацію у. Так при r = 0,8 можна сказати, що 64% варіації у залежить від варіації х.
У моделі аналітичного групування мірою щільності зв’язку є відношення міжгрупової дисперсії до загальної, яке називають кореляційним відношенням:
,
де
–
міжгрупова дисперсія, яка вимірює
варіацію ознаки у
під впливом тільки груповальної ознаки
х;
–
загальна
дисперсія, яка вимірює варіацію
результативної ознаки у,
зумовлену впливом всіх можливих факторів.
Кореляційне
відношення коливається від 0 до 1, а якщо
подається в процентах, то від 0 до 100%. За
відсутнього зв’язку
,
а за умови функціонального –
.Чим
більше
наближається до одиниці, тим щільніший
зв’язок.
Застосуємо кореляційне відношення для оцінки щільності зв’язку між розміром МТК і продуктивністю праці (див. табл.6.3 та 6.4). Розрахунок загальної та факторної дисперсії показано нижче. Згідно з розрахунками загальна дисперсія становить 4,41, а факторна 2,69.
Таблиця 6.3 – (до розрахунку загальної дисперсії продуктивності праці
(
))
Продуктивність праці, тонн молока на 1 особу |
до 10 |
10-12 |
12-14 |
14-16 |
16 і більше |
Разом |
Кількість
господарств - |
5 |
11 |
25 |
18 |
6 |
65 |
|
9 |
11 |
13 |
15 |
17 |
х |
|
-4,3 |
-2,3 |
-0,3 |
1,7 |
3,7 |
х |
|
92,4 |
58,2 |
2,2 |
52,0 |
82,1 |
286,9 |
Таблиця 6.4 (до розрахунку загальної дисперсії продуктивності праці
( ))
Кількість корів,голів |
|
|
|
|
До 200 |
9 |
10,1 |
-3,2 |
92,16 |
200-400 |
28 |
12,8 |
-0,5 |
7,00 |
400-600 |
21 |
14,3 |
1 |
21,00 |
600 і більше |
7 |
16,1 |
2,8 |
54,88 |
По сукупності в цілому |
65 |
13,3 |
X |
175,04 |
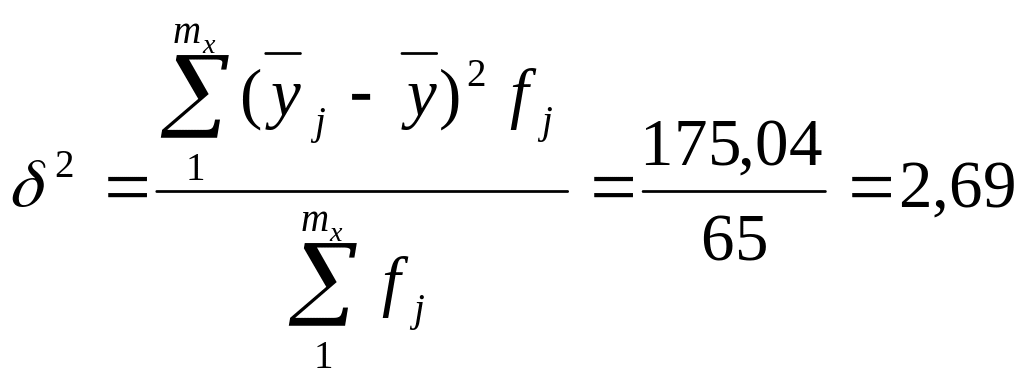
Кореляційне відношення:
,
тобто 61% варіації продуктивності праці на МТК пояснюється варіацією кількості корів.
Обчислення
та інтерпретація коефіцієнта детермінації
і кореляційного відношення
показують: ці характеристики щільності
зв’язку за змістом ідентичні, вони
характеризують внесок фактора х
у загальну варіацію результату у.