6.2.Регресійний аналіз.
Важливою характеристикою кореляційного аналізу є лінія регресії – емпірична в моделі аналітичного групування і теоретична в моделі регресійного аналізу.
Емпірична лінія регресії представлена груповими середніми результативної ознаки , кожна з яких належить до відповідного інтервалу значень групувального фактора (див. табл.6.2).
Теоретична
лінія регресії
описується певною функцією
,
яку називають рівнянням
регресії,
а Y
– теоретичним
рівнем результативності
ознаки. На відміну від емпіричної,
теоретична лінія регресії неперервна.
Залежно від характеру зв’язку статистика використовує різні за функціональним видом регресійні рівняння:
– лінійні
рівняння
–
,
коли із змінною х
ознака у
змінюється більш-менш рівномірно;
– нелінійні рівняння, коли зміна взаємопов’язаних ознак відбувається нерівномірно (з прискоренням, уповільненням або напрям зв’язку змінюється), зокрема:
степенева
гіперболічна
параболічна
В практиці частіше застосовуються лінійні рівняння або приведені до лінійного виду. У лінійному рівнянні параметр b – коефіцієнт регресії, який вказує, на скільки одиниць в середньому зміниться у зі зміною х на одиницю. Він має одиницю виміру результативної ознаки і розглядається як ефект впливу х на у.
Параметр a – вільний член рівняння регресії, тобто це значення У при х=0. Якщо х не набуває нульових значень, цей параметр має лише розрахункове значення.
Параметри рівняння регресії визначаються методом найменших квадратів, основна умова якого – мінімізація суми квадратів відхилень емпіричних значень y від теоретичних Y:
.
Математично доведено, що значення параметрів а та b, при яких мінімізується сума квадратів відхилень, визначається із системи нормальних рівнянь:
n∙a+b
a∙
b∙
Звідси:
,
Порядок обчислення параметрів лінійної регресії розглянемо на прикладі зв’язку між урожайністю зернових і кількістю внесених добрив (в центнерах діючої поживної речовини – д.р.). Взаємопов’язані ознаки та необхідні для розрахунку параметрів величини наведені в табл.6.2
Таблиця 6.2 – Матеріали до розрахунку параметрів лінійної регресії
Номер госпо- дарства |
Кількість внесених добрив,х ц.д.р |
Урожайність зернових,у ц/га |
х∙у |
х |
Y |
у - Y |
(у –Y) |
1 |
1,4 |
25 |
35,0 |
1,96 |
27,03 |
-2,03 |
4,12 |
2 |
2,0 |
33 |
66,0 |
4,00 |
33,29 |
-0,29 |
0,08 |
3 |
1,8 |
30 |
54,0 |
3,24 |
31,2 |
-1,2 |
1,44 |
4 |
1,3 |
28 |
36,4 |
1,69 |
26,0 |
2 |
4 |
5 |
1,2 |
26 |
31,2 |
1,44 |
24,95 |
1,05 |
1,10 |
6 |
1,1 |
23 |
25,3 |
1,21 |
23,91 |
-0,91 |
0,83 |
7 |
1,7 |
32 |
54,4 |
2,89 |
30,16 |
1,84 |
3,39 |
8 |
1,5 |
27 |
40,5 |
2,25 |
28,08 |
-1,08 |
1,17 |
9 |
1,6 |
29 |
46,4 |
2,56 |
29,12 |
-0,12 |
0,01 |
10 |
1,9 |
33 |
62,7 |
3,61 |
32,26 |
0,74 |
0,56 |
Разом |
15,5 |
286 |
451,9 |
24,85 |
286 |
х |
16,70 |
=15,5:10=1,55
=286:10=28,6
Користуючись цими величинами, визначаємо:
b=
ц/га
a= 28,6-10,424∙1,55=12,443
Отже, рівняння регресії має вигляд:
у= 12,443+10,424х
Тобто, кожний центнер внесених добрив (в перерахунку на діючу поживну речовину) дає приріст урожайності в середньому 10,424 ц/га. Якщо добрива не вносити (х=0), то урожайність зернових не перевищить 12,443 ц/га.
Рівняння регресії відбиває закон зв'язку між х і у не для окремих елементів сукупності, а для сукупності в цілому. Закон, який абстрагує вплив інших факторів, виходить з принципу «за інших однакових умов».
Вплив інших окрім х факторів зумовлює відхилення емпіричних значень у від теоретичних у той чи інший бік. Відхилення (у – Y) називають залишками і позначають символом e. Залишки, як правило, менші за відхилення від середньої, тобто:
(у – Y) ≤ (у - ).
У нашому прикладі
,
де
.
.
Відповідна загальна дисперсія врожайності:
у
-
.
Залишкова дисперсія:
.
Коефіцієнт регресії у невеликих за обсягом сукупностях схильний до випадкових коливань. Тому здійснюється перевірка його істотності за допомогою t – критерію (Стьюдента):
,
де b – коефіцієнт регресії;
–
стандартна
похибка.
Стандартна
похибка коефіцієнта регресії залежить
від варіації факторної ознаки
,
залишкової дисперсії
і числа ступенів свободи k = n – m, де m –
кількість параметрів рівняння регресії:
.
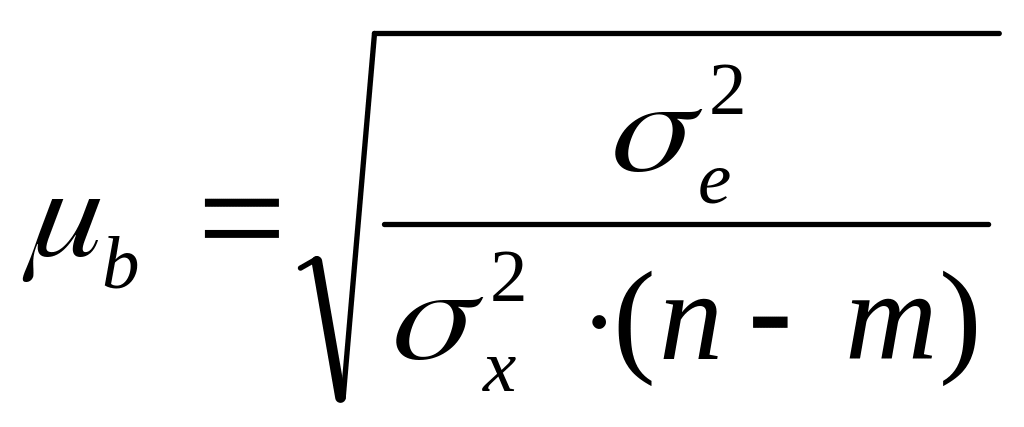Для лінійної функції m = 2. За даними табл.6.2 маємо:
.
Звідси:
(ц/га),
а
,
що
перевищує критичне значення t
– критерію
.
Гіпотеза про випадковий характер
коефіцієнта регресії відхиляється, а
отже, з імовірністю 0,95 вплив кількості
добрив на врожайність зернових
визначається істотним.
Для
коефіцієнта регресії визначаються
також довірчі межі:
.
В нашому прикладі довірчі межі коефіцієнта
регресії з імовірністю 0,95 (t
= 2,45) становлять 10,424±2,45∙1,59.
Важливою характеристикою регресійної моделі є відносний ефект впливу фактора х на результат у – коефіцієнт еластичності:
,
який показує, на скільки процентів у середньому змінюється результативна ознака у зі зміною фактора х на 1%. За даними нашого розрахунку:
,
тобто збільшення кількості внесених добрив на 1% приріст урожайності зернових у середньому складає 0,565%.
На підставі рівняння регресії визначаються теоретичні значення Y, тобто значення результативної ознаки за умови впливу лише фактора х при незмінному рівні інших факторів. Так, для
х = 1,5 ц теоретичний рівень урожайності становить 28,08 ц/га (Y = 12,443+10,424∙1,5), що дещо відхиляється від емпіричного значення (27 ц/га).