5.3. Статистичне вивчення варіації.

Варіація або коливання значень будь якої ознаки є властивістю статистичної сукупності, що зумовлено дією різних взаємопов’язаних причин.

Основні причини формують центр розподілу, другорядні – варіацію ознак. В одних сукупностях індивідуальні значення ознаки значно відхиляються від центру розподілу, в інших – тісно групуються навколо нього. Тому виникає потреба оцінити міру і ступінь варіації. Чим менша варіація, тим однорідніша сукупність, тим більш надійніші і типові характеристики центру розподілу – насамперед середні величини.

Для виміру і оцінки варіації використовують систему абсолютних і відносних характеристик, а саме: розмах варіації, середнє лінійне і середнє квадратичне відхилення, коефіцієнти варіації, дисперсію.

Розмах варіації – це різниця між найбільшим та найменшим значенням ознаки або як різниця між середніми значеннями останнього і першого інтервалів:

.

Надійність такої простої характеристики невисока, так як вона базується на двох крайніх значеннях, що можуть мати випадковий характер. Тому розмах варіації використовують для попередньої оцінки варіації. Інші показники варіації дають змогу усунути недолік розмаху варіації.

Середнє лінійне відхилення – це середня арифметична з абсолютних значень усіх відхилень індивідуальних значень ознаки від середньої:

а) просте ;

б) зважене .

При цьому не враховуються знаки відхилень, тобто їх спрямованість. Тому цей показник використовують рідко. Цей недолік усувається через дисперсію та середнє квадратичне відхилення.

Дисперсією називають середню арифметичну квадратів відхилень індивідуальних значень ознаки. В залежності від вихідних даних дисперсія може обчислюватися як проста або зважена:

а) проста ;

б) зважена .

Дисперсія – один з найбільш розповсюджених показників розміру варіації і використовується також для вимірювання зв’язків між досліджуваними факторами. Розклад дисперсії на складові дозволяє оцінити вплив різних факторів, що обумовлюють варіації.

Середнє квадратичне відхилення, як і дисперсія є узагальнюючим показником варіації і розраховується як квадратний корінь з дисперсії:

а) просте ;

б) зважене .

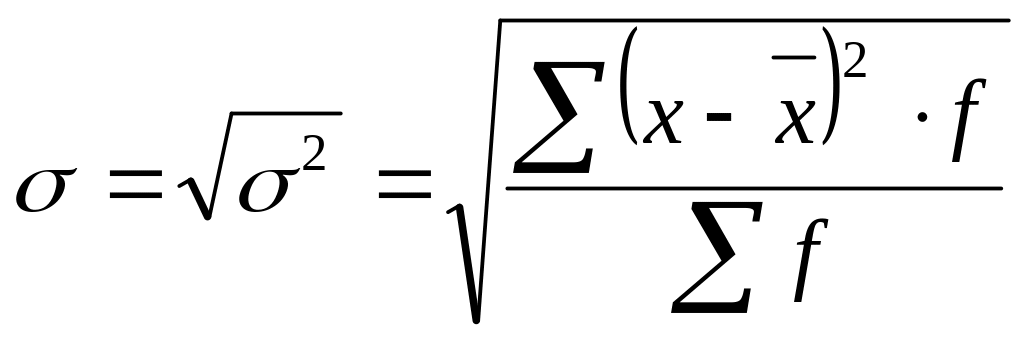Як і лінійне відхилення це відхилення показує на скільки в середньому відхиляються індивідуальні значення ознаки від їх середнього рівня. Воно виражається в тих же одиницях вимірювання, що і значення ознаки (грн., га) і цей показник також називають стандартним відхиленням.

Лінійне та квадратичне відхилення є ідентичними за змістом, проте завдяки їх математичним відхиленням . Статистичні показники варіації між собою пов’язані. При достатньо великому обсягу сукупності і розподілі близькому до нормального коливання значень ознаки незначні, тобто:

.

Розглянуті абсолютні показники варіації – розмах варіації, середнє лінійне і середнє квадратичне відхилення – іменовані величини, мають одиниці виміру варіюючої ознаки.

При порівнянні варіації різних ознак використовують відносні характеристики – коефіцієнти варіації, в т.ч. квадратичний коефіцієнт варіації – V і лінійний коефіцієнт варіації .

Коефіцієнт варіації – це відсоткове (%) відношення середнього квадратичного, лінійного відхилення до середньої арифметичної і розраховуються за допомогою таких формул:

лінійний ;

квадратичний .

Чим більший коефіцієнт варіації тим менш типова середня для даної сукупності. Встановлено, що сукупність кількісно однорідна, якщо коефіцієнт варіації не перевищує 33%.

Наведено приклад розрахунку показників варіації. Робітники одно з цехів підприємства у минулому році за стажем роботи розподіляться так:

Стаж роботи, років ( )	2	3	4	5	6	7
Кількість робітників ( )	6	16	20	10	6	2

Визначити середній стаж роботи, а також розрахувати основні показники варіації.

Середній стаж роботи визначаємо з допомогою формули середньої арифметичної зваженої тобто:

роки

Для розрахунку показників варіації використаємо табличний метод та алгоритм (табл. 5.7)

Таблиця 5.7 – Розрахунок показників варіації.

Вихідні дані		Розрахункові дані
Стаж роботи x	Кількість робітників f	( )
2	6	-2	12	4	24
3	16	-1	16	1	16
4	20	0	0	0	0
5	10	1	10	1	10
6	6	2	12	4	24
7	2	3	6	9	18
Всього	60	x	56	х	92

1. Розмах варіації

.

2 Середнє лінійне відхилення

.

3.Дисперсія

.

4.Середнє квадратичне відхилення

.

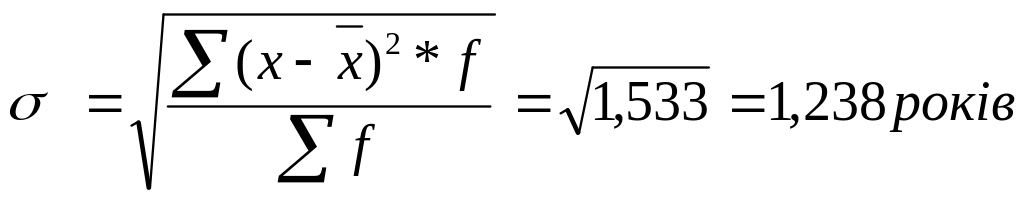5.Коефіцієнт варіації квадратичний

.

6. Коефіцієнт варіації лінійний

.

Таким чином встановлено, що досліджена сукупність є однорідною, а середня– типовою, так як коефіцієнт варіації квадратичний не перевищує 33 %