4.4. Середні величини

Середня величина в статистиці відображає характерний рівень ознаки, притаманної усім елементам сукупності. В середній величини нівелюються всі відмінності та особливості індивідуальних значень ознак.

Умовами застосування середніх величин є:

а) масовий характер даних сукупності;

б) якісна однорідність сукупності.

В статистиці використовується декілька видів середніх величин: середня арифметична, середня гармонійна, середня квадратична, середня геометрична, середня хронологічна та структурні середні – мода і медіана.

При дослідженні середніх використаємо такі позначення:

x або x_i – кожне індивідуальне значення ознаки;

f або f_i – частота повторень (вага) індивідуальної ознаки;

w = x·f – обсяг значень ознаки;

n – кількість одиниць досліджуваної ознаки;

– середнє значення досліджуваної ознаки.

Середня арифметична – це найпоширеніший вид середніх величин, який існує як проста середня арифметична та зважена середня арифметична.

Проста середня арифметична – обчислюється діленням загального обсягу значень ознаки на обсяг сукупності:

.

Наприклад, заробіток 5 робітників бригади за місяць був таким (грн.): 1980; 2150; 1540; 2360; 1620. Середня заробітна плата одного робітника складає:

.

Зважена середня арифметична використовується у тих випадках, коли значення ознаки подано у вигляді варіаційного ряду, в якому чисельність одиниць у варіантах неоднакова:

.

Наприклад, в результаті вибіркового обстеження 60 багатодітних сімей одержано такі такий варіаційний ряд (табл. 4.1).

Таблиця 4.1 – Розподіл багатодітних сімей за числом дітей

Число дітей у сім’ї , х	4	5	6	7	8	Всього
Кількість сімей, f	20	17	13	7	3	60
Розрахункові дані, х·f	80	75	78	49	24	306

Середня кількість дітей у сім'ї:

.

Середня гармонійна – це обернена до середньої арифметичної із обернених значень ознаки. Їх обчислюють при визначенні середніх витрат праці на одиницю продукції. При розрахунку середньої гармонічної зваженої відомими є загальний обсяг ознаки (w= x·f), індивідуальні значення ознаки (x), але невідома частота (f ).

Проста гармонійна .

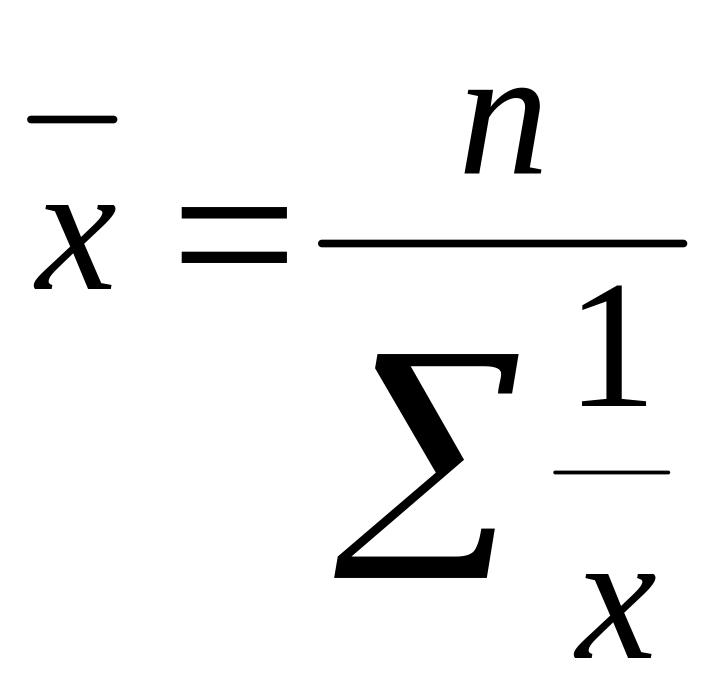Зважена гармонійна

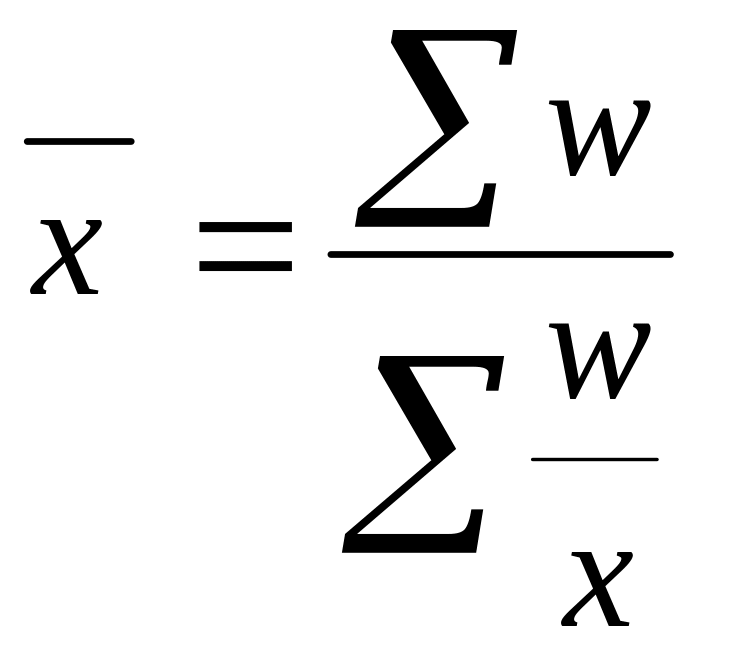
Її застосовують тоді, коли показник,що виступає статистичною вагою(f) відсутній і його слід додатково визначити на основі відомих варіацій (х) і добутку варіант на частоту (х f).

Розрахуємо середню урожайність озимої пшениці, виходячи з даних з даних табл. 4.2

Таблиця 4.2. Урожайність та валовий збір озимої пшениці одного з КСП

Бригади	Середня урожайність, ц/га	Валовий збір, ц
1	42,4	16125
2	38,0	7600
3	44,0	26840
Разом	x	50565

Саме посівна площа відіграє роль ваги. Цей показник відсутній, але його легко розрахувати, розділивши по кожній бригаді валовий збір на середню урожайність. В такому випадку середня урожайність складає:

.

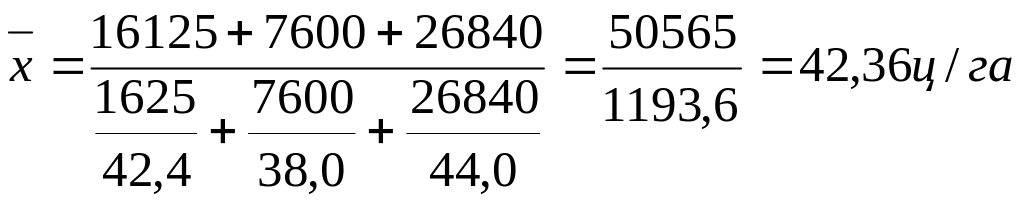Середня квадратична використовується для визначення показника варіації (коливання) ознаки – дисперсії та середнього квадратичного відхилення. Обчислюється на основі квадратів відхилень індивідуальних значень ознаки від їх середньої величини

проста ;

зважена ;

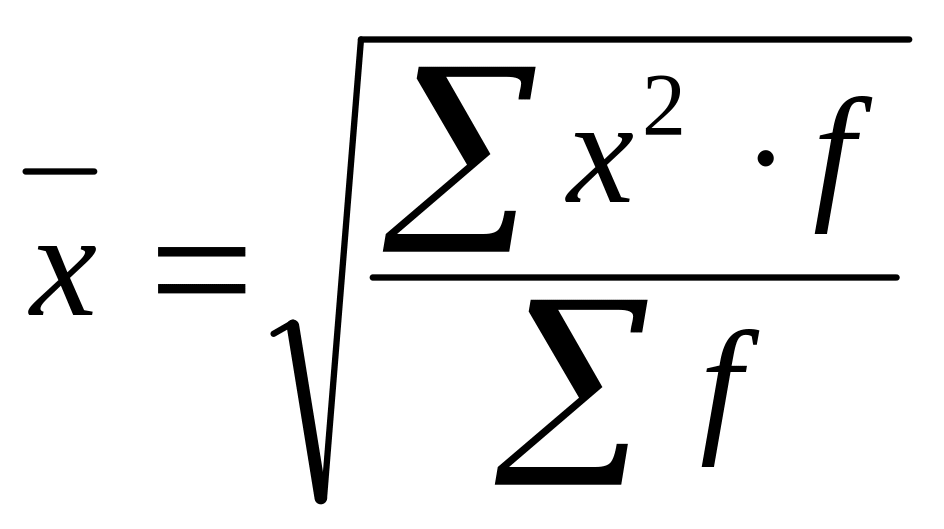Середня геометрична використовується для обчислення середніх темпів зростання в рядах динаміки:

,

де – темпи зростання;

m – кількість темпів зростання ( ).

Середню геометричну використовують, коли обсяг сукупності формується не сумою, а добутком індивідуальних значень ознаки. Застосування середньої геометричної розглянемо на прикладі розрахунку середньорічних темпів зростання ВВП в Україні. Обсяг ВВП (млрд. грн.): 2003-267,3; 2004-345,1; 2005 – 441,5; 2006 – 544,1; 2007 – 712,9.

.