Расчет сетевой модели

Метод сетевого планирования и управления предполагает широкое использование вычислительной техники для расчетов параметров сетевой модели, и только сетевые графики небольших размеров с успехом могут быть рассчитаны вручную.

Расчет сетевых графиков предполагает определение целого ряда показателей, которые должны дать представление о возможности перемещения работ по программе, об изменении их длительности и перераспределении ресурсов между работами комплекса.

Для всех событий в программе начиная с исходного определяется самая ранняя дата наступления – минимально необходимое время между наступлением исходного события и данного (здесь «K» – номер события). Это время обусловливается конфигурацией сетевой модели и связано со всеми событиями и работами, находящимися между исходным событием и данным.

Время характеризуется продолжительностью самого длинного пути от исходного события до анализируемого:

Т_Е(К) =мах t_1…K. (2.1)

Самая поздняя допустимая дата свершения события обозначает срок, за пределы которого недопустимо оттягивать свершение данного события, так как это вызовет увеличение времени выполнения всей программы. Время определяется разностью продолжительности критического пути и самого длинного пути от данного события (к) до конечного (n):

Т_L(К) =L _kp-мах t_K…n . (2.2)

Резерв времени для каждого события определяется по формуле

Р = Т_L(К) – Т_Е(К). (2.3)

При ручном расчете сетевого графика кружок, изображающий событие, делится на четыре сектора, в которые заносятся соответствующие показатели:

• верхний сектор Р – резерв события;

• нижний сектор – номер события;

• левый сектор Т_Е(К) – наиболее ранний срок свершения события;

• правый сектор Т_L(К) – наиболее поздний срок свершения события.

Так как любое событие в программе является начальным для одних работ и конечным для других, рассчитываются и допустимые сроки выполнения и резервы времени по работам.

Раннее начало работы

. (2.4)

Раннее окончание работы

. (2.5)

Позднее начало работы

. (2.6)

Позднее окончание работы

. (2.7)

Полный резерв времени – это количество времени, на которое можно перенести начало работы или увеличить ее продолжительность без изменения общего срока выполнения всей программы:

. (2.8)

Частичный резерв времени показывает, сколько времени имеется в запасе при выполнении работы i-j , чтобы не сорвать наиболее ранние сроки начала последующих работ.

. (2.9)

Определение резервов времени – важный этап расчета сетевого графика, так как эти резервы характеризуют возможность перераспределения материальных и трудовых ресурсов между работами внутри комплекса с целью сокращения общего времени выполнения всего объема работ.

Анализ и оптимизация сетевого графика

Анализ сетевых графиков осуществляется для последующей оптимизации по времени и трудовым ресурсам.

Корректировка сетевых графиков по времени

Процесс корректировки сетевого графика по времени предусматривает достижение директивного срока без учета ограничений по трудовым ресурсам.

Расчетный критический путь первоначального варианта сетевого графика может оказаться равным, меньшим или большим заданного директивного срока .

В первом случае, когда , нет необходимости выполнять корректи­рование сетевого графика по времени.

Во втором случае, когда , возникает дополнительный резерв времени , который может быть использован для увеличения продолжительности отдельных критических работ при последующей оптимизации в случае необходимости.

В третьем случае, когда , сетевой график следует пересмотреть с целью его уплотнения. Главная задача, решаемая при этом, состоит в ускорении тех работ, из которых в каждом случае складывается критический путь.

Уплотнение сетевого графика производится обычно несколько раз методом последовательных приближений, т.е. многократным сжатием очередного критического пути до получения удовлетворительного результата.

Существует несколько методов приведения сетевого графика в соответствие с директивными сроками.

1. Изменение временных оценок путем замены нормальной продолжительности выполнения работ сокращенной, т.е. переход на ускоренный режим выполнения работы с добавлением ресурсов (механизмов или исполнителей).

Общий срок выполнения комплекса операций следует сокращать, прежде все­го, за счет изменения продолжительности критических работ. В этом случае сетевой график не вычерчивается заново, а меняются лишь временные оценки критических работ. При этом рекомендуется также уменьшать продолжительность работ, лежащих на подкритических путях, так как последние могут стать новыми критическими путями.

Уменьшение временных оценок по критическим работам обеспечивается за счет переброски соответствующих ресурсов с работ, обладающих значительными резервами времени.

Если внутренних ресурсов недостаточно, следует рассматривать возмож­ность дополнительного привлечения исполнителей и оборудования.

2. Изменение последовательности выполнения работ вследствие пересмотра технологии выполнения всего комплекса. Такой пересмотр возможен в том случае, если отдельные работы могут выполняться различными методами. Сокращение сроков может быть обеспечено также и за счет того, что ряд работ, которые ранее выполнялись последовательно, при измененной технологии могут выполняться параллельно.

3. Расчленение работ и их совмещение во времени. Параллельное выпол­нение работ достигается расчленением лежащих на критическом пути работ большой продолжительности, что дает возможность начать последующие работы еще до полного окончания предшествующих.

В ходе корректировки сетевого графика по времени надлежит постоянно проверять длительность остальных путей и сравнивать их между собой во избежание возникновения новых критических путей.

Если после всех принятых мер по сокращению продолжительности выполнения комплекса операции директивный срок не достигнут, следует рассмотреть возможность изменения этого срока.

Оптимизация сетевого графика по трудовым ресурсам

После построения, расчета сетевого графика и его корректировки по времени следует выполнить оптимизацию сетевого графика по трудовым ресурсам, т.е. по количеству занятых исполнителей. Это производится для правильного распределения персонала и обеспечения его постоянной загрузки в течение всего срока выполнения планируемого комплекса работ.

Задача выравнивания ресурсов становится практически выполнимой при следующих условиях:

• плотность используемого на работе ресурса остается неизменной на протяжении всей работы;

• начало или окончание каждой работы может осуществляться только на границе двух единиц времени, принятых для данного сетевого графика, но не в пределах этих единиц.

При соблюдении указанных условий график занятости исполнителей в функции времени N = f(t) будет всегда иметь ступенчатый характер с минимальной длиной ступеньки, равной единице времени (час, смена, сутки и т.д.). Критерием оптимальности в задаче выравнивания количества исполнителей является равномерность их занятости в течение всего срока выполнения комплекса работ. Математически этот критерий характеризуется среднеквадратичным отклонением количества ежедневно занятых исполнителей от среднего их числа за время работы. Целью оптимизации является минимизация этого отклонения.

Далее рассматривается вывод математического критерия оптимизации сетевого графика по трудовым ресурсам.

				L
	К	nKL
	i Ni	i+1 Ni+1	............	j Nj	j+1 Nj+1	дни чел.

Рис. 2.1. Фрагмент линейной диаграммы

Допустим, имеется некоторая работа k-1 продолжительностью m дней (рис. 2.1). Условимся отмечать первый день выполнения работы номером i, а последний – номером j. В этом случае в продолжительность m входят дни под номерами i, (i+1), (i+2), ... , j. Количество исполнителей, занятых на данной работе k-1, обозначим n_KL. Суммарное количество исполнителей, занятых на всех работах оптимизируемого графика, обозначим символом N. В те дни, когда выполняется исследуемая работа k-1, N приобретает значения N_i, N_(i+1) и т.д. Чтобы установить, будет ли увеличиваться или уменьшаться минимизируемая функция при перемещении работы на один день вправо, т.е. когда ее первым днем выполнения будет i+1 день вместо дня i, а последним будет день j+1, необходимо вычислить изменение среднеквадратичного отклонения :

. (2.10)

Среднеквадратичное отклонение до перемещения работы – ₁, после перемещения – ₂:

(2.11)

Тогда

=2n_kl N_j+1-(N_i-n_kl). (2.12)

Так как , то на знак величины влияет лишь значение показателя .

При среднеквадратичное отклонение уменьшится, следовательно, сдвиг работы на один день вправо целесообразен (если это разрешает резерв времени этой работы).

При среднеквадратичное отклонение не изменится. Этот случай является неопределенным, так как сдвиг работ не сокращает неравномерности потребляемого ресурса, но ведет к его уплотнению.

При среднеквадратичное отклонение увеличивается, следовательно, сдвиг работы на один день вправо нецелесообразен.

В случае, когда работа сдвигается на один день вправо, необходимо откорректировать и суммарную численность исполнителей в день номер i ( ), и день номер j+1 ( ). После этого исследуется целесообразность последующего перемещения работы k-1 на один день вправо тем же способом.

В случае, когда сдвиг работы вправо нецелесообразен ( ), необходимо проанализировать целесообразность сдвига работы сразу на два, затем на три и больше дней, вплоть до исчерпания резерва времени этой работы. Такой сдвиг может оказаться целесообразным, если на пути передвижения работы по оси времени вправо окажется, что после периода времени с максимальной численностью исполнителей существует период с небольшой численностью (впадина), в пределах которой можно разместить перемещаемую работу. Поэтому, зафиксировав величину при ее положительном значении , определяют для следующей пары дней.

Выполняют перемещение еще на один день вправо .

Затем суммируют эти величины .

В том случае, если , что возможно при условии и , работу целесообразно переместить сразу на два дня вправо. После этого, скорректировав суммарную численность исполнителей по дням, производят анализ целесообразности дальнейшего перемещения работы таким образом, как будто бы предшествующего передвижения не было.

Если же окажется, что , исследуют целесообразность перемещения работы сразу на три дня:

. (2.13)

Такие исследования выполняются и далее вплоть до полного исчерпания резерва времени работы.

Для подсчета суммарной ежедневной занятости исполнителей и анализа целесообразности перемещения работ по оси времени строится упрощенная масштабная линейная диаграмма сетевого графика (рис. 2.2). Следует иметь в виду, что выполнив первый шаг оптимизации и исследовав целесообразность перемещения всех работ с резервами времени (и их соответствующего сдвига), нужно произвести аналогично второй, а может быть, и третий шаг оптимизации, что улучшит достигнутое на предыдущем шаге качество выравнивания численности исполнителей в течение всего срока выполнения комплекса работ.

Ниже рассматривается применение метода и алгоритма выравнивания численности исполнителей на примере небольшого абстрактного сетевого графика (рис. 2.3). В графике над каждой работой указана ее продолжительность в днях, под работой – количество исполнителей, в квадратных скобках – полный и частичный резервы времени.

Критический путь проходит через события 1-3-4-6-8, L_kp = 15. Выравнивание (оптимизация) численности выполняют в следующей последовательности.

1. Строят линейную диаграмму сетевого графика. Горизонтальную ось графика делят на 15 равных отрезков (по количеству дней выполнения программы), а вертикальную – на количество равных отрезков по числу работ в сетевом графике (рис. 2.2).

2. Работы в линейной диаграмме размещают снизу вверх, руководствуясь следующими правилами:

а) размещают все работы, отходящие от первого события, затем от второго и т.д.;

б) размещают работы, отходящие от одного события, в порядке возрастания полного резерва времени таким образом, чтобы работы с меньшим резервом располагались ниже, чем работы с большим резервом;

в) работы изображают линиями в масштабе времени в положении, соответствующем их наиболее раннему началу, и обозначают их числами, соответствующими их шифру;

г) над каждой работой указывают ее ресурс – количество исполнителей.

3. Подсчитывают ежедневную суммарную потребность ресурса по дням и записывают ее в горизонтальной строке под линейной диаграммой (рис. 2.2).

4. Строят ступенчатую кривую изменения количества исполнителей N = f(t) по дням в координатах N, t (тонкая линия на рис. 2.4).

Выровнять тонкую линию N = f(t) можно только путем перемещения части работ в пределах их резерва времени вправо.

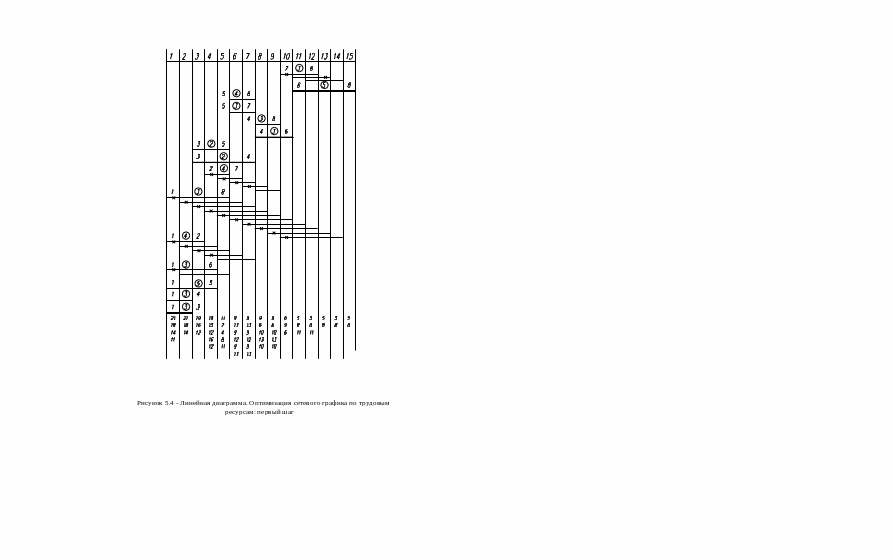
Рис. 2.2. Линейная диаграмма.

Оптимизация сетевого графика

по трудовым ресурсам – первый шаг

Целесообразность такого перемещения работы устанавливается вычислением показателя . При < 0 смещение работы вправо целесообразно. На первом шаге оптимизации таким образом просматриваются все работы сверху вниз.

Рис. 2.3. Сетевой график до оптимизации

Рис. 2.4. График использования трудовых ресурсов

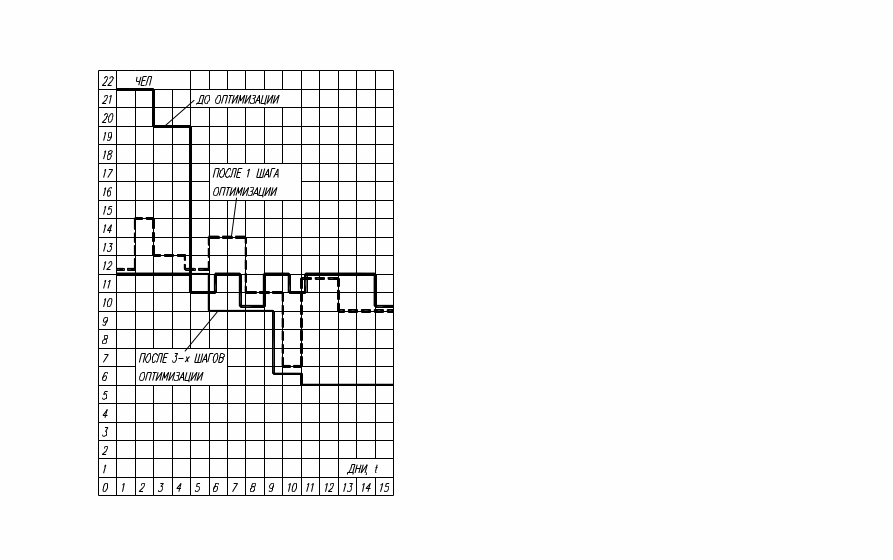
Рис. 2.5. Оптимизация сетевого графика по трудовым ресурсам:

в торой и третий шаги

Например, на рис. 2.2 резерв работы 7-8 составляет 5 дней. Работа может быть перемещена до конца линейной диаграммы, т.е. до совмещения цифры 8 на конце работы 7-8 с цифрой 8 на конце последней работы критического пути 6-8. Проверяем целесообразность перемещения этой работы на один день вправо. Считая i = 8, j = 10, j+1 = 11, вычисляем = 5 - (9 -3) = = -1. Следовательно, сдвиг работы 7-8 на один день вправо целесообразен. Выполняем этот сдвиг и корректируем суммарные ресурсы (количество исполнителей) в дни i и j+1 = 9 - 3 = 6; = 5 + 3 = 8. Новые значения ресурсов вписываем под линейной диаграммой в соответствующих 8-му и 11-му столбцах и используем их в дальнейших расчетах. Затем проверяем целесообразность перемещения этой же работы 7-8 на один день вправо (так как резерв времени не исчерпан).

= 5 - (9 - 3) = -1.

Осуществляем сдвиг, корректируем и записываем новые значения суммарного ресурса в дни 9 и 12:

=9-3=6, =5+3 -8.

Проверяем целесообразность сдвига этой работы еще на один день вправо:

= 5 - (6 - 3) = +2, т.е. такой сдвиг нецелесообразен.

Проверяем возможность сдвига на два дня: =5-(8-3)= О, = = 2 + 0 - 2, т.е. сдвиг на два дня тоже не целесообразен. Проверяем возможность сдвига на три дня: = 5 - (8 - 3) = О, = 2 + 0 +0 = 2, т.е. сдвиг на три дня также нецелесообразен. Так как целесообразность перемещения работы 7-8 проанализирована в пределах всего резерва времени, следует перейти к следующей работе 5-8, расположенной ниже, пропуская при этом критическую работу 6-8, и проанализировать целесообразность ее перемещения вправо в пределах ее резерва времени. Таким образом, анализируется возможность перемещения всех работ вплоть до работы 2-4. Этим заканчивается первый шаг оптимизации по ресурсам.

После этого аналогично выполняется второй шаг (а при необходимости – и следующие шаги) оптимизации. Весь последующий анализ выполняется на той же линейной диаграмме, однако для большей наглядности он показан на новой диаграмме (рис. 2.5), исходными данными для построения которой служат результаты сдвигов работ, выполненные на первом шаге (см. рис. 2.2). В данном случае все возможности улучшения использования ресурсов исчерпаны вторым шагом оптимизации.

Дальнейшее выравнивание ресурсов по дням можно осуществить только путем изменения режима выполнения отдельных работ – переводом в замедленный режим в пределах их резервов времени с соответствующим уменьшением количества исполнителей.

Просматривая поочередно величины ежедневной суммарной потребности исполнителей, отмечаем дни, в которые эти значения максимальны.

В нашем примере N_мaх (12 чел.) на 6-й и 7-й день. Просмотром по вертикали устанавливаем перечень работ, выполняемых в эти дни, затем с учетом технологической возможности переводим эти работы поочередно в замедленный режим в пределах их резервов времени, в результате чего добиваемся дальнейшего сглаживания графика занятости. В нашем примере на 6-й и 7-й день намечено выполнение работ 1-6, 1-2, 3-4, 5-7. Из этих работ резервы времени имеют 1-6 и 5-7. Переводим в замедленный режим работу 1-6, уменьшив количество исполнителей с трех человек до двух. При этом продолжительность работы возрастает с четырех дней до шести, а трудоемкость выполнения остается прежней (4*3 = 6*2 = 12 человеко-дней). Начало работы 1-6 целесообразно сместить на два дня влево, так как на 3-й и 4-й день суммарная потребность в исполнителях составляет только 9 человек. Изменив длину работы, время ее начала и количество исполнителей на линейной диаграмме (см. рис. 2.5), корректируем потребность в исполнителях на 3-й, 4-й, 5-й, 6-й, 7-й и 8-й дни. На этом работа по оптимизации ресурсов может быть прекращена, так как полученный график N = f(t) достаточно равномерен. Ступенчатые кривые на рис. 2.4 показывают выравнивание в дневной потребности исполнителей работ после первого и двух последующих шагов оптимизации.

На заключительном этапе оптимизации кроме перевода работ в замедлен­ный режим выполнения может быть применен способ установления перерывов в производстве некоторых работ на те дни, когда слишком велика суммарная потребность исполнителей. При этом следует убедиться в технологической возможности перерывов. Однако нежелательно создавать длительные разрывы в работах, временно прерванная работа должна быть завершена при первой же возможности.

После выравнивания ресурса надо внести в сетевой график коррективы, отражающие сдвиги работ, изменения режима выполнения части работ и допущенные перерывы в их производстве. В результате в нем могут появиться организаци­онные ожидания, признаком которых будет нулевое количество исполнителей. График приобретает вид, изображенный на рис. 2.6. Такой график может быть календаризирован и принят к исполнению в качестве оперативного плана работ.

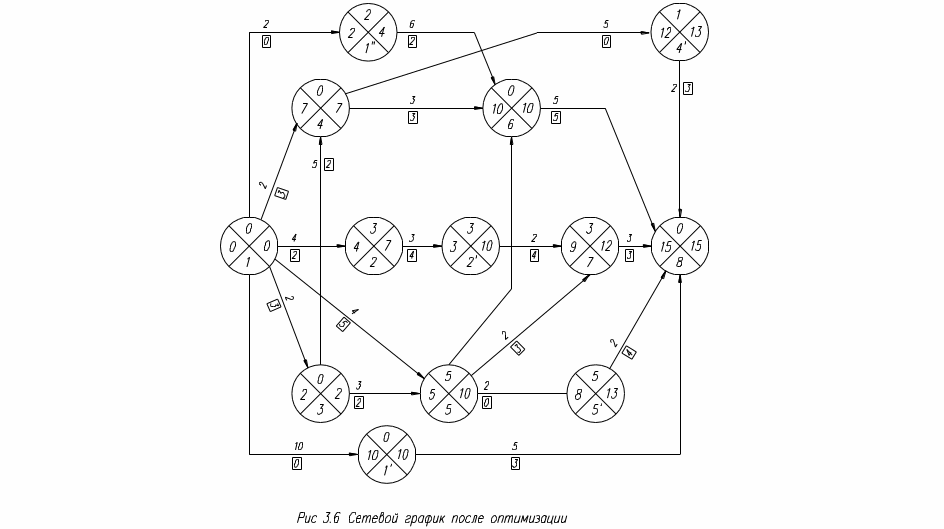
Рис. 2.6. Сетевой график после оптимизации

При выполнении курсовой работы в качестве исходных данных выступает некоторый известный студенту комплекс работ – технологический процесс, порядок и взаимосвязь работ в котором может быть определена. Количество работ в программе должно составлять не менее 20. Для всех работ экспертным путем нужно определить продолжительность выполнения и количество исполнителей. Затем необходимо представить этот комплекс работ в виде сетевого графика, рассчитать все указанные выше параметры и, при необходимости и возможности, оптимизировать его.