2.3. Оптимизация производственной программы на основе графической задачи и симплекс-метода

2.3.1. Назначение и цель работы

При выполнении настоящей курсовой работы необходимо оптимизировать производственную программу фирмы на основе анализа некоторых хозяйственных показателей.

Для оптимизации программы рекомендуется использовать модели линейного программирования  графический метод решения задачи и симплекс-метод.

2.3.2. Постановка задачи

Некоторая фирма имеет возможность изготавливать определенные виды продукции (табл. 2.14). Известны ресурсы, которые расходуются на изготовление каждого вида продукции, и при этом также задан расход ресурса каждого типа на единицу продукции (табл. 2.12).

Известен запас ресурсов каждого типа в фирме по вариантам задания (табл. 2.15). Задан размер прибыли (в д.е.), получаемой от реализации единицы продукции каждого вида (табл. 2.13). Необходимо составить оптимальный план выпуска продукции, т.е. определить количество единиц товаров каждого вида, выпуск и реализация которых обеспечат фирме получение максимальной прибыли.

В настоящих методических указаниях далее приведены исходные данные для решения поставленной задачи.

При решении поставленной задачи необходимо использовать метод графического решения и (или) симплекс-метод, и объяснить, почему можно или нельзя использовать ту или иную модель решения задачи.

2.3.3. Графическое решение задачи

Графически (геометрически) задача решается очень просто и наглядно, но применить данный способ можно лишь в том случае, если задача содержит две неизвестные величины. Например, фирма выпускает два вида продукции  «m» и «n», известны ресурсы («c», «d», «k», «e») и их расход на единицу продукции, а также запас этих ресурсов. Задана и прибыль от реализации единицы продукции каждого вида.

Все эти данные приведены в табл. 2.7. Для решения задачи следует обозначить количественный выпуск изделий «m» – X₁, а изделий «n» – Х₂. Теперь можно представить условия (ограничения) задачи в виде неравенств (2.27)  (2.31), а целевую функцию – формулой (2.32).

Таблица 2.7

Условие задачи

Типы используемых ресурсов	Расход ресурсов на единицу продукции (единиц)		Наличие ресурсов (единиц)
	m	n
c	2	5	300
d	3	4	360
k	-	3	150
e	4	5	600
Прибыль от реализации единицы продукции (д.е.)	3	10

Затем в системе координат Х₁-Х₂ необходимо построить области, соответствующие ограничениям по ресурсам (2.27)  (2.31).

С учетом условия (2.27) построение следует производить в I квадранте координатной сетки (рис. 2.8).

В табл. 2.8 приведены значения координат Х₁ и Х₂ для построения ограничивающих прямых для областей значений неизвестных (2.28) – (2.31) по двум точкам.

Таблица 2.8

Расчет координат ограничивающих прямых

№ пря-мой	Уравнение прямой	Координаты 1-й точки		Координаты 2-й точки
		Х1	Х2	Х1	Х2
1	2Х1+5Х2=300	0	60	150	0
2	3Х1+4Х2=360	0	90	120	0
3	3Х2=150	-	50
4	4Х1+5Х2=600	0	120	150	0

Из всех возможных точек области допустимых решений oabcd нас интересуют лишь те (или та), которые соответствуют плану выпуска продукции, обеспечивающему максимальную прибыль.

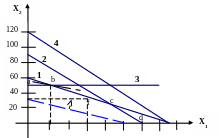
0

20 40 60 80 100 120 140 160

Рис. 2.8. Решение задачи

Для определения оптимального плана на том же рис. 2.8 надо построить прямую прибыли (целевой функции F), присвоив любое численное значение F, например, 300.

Теперь имеем:

F=3Х₁+10Х₂=300. (2.33)

Из (2.33) получим координаты двух точек для построения:

1-я: Х₁=0; Х₂=30, (2.34)

2-я: Х₁=100; Х₂=0.

Ясно, что чем больше значение прибыли F, тем дальше от начала координат перемещается прямая F параллельно себе самой. Поэтому прямую F на рис. 2.8 перемещаем параллельно себе самой от начала координат до тех пор, пока эта прямая будет иметь хотя бы одну общую точку с областью oabcd.

Такой точкой является точка «b». Координаты этой точки и соответствуют оптимальному плану: Х1=25; Х2=50. При этом прибыль фирмы F=3*25+10*50=575 д.е.