1.
Бросают 2 монеты. События А – «герб
на первой монете» и В – «цифра на
второй монете» являются
1)
совместными 2) несовместными
3) зависимыми 4) достоверными
2.
Для сигнализации об аварии
установлены 2, независимо работающих
сигнализатора. Вероятность того,
что при аварии сработает первый
сигнализатор, равна 0,9 , второй –
0,8.
Найти вероятность того, что при
аварии сработает только один
сигнализатор.
1)
0,44
2) 1,7
3) 0,56
4) 0,26
3.
СВ X
принимает два значения 4 и 5, а ее
матожидание равно 4,6. Найти D(X).
1)
0,15
2)
– 0,81
3)
0,24
4)
0,4
4.
СВ X
распределена по нормальному закону.
Статистическое распределение
выборки представлено в таблице
x
|
3
|
5
|
n
|
3
|
7
|
Найти
с надежностью 0,99 доверительный
интервал для генерального среднего.
1)
(0; 4,44) 2) (3,44; 5,36) 3) (2,01;
3,07) 4) (4,02; 4,58)
5.
Случайная величина X
задана функцией распределения
F(x)
=

Найти
P(1<
x
< 2).
1/16
2) 4
3) 1/8
4) 3/16
Вариант
10
1.
Среди 6 компьютеров, имеющихся в
классе, лишь 4 новых, остальные –
б/у. Наугад взяли один компьютер.
Найти вероятность того, что он –
новый.
1)
1/6
2) 1/3
3) 2/3
4) 1/4
2.
Вероятность попадания стрелком в
десятку – 0,4; а в девятку – 0,6.
Определить вероятность того, что
при 2-х выстрелах стрелок наберет
более 18 очков.
1)
0,16 2) 0,38 3) 0,4
4) 0,64
3.
Для рекламы фирма вкладывает в
каждую десятую единицу продукции
приз в 2000 руб. Пусть СВ X
– размер выигрыша при двух сделанных
покупках. Найти матожидание СВ X.
1)
400
2) 2000
3) 100
4)
200
4.
Как вычисляется дисперсия
результатам выборки объема n:
1)
 2)
2)
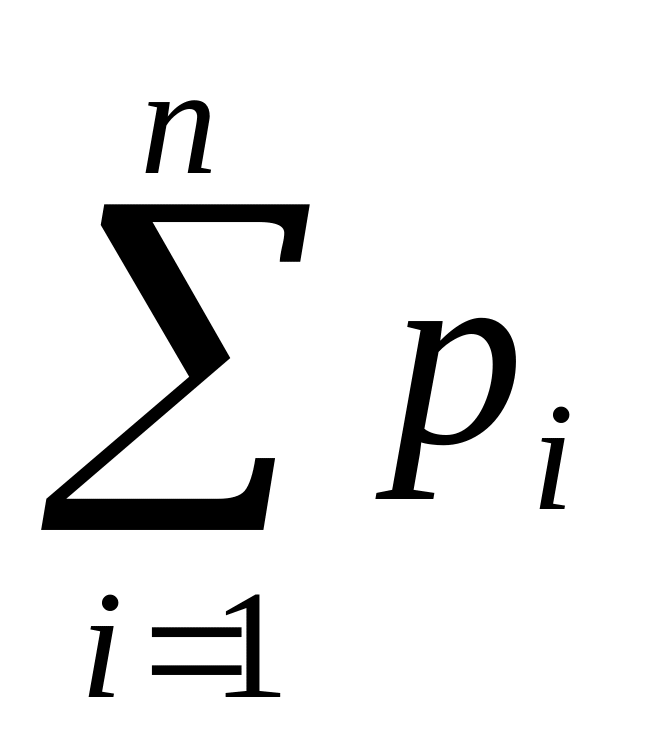 3)
3)
 4)
4)

5.
Из большого количества деталей
отобрано 100, распределение которых
по размеру задано в таблице.
Размер
детали
|
8
–8,2
|
8,2
– 8,4
|
Количество
|
20
|
80
|
Найти
95%-ный доверительный интервал для
матожидания.
(8,244;
8,276) 2) (4,234; 5,256) 3) (6,352;
10,327) 4) (1,535; 4,328)
Вариант
11
В
ящике имеется 5 пар зимней и 10 пар
летней обуви. Наудачу извлекается
одна пара. Найти вероятность того,
что это будет пара летней обуви.
1)
1
2) 1/2
3) 2/3
4) 1/3
2.
Исследователь разыскивает нужные
ему сведения в 3-х справочниках.
Вероятности того, что сведения
находятся в первом, во втором и
третьем справочниках равны
соответственно 0,7 , 0,6 , 0,9. Найти
вероятность того, что требуемые
сведения содержатся хотя бы в одном
справочнике. 1) 0,638 2)
0,135 3) 0,988 4) 0,288
3. Дискретная случайная величина
Х задана рядом распределения

|
− 2
|
0
|
2
|
3
|

|
0,2
|
0,2
|
0,2
|
0,4
|
Найти
P(0
< X
< 5).
1) 0,4 2) 0,6
3) 0,2 4) 0,8
4.
Найти несмещенную оценку матожидания
СВ
X
на основании данного распределения
выборки:
1)
19/3 2) 7 3) 22/3
4) 41/3
5.
Завод отправил в торговую сеть 500
изделий. Вероятность повреждения
в пути равна 0,002. Найти вероятность
того, что при транспортировке будет
повреждено более трех изделий.
1)
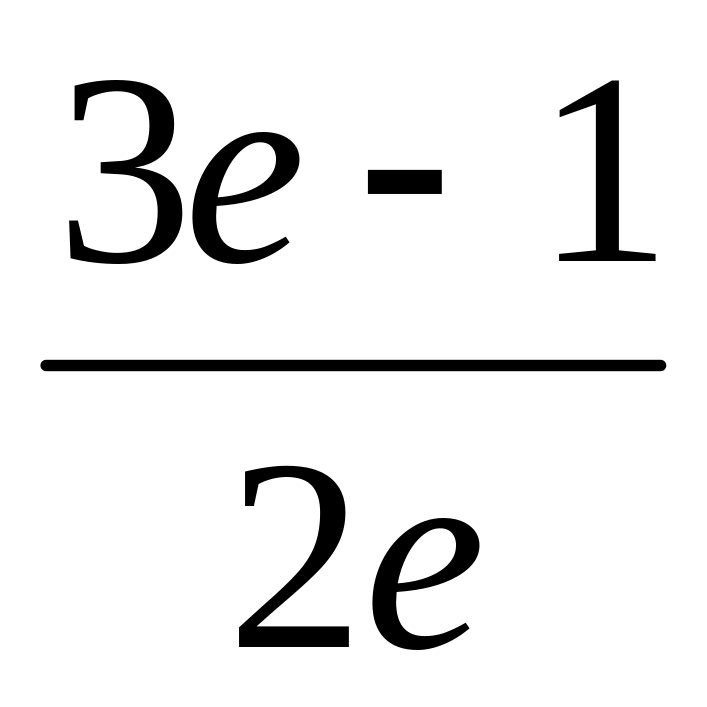 2)
2)
 3)
3)
 4)
4)

Вариант
12
1.
На отрезке AB
произвольно нанесены 2 точки.
Какова вероятность того, что наудачу
выбранный отрезок из числа всех
образовавшихся одним из своих
концов имеет точку A?
1)
1/2
2) 1/3
3) 1/4
4) 1/5
2.
В ящике имеется 15 пар обуви, из
которых 5 пар зимней. Наудачу
извлекается 4 пары. Найти вероятность
того, что три из них будут парами
летней обуви.
1)
1/3 2) 40/91 3) 24/35
4) 52/61
3.
Задан закон распределения случайной
величины X:
Х
|
1
|
3
|
5
|
7
|
9
|
p
|
1/15
|
2/15
|
3/15
|
4/15
|
|
Тогда
значение M(X)
равно
1) 19/3 2) 20/3 3) 22/3
4) 14/3
4.
Найти несмещенную оценку дисперсии
СВ
X
на основании данного распределения
выборки:
1)
6,08 2) ‒ 3,24 3)
3,37 4) 2,06
5.
Курс доллара повышается в течение
квартала с вероятностью 0,9 и
понижается с вероятностью 0,1. При
повышении курса доллара фирма
рассчитывает получить прибыль с
вероятностью 0,85, а при понижении –
с вероятностью 0,5. Найти вероятность
того, что фирма получит прибыль.
1) 0,912 2) 0,815 3) 0,515
4) 0,85
Вариант
13
Из
колоды карт (их 36) наугад вынимают
одну карту. Найти вероятность того,
что эта карта будет бубновой масти.
1)
1/3
2) 1
3) 1/4
4) 1/6
В
ящике 4 апельсина и 5 лимонов. Наудачу
достают 3 штуки. Какова вероятность
того, что среди отобранных будет
хотя бы один лимон?
1)
19/21 2) 4/21 3) 1/21
4) 20/21
3.
Случайная величина X
имеет закон распределения,
определяемый таблицей
Х
|
0,1
|
0,2
|
0,3
|
p
|
0,2
|
0,4
|
0,4
|
Найти
дисперсию случайной величины Y
= 5X
– 1.
1)
0,035 2) 0,028 3) ‒
1,3856 4) 0,1
4.
Найти минимальный объем выборки,
при котором с надежностью 0,95
точность
оценки
матожидания нормально распределенной
генеральной совокупности по
выборочной
средней равна 0,2. Известно, что
среднее квадратичное
отклонение
генеральной совокупности равно
1,5.
1)
154 2) 183 3) 100
4) 215
5.
Вероятность малому предприятию
стать банкротом за время t
равна 0,2. Найти вероятность того,
что из четырех малых предприятий
за время t
сохранятся хотя бы 2.
1)
0,9728 2) 0,5316 3)
0,2817 4) 0,6319
Вариант
14
Студент
знает ответы на 10 из 15 вопросов
программы. Найти вероятность того,
что он не знает ответ на предложенный
ему экзаменатором вопрос.
1
2) 1/3
3) 1/10
4) 2/3
В
урне находится 12 белых и 8 черных
шаров. Найти вероятность того, что
среди наугад вынутых пяти шаров
три будут черными.
1)
14/225 2) 18/101 3) 1
4) 77/323
3. Дискретная случайная величина
Х задана рядом распределения
|
− 2
|
0
|
2
|
3
|
|
0,2
|
0,2
|
0,2
|
0,4
|
Найти
P(X
< 2).
1)
0,2 2) 0,6 3) 0,4
4) 0
4.
Приведена статистика по годовым
темпам (%) инфляции в стране за
последние 5 лет:
2,8;
3,2; 5,1; 1,8; − 0,9. Найти оценку среднего
квадратичного отклонения.
1)
‒ 1,15 2) 2,12 3)
8,76 4) 3,54
5.
Среди молодых людей, прибывающих
в военкомат, 40 % признаются негодными
к воинской службе. Какова вероятность
того, что из 4-х вызванных наудачу
призывников только двое будут
признаны годными?
1)
0,25 2) 0,4 3) 0,2318
4) 0,3456
Вариант
15
В
денежно-вещевой лотерее на каждые
10000 билетов разыгрывается 150 вещевых
и 50 денежных выигрышей. Чему равна
вероятность выигрыша, безразлично
денежного или вещевого, для владельца
одного лотерейного билета?
1/150
2) 1/200
3) 1/50
4) 0
Из
8 акционерных обществ 4 являются
банкротами. Гражданин приобрел по
одной акции трех АО. Какова
вероятность того, что среди купленных
акций две окажутся акциями банкротов?
1)
4/7 2) 1/7 3) 2/7
4) 3/7
3.
По ряду распределения СВ X
найти М(Х).
1)
6 2) ‒ 2 3) 4,2
4) 3,6
4.
Из большого количества деталей
отобрано 4, распределение которых
по размеру следующее: 8, 6, 9, 5. Найти
несмещенную выборочную оценку
дисперсии.
1)
5,3 2) 3,3 3) ‒ 1,2
4) 7,3
5.
В партии изделий, в которой 80 %
стандартных, товаровед отбирает
3 изделия. Какова вероятность того,
что среди отобранных будет хотя бы
два стандартных.
1)
0,992 2) 0,334 3) 0,8
4) 0,2108
Вариант
16
В
магазин поступило 30 холодильников,
пять из которых имеют заводской
дефект. Случайным образом выбирается
один холодильник. Какова вероятность
того, что он будет без дефекта?
1)
1/6
2) 5/6
3) 5/18
4) 1
2.
Из колоды карт (36 листов) вынимаются
2 карты. Найти вероятность того,
что
эти
карты будут разных мастей.
1)
1/35 2) 13/35 3) 27/35
4) 18/35
3.
Задан закон распределения случайной
величины X:
Х
|
1
|
3
|
5
|
7
|
9
|
p
|
1/15
|
2/15
|
3/15
|
4/15
|
1/3
|
Тогда
вероятность Р(3 ≤ X
< 7) равна
1)
1/2 2) 1/5 3) 2/3
4) 1/3
4.
Из большого количества деталей
отобрано 4, распределение которых
по размеру следующее: 8, 7, 9, 6. Найти
несмещенную выборочную оценку
среднего квадратичного отклонения.
1)
1,29 2) 2,13 3) 0,16
4) ‒ 1,25
5.
Ученик пришел на экзамен, зная 25
билетов из 30-ти. Перед ним был взят
только 1 билет. Какова вероятность
того, что ученик знает наудачу
вытянутый билет?
1)
1/6 2) 5/6 3) 1/3
4) 2/3
Вариант
17
В
ящике 6 апельсинов и 5 лимонов.
Наудачу достают одну штуку. Найти
вероятность того, что отобран
лимон. 1)
5/11
2) 5/6
3)
6/5
4) 1/6
2.
На шести карточках написаны буквы
А, В, К, М, О, С. После перемешивания
вынимают наугад одну карточку за
другой и раскладывают по порядку.
Найти вероятность того, что при
этом получится слово «МОСКВА».
1) 1 2) 1/720 3) 1/365 4) 1/5
3.
Дискретная случайная величина Х
задана рядом распределения. Найти
D(Х)/
1)
4,19 2) 3,85 3) 0,27
4) ‒1,57
4.
Из большой партии изготовленных
валиков по выборке объема
 найдена выборочная средняя
арифметическая диаметра валика,
равная 10 мм. Считая, что диаметр
валика X
– нормально распределенная СВ,
найти доверительный интервал,
который с доверительной вероятностью
0,99 покрывает неизвестное математическое
ожидание а
диаметра валика, если генеральное
среднее квадратическое отклонение
найдена выборочная средняя
арифметическая диаметра валика,
равная 10 мм. Считая, что диаметр
валика X
– нормально распределенная СВ,
найти доверительный интервал,
который с доверительной вероятностью
0,99 покрывает неизвестное математическое
ожидание а
диаметра валика, если генеральное
среднее квадратическое отклонение
 мм.
мм.
1)
(9,9532;10,0468)
2) (8,1232;9,7134)
3) (11,2532;12,7138)
4)
(9,3281;10,6829)
5.
В среднем 20% акций на аукционе
продается по первоначально заявленной
стоимости. Найти вероятность того,
что из четырех пакетов акций в
результате торгов будут проданы
не менее двух пакетов акций.
1) 0,1808
2) 0,4237
3) 0,5563
4) 0,9873
Вариант
18
На
собеседование пришли 8 секретарей
и 7 бухгалтеров. Отобран для работы
один человек. Найти вероятность
того, что отобран секретарь, если
отбор был случайным.
7/8
2) 7/15
3) 8/15
4) 8/7
Два
стрелка производят по одному
выстрелу. Вероятность попадания
в цель для первого и второго стрелков
равны 0,8 и 0,75, соответственно.
Найти вероятность поражения цели.
1)
0,2
2) 0,95
3) 0,75
4) 0,6
3.
Найдите, используя график плотности,
вероятность попадания случайной
величины X
в интервал (0, 2).

1)
5/3
2) 1/2
3) 1/3
4) 2/3
4.
Произведено 5 независимых наблюдений
над СВ X
~ N
(a,
20).
Результаты наблюдений таковы:
= − 25,
= 34,
= − 20,
=
10,
= 21. Построить 95 %-й доверительный
интервал для генеральной средней.
1)
(2,31; 4,58)
2) (‒
0,56; 10,56)
3) (4,32;
6,97)
4)
(1,28; 3,25)
5.
В семье 4 ребенка. Считая, что
вероятность рождения мальчика
равна 0,5 , найти вероятность того,
что среди этих детей не менее 2-х
мальчиков.
1)
0,8155
2) 0,5
3) 0,3128
4) 0,6875
Вариант
19
Из
колоды карт (их 36) наугад вынимают
одну карту. Найти вероятность того,
что эта карта будет шестеркой.
1)
1/36
2) 1/18
3) 1/6
4) 1/9
2.
Баскетболист дважды бросает мяч
в корзину. Вероятность попадания
при первом броске равна 0,6, а при
втором - 0,8. Какова вероятность того,
что цели достигнет только первый
бросок?
1)
0,6
2) 0,12
3) 0,48
4)
1,4
3. Следующая таблица представляет
распределение годовой прибыли
фирмы:
X
|
−10
|
− 5
|
0
|
10
|
20
|
p
|
0,1
|
0,15
|
0.25
|
0,3
|
0,2
|
Найти
вероятность того, что фирма будет
терпеть убытки.
1)
0,25
2) 0,1
3) 0,15
4) 1
4.
Из большого количества деталей
отобрано 100, распределение которых
по размеру задано в таблице.
Размер
детали
|
8
–8,2
|
8,2
– 8,4
|
Количество
|
20
|
80
|
Найти
реализацию оценки дисперсии. 1)
0,0064 2) 0,0035 3) ‒ 0,002 4) 0,0025
5.
Дана функция распределения СВ X:
F(x)
=

Найти
вероятность того, что СВ примет
значение между числами 0,5 и 10.
1)
0,125
2) 1
3) 0,235
4) 0,875
Вариант
20
1.
Участники жеребьевки тянут из
ящика жетоны с номерами от 1 до 100.
Найти вероятность того, что номер
первого наудачу извлеченного жетона
содержит цифру 0.
1)
0,4
2) 0,3
3) 0,2
4) 0,1
2.
Вероятность того, что ученик сдаст
первый экзамен равна 0,9; второй –
0,8. Какова вероятность того, что
ученик сдаст ровно один экзамен?
1)
0,26
2) 0,72
3) 0,9
4) 0,18
3.
СВ
имеет нормальный закон распределения
с параметрами: a
= 8,6;
 = 0,5.
= 0,5.
Найти
вероятность того, что она примет
какое-нибудь значение, большее 9.
1)
0,5
2)
0,6528
3) 0,2881
4) 0,2119
4.
СВ X распределена по нормальному
закону. Статистическое распределение
выборки представлено в таблице.
Найти несмещенную выборочную оценку
для D(X).
1)
‒
0,25
2) 0,11
3) 0,32
4)
7,6
5.
Найти 95%-ный доверительный интервал
для матожидания СВ
X
на основании данного распределения
выборки:
1)
(2,051; 3,225) 2) (3,855; 6,145) 3) (‒
1,278; 3,577)
4)
не
существует
|


