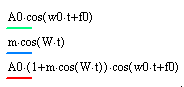Лекция 4

3.5 Преобразования электромагнитных колебаний

3.5.1 Модуляция

Изменение параметров колебания во времени по определенному закону называется модуляцией, а устройства его осуществляющие – модуляторами. В соответствии с видом модулируемого параметра ( , 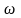или ) различают амплитудную (АМ), частотную (ЧМ) и фазовую (ФМ) модуляции.

Закон изменения параметров в простейшем случае может быть гармоническим. При этом модулируемый параметр 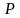может быть представлен в следующем виде

(3.15)

где 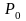- соответствующий параметр немодулируемого колебания;

- амплитуда изменения параметра;

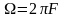- круговая частота модуляции;

- частота модуляции;

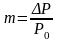- коэффициент модуляции.

Модуляцию по прямоугольному закону называют манипуляцией.

ЧМ и ФМ неразрывно связаны друг с другом: при изменении частоты меняется фаза колебания и наоборот. Поэтому иногда эти виды модуляции объединяют под названием «угловая модуляция»

Частоту модулируемого колебания 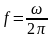называют несущей частотой, а само колебание – несущим колебанием. При этом обычно несущая частота намного больше частоты модуляции, т.е. 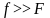, соответственно .

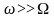При модуляции света часто применяют еще один вид модуляции – поляризационную, при которой изменению подвергается состояние поляризации света.

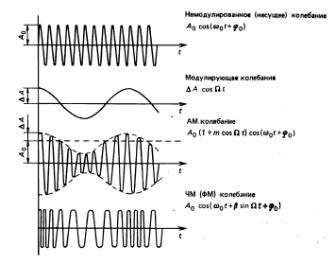
Модуляция по гармоническому закону (рис. 3.16) наиболее часто применяется в дальномерных устройствах.

Рис. 3.16 – Модуляция колебаний гармоническим сигналом

Пусть немодулированное колебание имеет вид

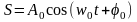(3.16)

3.5.1.1 Амплитудная модуляция

При гармонической амплитудной модуляции в соответствии с (3.32) амплитуда меняется во времени по закону

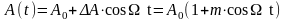(3.18)

и уравнение АМ колебания будет иметь вид

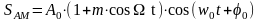(3.19)

где 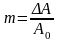- называется коэффициентом амплитудной модуляции.

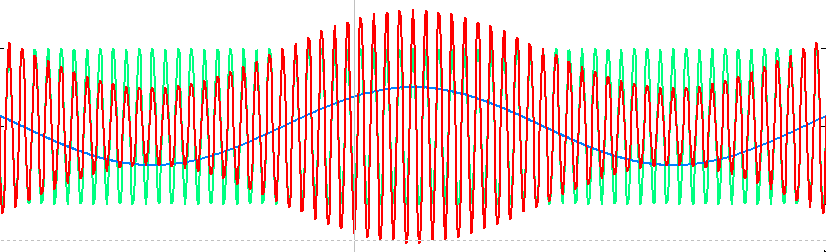
На рис. 3.17 показан пример амплитудной модуляции.

Рис. 3.17 – Пример амплитудной модуляции

3.5.1.2 Частотная модуляция

При гармонической частотной модуляции имеем

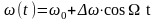(3.20)

Если частота – функция времени, то в уравнении (3.16) вместо 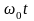надо записать 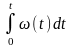(пояснить, почему) и, следовательно, уравнение ЧМ колебания будет иметь вид

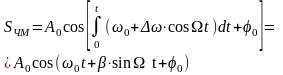(3.21)

где величина называется индексом частотной модуляции, а 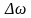- девиацией частоты. (Девиация – отклонение).

На рис. 3.18 показан пример частотной модуляции.

Рис. 3.18 – Пример частотной модуляции

3.5.1.3 Фазовая модуляция

При гармонической фазовой модуляции вместо начальной фазы в уравнении (3.16) надо записать

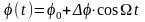, (3.22)

и, следовательно, уравнение ФМ колебания будет иметь вид

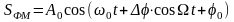, (3.23)

где - девиация фазы, т.е. максимальное отклонение фазы от среднего значения. Девиацию фазы также называют индексом фазовой модуляции.

Из сравнения уравнений (3.21) и (3.23) видна общность частотной и фазовой модуляций. Поэтому ФМ колебания можно рассматривать как ЧМ колебание, в котором, однако, частота изменяется в соответствии не с модулирующим колебанием, а с его производной по времени. Точно так же ЧМ колебания можно рассматривать как ФМ колебание, в котором фаза изменяется в соответствии не с модулирующим колебанием, а с его интегралом по времени.

На рис.3.19 показан пример фазовой модуляции.

Рис. 3.19 – Пример фазовой модуляции