Контрольні питання

1. Яка пара є вологою насиченою парою?

2. Що таке „ступінь сухості насиченої пари”?

3. Яка пара є сухою насиченою парою?

4. Яка пара є перегрітою водяною парою?

5. Як записати рівняння Клайперона – Клаузіуса?

6. Що таке „прихована теплота пароутворення”?

7. Що називається „фазовою діаграмою”?

8. Які є методи визначення ступеня сухості вологої насиченої пари?

9. Як визначається питомий об'єм, ентальпія, внутрішня енергія та ентропія вологої насиченої пари?

Лабораторна робота №4

ВИЗНАЧЕННЯ ВІДНОШЕННЯ|ставлення| ТЕПЛОЕМКОСТЕЙ| ГАЗУ

ЗА МЕТОДОМ КЛЕМАНА-ДЕЗОРМА|

Мета роботи: Метою|ціллю||теперішньої,даної| роботи є|з'являється,являється| вивчення процесів, що відбуваються|походять| в газі при вимірюванні|вимірі| відношення|ставлення| питомих теплоємностей|

Обладнання:

Теоретична частина

Питомою теплоємністю газу називається кількість тепла, необхідне для нагрівання одиниці маси газу на один градус. Величина теплоємності газів залежить від умов їх нагрівання.

Запишемо перший початок термодинаміки:

dQ = dU + dA

(1)

де dQ – кількість тепла, що підводиться до термодинамічної системи і витрачається на збільшення її внутрішньої енергії dU і на роботу dA, що здійснюється|скоюється,чиниться| системою проти|супроти| зовнішніх сил.

За визначенням теплоємності

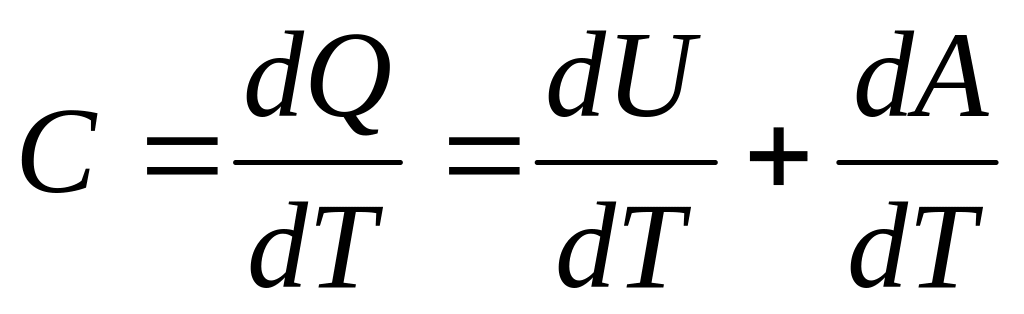
(2)

де елементарна робота dA = pdV

Розглянемо|розгледимо| два випадки:

1. Газ нагрівається при незмінному об'ємі|обсязі| V = const.

В цьому випадку dV = 0 і робота зовнішніх сил рівна нулю dA = pdV = 0, отже, все передане газу ззовні тепло йде на збільшення його внутрішньої енергії dU. Тоді з|із| рівняння (2) виходить, що теплоємність при постійному об'ємі|обсязі| рівна:

.

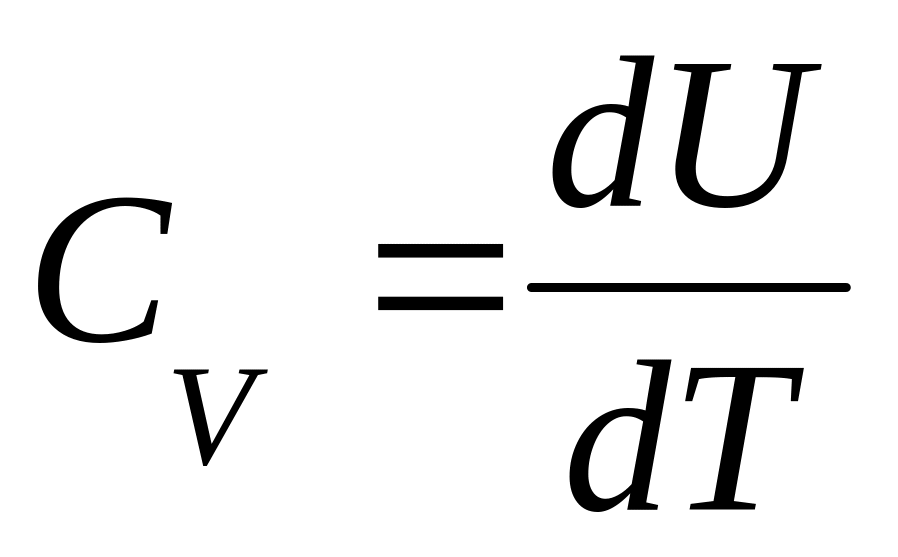(3)

2. Газ нагрівається при постійному тиску|тисненні| p = const.

В цьому випадку отримане|отримуване| газом ззовні тепло йде не тільки|не лише| на збільшення його внутрішньої енергії dU, але і на здійснення газом роботи dA проти|супроти| зовнішньої сили тиску|тиснення|. Тоді теплоємність при постійному тиску|тисненні| рівна:

.

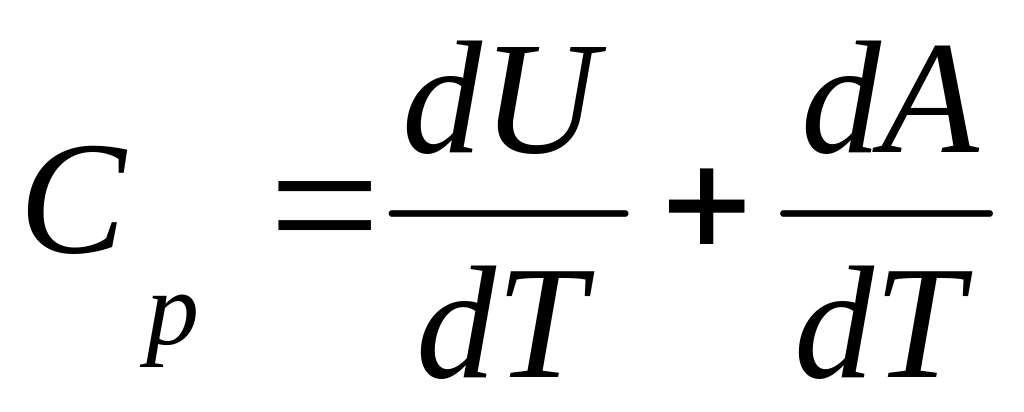(4)

Отже, для нагрівання одиниці маси газу на один градус при p = const буде потрібно більше тепла, ніж при V = const.

Знайдемо зв'язок між С_р і С_v.

Скориставшись рівнянням стану ідеального газу для одиниці маси ідеального газу, отримаємо|отримаємо|:

(5)

При p = const, dp = 0, і тоді

Підставивши цей вираз в (4) і замінивши dU/dT на C_v згідно (3) (для одиниці маси), отримаємо|отримаємо|:

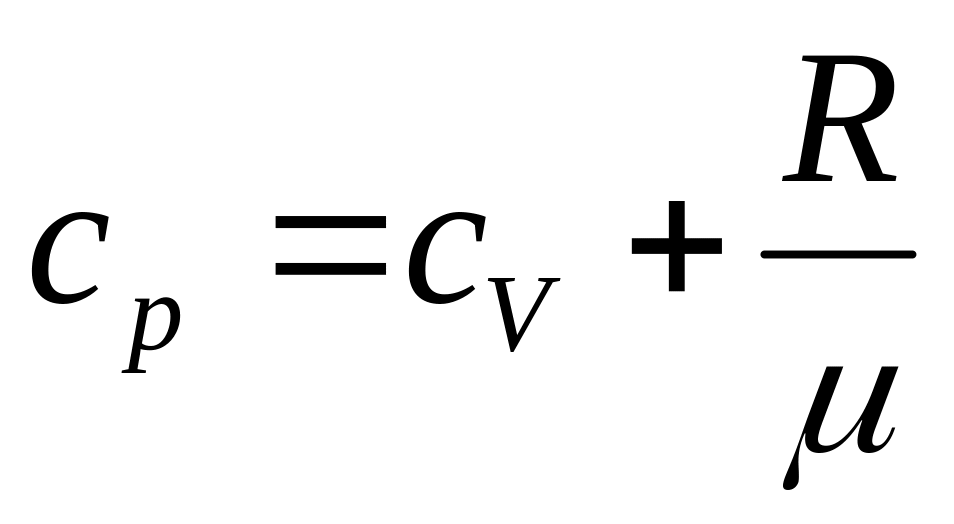
(6)

Таким чином, питома теплоємність С_р більше питомої теплоємності С_v на величину R/μ, яка є роботою, що здійснюється|скоюється,чиниться| одиницею маси газу при розширенні, що відбувається|походить| при постійному тиску|тисненні| в результаті|унаслідок,внаслідок| підвищення його температури на один градус.

Разом з|поряд з,поряд із| питомою теплоємністю с|із|, часто користуються молярною теплоємністю C (теплоємність одного кіломоля речовини). Між ними є|наявний| очевидне співвідношення

Тоді співвідношення (6) можна записати у вигляді|виді|:

Згідно закону рівнорозподілення| енергії за ступенями вільності на кожну ступінь вільності молекули ідеального газу доводиться|припадає,приходиться| в середньому однакова енергія, рівна 1/2kT (k – постійна Больцмана). Тому внутрішню енергію одного кіломоля ідеального газу можна знайти за формулою:

,

де N_А – число Авогадро, i – число ступенів вільності молекули газу.

Підставивши цей вираз в (3), отримаємо|отримаємо|:

Число ступенів вільності визначається числом атомів в молекулі і характером|вдачею| зв'язку між ними. Для одноатомного газу i = 3; для двоатомного – i = 5 (жорсткий зв'язок), i = 6 (пружний зв'язок); для трьох і більш атомів в молекулі i = 6 (жорсткий зв'язок, нелінійна молекула).

Оскільки|тому що|

або

то

або

і

Величини c_p і c_v можна визначити експериментально. Проте|однак| існує спосіб безпосереднього визначення відношення|ставлення| c_p/c_v = γ яке залежить тільки|лише| від числа ступенів вільності молекул газу. Це відношення|ставлення| входить у вираз|вираження| закону Пуассона, що описує адіабатичний процес в газах.

PV2 = const

(7)

Адіабатичним процесом називається процес, що протікає без теплообміну з|із| навколишнім середовищем.

Такий процес відбуватиметься|походитиме| в системі, оточеній абсолютно|цілком| нетеплопровідними стінками. Оскільки|тому що| абсолютно|цілком| нетеплопровідних стінок не буває, реально процес може лише наближатися до адіабатичного. Якщо процес протікає достатньо|досить| швидко, так що система не встигає|устигає| вступити в теплообмін з|із| навколишнім середовищем, то його можна рахувати практично адіабатичним і за відсутності хорошої|доброї| теплової ізоляції (наприклад, при швидкому стисненні|стискуванні| або розширенні газу).

Перший початок термодинаміки для адіабатичного процесу приймає вигляд|вид|:

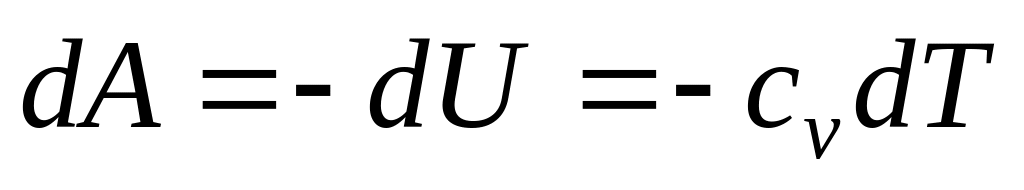
(8)

тобто|цебто| при адіабатичному розширенні робота здійснюється|скоюється,чиниться| газом тільки|лише| в результаті|унаслідок,внаслідок| зміни запасу його внутрішньої енергії. Адіабатичне розширення супроводжується|супроводиться| пониженням температури, а адіабатичне стиснення|стискування| – підвищенням температури.

Виведемо рівняння адіабатичного процесу (рівняння Пуассона).

Оскільки dA = pdV, то, використавши вираз|вираження| (8), знайдемо

.

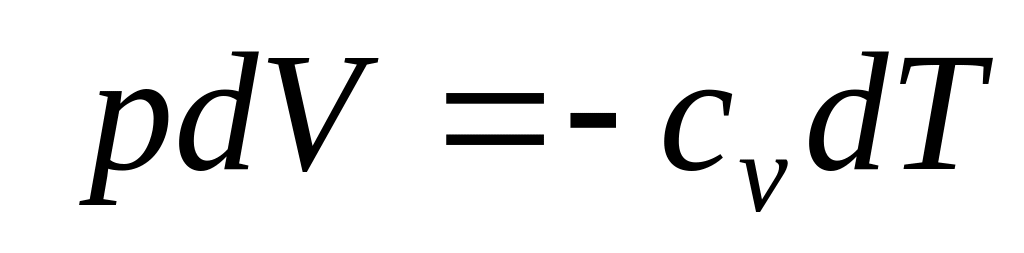(9)

Поділивши рівняння (5) на (9) і взявши до уваги, отримаємо|отримаємо|

звідки

(10)

де

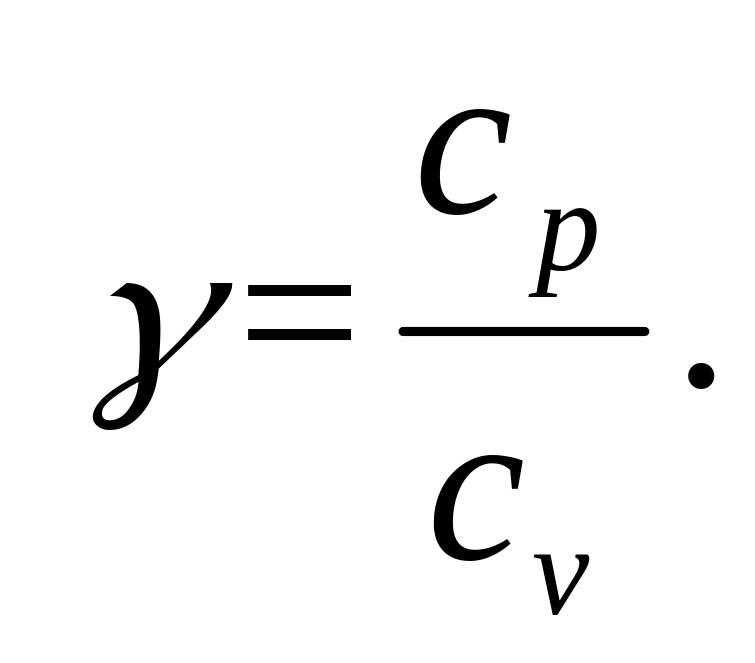
(11)

Після|потім| інтеграції і потенціювання (10) одержимо|отримаємо| рівняння Пуассона

PV² = const

Прилад Клемана-Дезорма, за допомогою якого можна визначити величину с_р/с_v (рис4.1). Він є балоном (1) на 10 л з|із| повітрям, яке накачується ручним насосом (2) до деякого тиску|тиснення| p, надлишок якого h = p – p₀ над атмосферним p₀ визначається по водяному манометру (3), який сполучається з балоном (1) гумовим шлангом (4).

Для здійснення швидкого (адиабатного|) розширення повітря з|із| балона (1) до атмосфери служить клапан (5).

Рис.4.1. Схема установки Клемона – Дезорма для визначення відношення теплоємностей газу

1- балон; 2 – ручний насос; 3 - водяний манометр; 4 – гумовий шланг; 5 – клапан.

Виділимо (у думках) усередині повітря, що знаходиться|перебуває| в балоні (1), деяку масу m і простежимо за зміною її стану під час експерименту|досліду| при одночасній зміні тиску|тиснення| p і температури T.

Якщо клапан (5) відкритий|відчинений|, то тиск|тиснення| в судині|посудині| рівний атмосферному P₀; температура повітря в судині|посудині| рівна T₀ – температурі навколишнього середовища. Тоді параметрами виділеної в думках маси повітря будуть, V₀, T₀, P₀ де V₀ – об'єм|обсяг| даної маси повітря при тиску|тисненні| P₀ і температурі T₀.

Якщо тепер закрити|зачинити| клапан (5) і накачати за допомогою насоса в судину|посудину| деяку кількість повітря, то маса повітря, що розглядається|розглядується| нами, стиснеться|стискуватиметься|, а температура і тиск|тиснення| її підвищаться. Через деякий час у наслідок|внаслідок| теплообміну з|із| навколишнім середовищем температура повітря в судині|посудині| стане рівною T₀. Тиск|тиснення| же буде рівний:

,

(12)

де h₁ – остаточна (після|потім| встановлення теплової рівноваги з|із| навколишнім середовищем) різниця рівнів рідини в манометрі. Стан даної маси повітря визначається тепер параметрами V₁ , P₁ , T₀ – це I стан виділеної маси повітря; V₁ – об'єм|обсяг| даної маси повітря при тиску|тисненні| P₁ і температурі T₀.

Якщо на короткий час ( 1-2 с|із|) відкрити|відчинити| клапан (5), то повітря, що знаходиться|перебуває| в балоні, швидко (за адіабатою) розшириться і внаслідок цього охолоджується. В кінці|у кінці,наприкінці| цього малого проміжку часу, протягом якого клапан (5) відкритий|відчинений|, і балон сполучається з атмосферою, тиск|тиснення| повітря у середині судини|посудини| стане рівним тиску|тисненню| атмосфери, і стан даної маси повітря визначатиметься у цей момент наступними|такими| параметрами, V₂, P₀ , T₁– це II стан виділеної маси повітря;

V₂ – об'єм|обсяг| даної маси повітря при тиску|тисненні| P₀ і температурі T₁. При цьому < .

Коли тиск|тиснення| в судині|посудині| (1) стане|чинитиметься| рівним тиску|тисненню| атмосфери P₀ (через 1-2 с|із|), клапан (5) закривають|зачиняють|. Повітря, що знаходиться|перебуває| в балоні (1), починає|розпочинає,зачинає| нагріватися від T₁ до T₀ у наслідок|внаслідок| отримання|здобуття| тепла від навколишнього середовища, тиск|тиснення| в судині|посудині| починає|розпочинає,зачинає| підвищуватися і стане рівним:

,

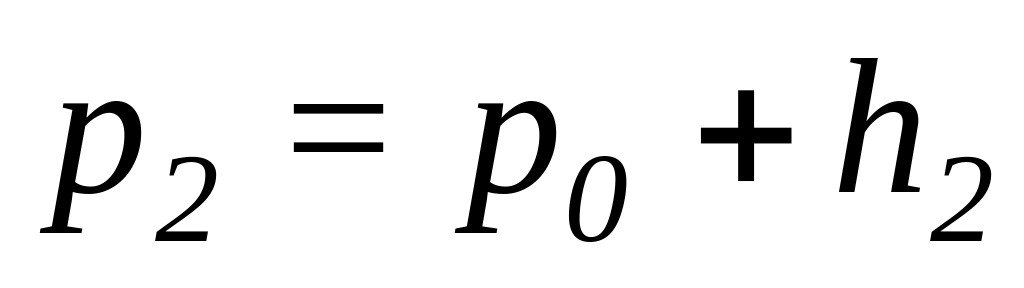(13)

де h₂ – різниця рівнів рідини в манометрі після того, як температура газу в балоні стане рівній температурі навколишнього середовища.

Дана маса повітря тепер характеризується параметрами V₂ , P₂ , T₀ – це III стан даної маси повітря.

Отже, дана маса повітря під час експерименту знаходилася|перебувала| послідовно в трьох станах:

I.	V1,	P1,	T0
II.	V0,	P0,	T1
III.	,	P2,	T0

Перехід із стану I в стан II відбувається адіабатно, із стану II в – стан III – ізохорно.

Рис.4.2 .Графіки процесів.

На Рис4.2. зображені|змальовані| графіки процесів: крива I-II – адіабата, крива II-III – ізохора, крива III-I – ізотерма. Газ в станах I-III має однакову температуру.

Перехід із|із| стану I в стан II описується рівнянням Пуассона:

(14)

Параметри станів I і III задовольняють закону Бойля-Маріотта:

.

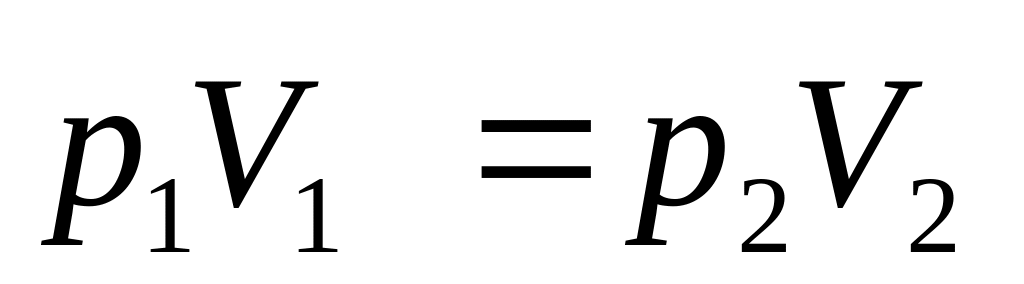(15)

Піднісши рівняння (15) до ступеня  і розділивши його за членами| на (14), отримаємо|отримаємо|:

,

Звідси

,

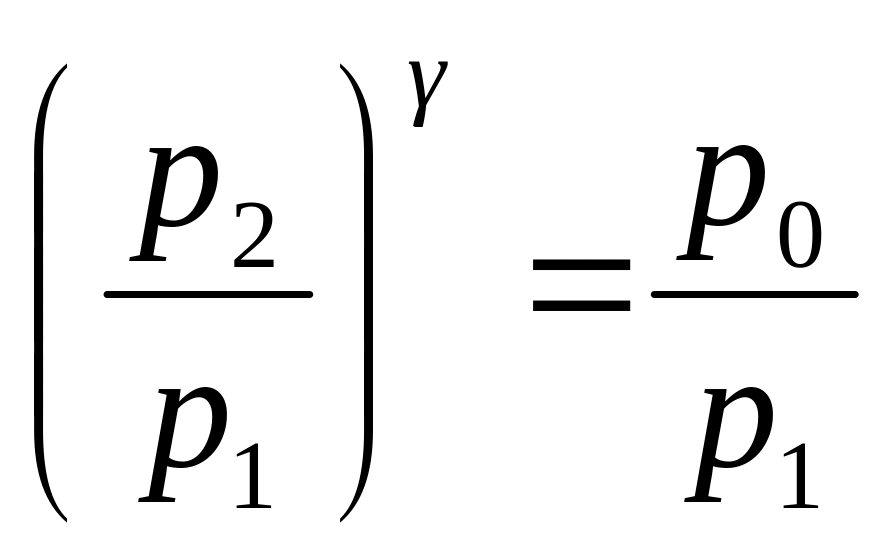(16)

Враховуючи рівність (12) і (13), отримаємо|отримуємо|, що

,

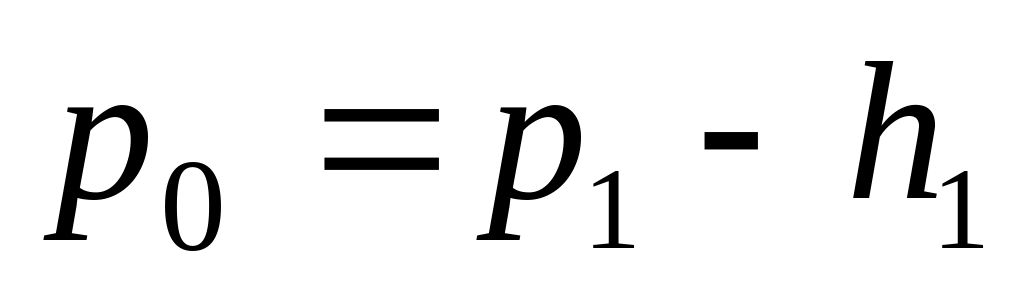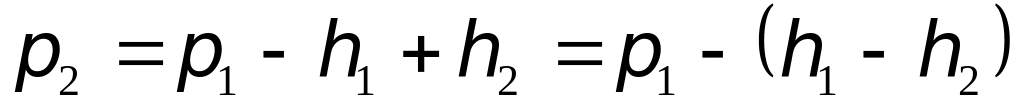
і, підставляючи їх в рівність (16), маємо

(17)

Оскільки|тому що| h₁ – h₂  p₁, то, розклавши в ряд|лаву,низку| ліву частину|частку| (17) і обмежившись першим членом розкладання, отримаємо

|отримаємо|

.

(18)

Прирівнявши праві частини|частки| (17) і (18), отримаємо|отримаємо| наступну|слідуючу| формулу:

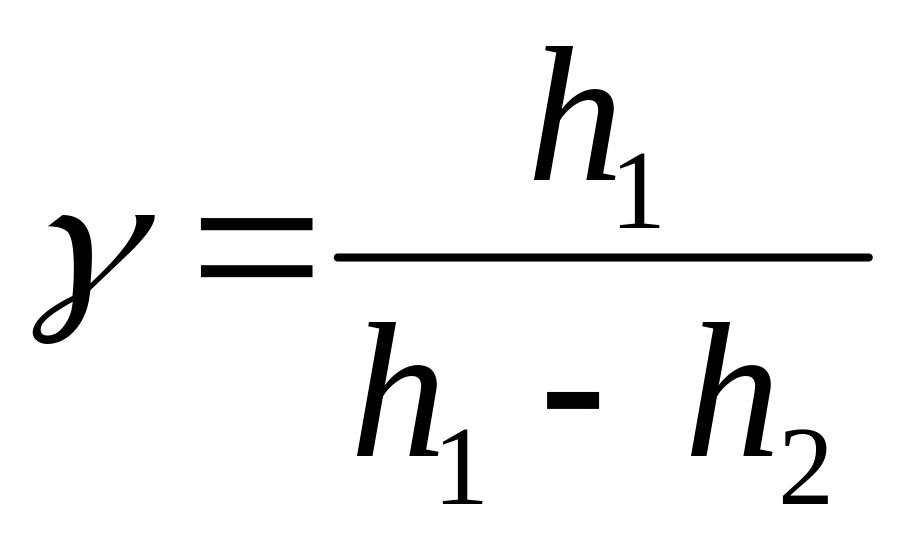
(19)

яка і використовується в цій роботі для експериментального визначення .