
Обобщение понятие степени Корень n-степени
Корнем
n-степени
из числа
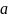 называется такое число,
n-степень
которого равна
.
называется такое число,
n-степень
которого равна
.
Арифметическим
корнем натуральной степени
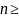 2
из неотрицательного числа
называется неотрицательное число,
2
из неотрицательного числа
называется неотрицательное число,
 - я степень которого равна
.
- я степень которого равна
.
Арифметический
корень
n-степени
из числа
обозначается так:
 .
Число
называется подкоренным выражением.
Если
=2,
то вместо
.
Число
называется подкоренным выражением.
Если
=2,
то вместо
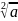 пишут
пишут
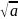 .
.
Арифметический корень второй степени называют также квадратным корнем, а корень третьей степени – кубическим корнем.
Действие, посредством которого отыскивается корень, -й степени, называется извлечением корня -й степени. Это действие является обратным действию возведения в -й степень.
Для
любого нечетного натурального числа
2k+1
уравнение
 имеет
только один корень, причем отрицательный.
Этот корень обозначается, как и
арифметический корень, символом
имеет
только один корень, причем отрицательный.
Этот корень обозначается, как и
арифметический корень, символом
 Его
называют корнем
нечетной степени из
отрицательного числа.
Его
называют корнем
нечетной степени из
отрицательного числа.
Пример:
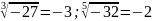
Корень
нечетной степени из отрицательного
числа
связан с арифметическим корнем
из
числа
-
= следующим равенством
следующим равенством
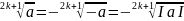
Пример:

Основные свойства корней
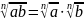
 =
=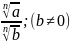
 (
(
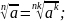 (
(
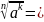 (
(
Степень рациональным показателем
Степенью
числа
 с рациональным показателем
с рациональным показателем
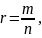 где m
– целое число, а
где m
– целое число, а
n
– натуральное (n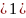 ,
называется число
,
называется число
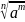
по
определению:
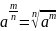
Для
любых рациональных чисел и
любых положительных чисел
и
любых положительных чисел
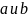 справедливы равенства:
справедливы равенства:




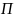 усть
усть
 рациональное число
и
рациональное число
и
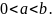 Тогда
Тогда
 при
при

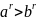 при
при
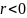
Для
любых рациональных чисел
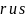 из неравенства
из неравенства
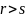 следует, что
следует, что
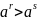 при
при
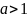 ,
,
 при
при
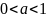
Степень с действительным показателем
При
любом
 и
любом
степень
и
любом
степень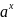 является положительным действительным
числом:
является положительным действительным
числом:
 при
при

Для
любого
и любого
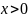 число
больше 1, то есть
число
больше 1, то есть
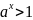 при
при
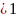 ,
,
Пусть
и
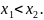 Тогда
Тогда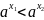 .
.
Пусть
и
Тогда
Пусть
 ,
,
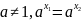 .
Тогда
.
Тогда
 .
.
Пусть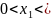
 .
Тогда если
.
Тогда если
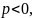 то
то
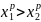 .
.
При возведении неравенства с положительной левой и положительной правой частями в положительную степень знак неравенства не меняется, а при возведении в отрицательную степень знак неравенства меняется на противоположный.
Логарифмы
Логарифмом
положительного числа
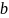 по основанию
,
где
по основанию
,
где
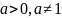 ,
называется показатель степени, в которую
надо возвести число
,
чтобы получить число
.
,
называется показатель степени, в которую
надо возвести число
,
чтобы получить число
.
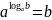
основным логарифмическим тождеством)
Десятичным
логарифмом числа называют
логарифм этого числа по
основанию
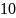 и
пишут
и
пишут
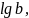 вместо
вместо
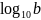
Натуральным
логарифмом числа называют
логарифм этого числа по
основанию
 где
где
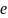 – иррациональное число, приближенно
равное
2,7.
При этом пишут
– иррациональное число, приближенно
равное
2,7.
При этом пишут
 вместо
вместо

Свойства логарифмов
Пусть
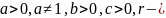 действительное
число. Тогда справедливы формулы:
действительное
число. Тогда справедливы формулы:
1.
2.
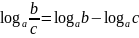
3.
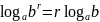
4.
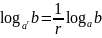
5.
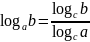 , (где
, (где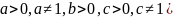
(формула перехода от логарифма по одному основанию к логарифму по другому основанию)
Показательная функция
Функция,
заданная формулой
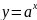 ,
(где
,
(где
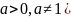 ,
называется показательной функцией с
основанием
,
называется показательной функцией с
основанием
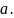
Свойства показательной функции:
Область определения – множество R всех действительных чисел
D(
)
= (-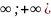
Область значения – множество R+ всех положительных чисел
E(
) = (0;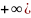
Показательная функция является возрастающей на множестве всех действительных чисел, если , и убывающей, если
Значения функции - положительны
График любой показательной функции проходит через точку с
координатами (0;1)
Логарифмическая функция
Функция,
заданная формулой
 ,
называют логарифмической функцией с
основанием
.
,
называют логарифмической функцией с
основанием
.
Свойства логарифмической функции:
Область определения – множество R+ всех положительных чисел
D
(
 )
= (0
)
= (0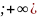
Область значения – множество R всех действительных чисел
E
(
) = ( ;
;
Логарифмическая функция является возрастающей на промежутке , если , и убывающей, если
Если
,
то
функция
принимает
положительные значения
при
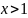 ,
отрицательные при
,
отрицательные при
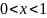 .
Если
,
то
функция
принимает
положительные значения при
,
отрицательные при
.
Если
,
то
функция
принимает
положительные значения при
,
отрицательные при
График любой логарифмической функции проходит через точку
с координатами (1;0)
