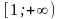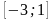- •III. Выявление основных свойств функций.
- •Организация записей как компетенция
- •Задание
- •Элемент математической культуры как компетенция
- •Организация записей как компетенция
- •Задание
- •Организация записей как компетенция
- •Задание
- •Задание
- •IV. Способы построения графиков.
- •Задание
- •По теме «Функции в шкм» нужно знать алгоритмы:
Задание
Составьте план нахождения промежутков возрастания (убывания) функции с использованием производной.
1. _______________________________________________________________________
2. _______________________________________________________________________
3. _______________________________________________________________________
Организация записей как компетенция
Используйте скобки для отражения взаимосвязанных утверждений.
5. Определение знаков функции.
Чтобы найти знаки функции у = f(x), надо составить и решить неравенства:
f(x) _________; f(x) ____________.
6. Исследование функции на четность (нечетность).
Чтобы исследовать функцию на четность (нечетность), нужно в формулу функции вместо х подставить –х (составить формулу f(–x)) и преобразовать полученное выражение; если в результате преобразований получится f(x), сделать вывод, что функция является четной; если в результате преобразований не получится f(x), то вынести знак «–» за скобки; если в результате таких преобразований получится –f(x), сделать вывод, что функция является нечетной.
Если хотя бы при одном х D(f) либо –х не входит в область определения функции f, либо не выполнено равенство f(–x) = –f(x) или f(–x) = f(x), то сделать вывод, что функция свойством четности, свойством нечетности не обладает.
Задание
Выделите план исследования функции на четность (нечетность) в предложенном тексте.
7. Исследование функции на периодичность.
В вводном курсе математики такое исследование проводится только для тригонометрических функций на основе следующей теоремы.
Теорема. Если функция f периодична и Т – ее период, то функция g(х) = f (kx), где k – не равное 0 целое число, также периодичная с периодом Т/k.
Например. Для функции g(x) = sin 5x период Т равен _______.
8. Исследование функции на экстремумы, на наибольшее и наименьшее значения.
Исследование функции на экстремумы соединяют с исследованием функции на монотонность; при этом пользуются следующей схемой.
Схема исследования функции на монотонность и экстремумы с помощью производной
1) Найти производную функции.
2) Найти на области определения функции нули производной и те точки, где производная не существует (такие точки называют критическими).
3) Изобразить числовую прямую и область определения функции, если она имеет ограничения. Отметить на области определения точки, в которых производная либо не существует, либо обращается в нуль. Полученными точками область определения разбивается на промежутки знакопостоянства производной.
4) На каждом из полученных промежутков определить знак производной.
5) На каждом из полученных промежутков определить характер монотонности функции.
6) Определить точки максимума функции (точки, в которых возрастание функции сменяется убыванием) и точки минимума (точки, в которых убывание функции сменяется возрастанием). Найти значение функции в точках экстремума.
Задание
Реализуйте схему исследования функции на монотонность и экстремумы на примере функции f (x) = х3 + 3х2 – 9х + 1.
Шаги |
Реализация шагов на примере |
|
|
f (x) = |
|
|
f (x) = 0; = 0; = 0; х1 = ; х2 = . |
|
|
х
|
|
|
|
|
|

Функция возрастает на
Функция убывает на
|
|
|
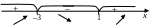
___ – точка максимума; f (__) = (__) 3 + 3 (__) 2 – 9 (__) + 1 = ______________ = __. __ – точка минимума; f (_) = _________________________________________= ___.
|
При исследовании непрерывной функции на наибольшее и/или наименьшее значение на заданном отрезке пользуются следующей схемой.
Схема исследования функции на наибольшее и наименьшее значения на заданном отрезке
а) Найти критические точки функции.
б) Выбрать критические точки, принадлежащие заданному промежутку; вычислить значение функции в этих точках и на концах заданного отрезка.
в) Выбрать из полученных чисел наибольшее и наименьшее.
Самостоятельно: Найти
наибольшее и наименьшее значения функции
f (x)
= х3 + 3х2 – 9х
+ 1 на отрезке
 .
.
Замечание. Пользуясь этим исследованием, можно определить область значений функции, так как если функция непрерывна на отрезке, то она на нем достигает своего наименьшего и наибольшего значения.




 f
(0) = –9; –9 < 0
f
(0) = –9; –9 < 0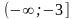 и
и