
- •III. Выявление основных свойств функций.
- •Организация записей как компетенция
- •Задание
- •Элемент математической культуры как компетенция
- •Организация записей как компетенция
- •Задание
- •Организация записей как компетенция
- •Задание
- •Задание
- •IV. Способы построения графиков.
- •Задание
- •По теме «Функции в шкм» нужно знать алгоритмы:
Лекция № 6-7. Функции в ШКМ (часть 2)
III. Выявление основных свойств функций.
Замечание. Графический способ выявления свойств функций см. в пункте I.
1. Нахождение области определения функции.
Элемент математической культуры как компетенция
ЭМК О структурном анализе математических объектов
В математике анализ объектов чаще всего начинают с анализа его структуры.
Поэтому нахождение области определения функции лучше всего начинать с вопроса: «Как устроена функция?».
Задание
По математическому тексту следующей части лекции о нахождении области определения функции определите ключевые слова, задающие структуру функции.
а)
 функций определены для тех значений
аргумента, для которых определены все
функций определены для тех значений
аргумента, для которых определены все
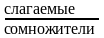 ,
т.е. область определения суммы или
произведения равна ______________________________
областей определения слагаемых или
сомножителей.
,
т.е. область определения суммы или
произведения равна ______________________________
областей определения слагаемых или
сомножителей.
Задание
Составьте план нахождения области определения функции в случае а).
1. _______________________________________________________________________
2. _______________________________________________________________________
3. _______________________________________________________________________
Пример. Найти область определения
функции f(x)
=
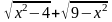
1. Арифметический квадратный корень
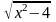 имеет смысл, если подкоренное выражение
неотрицательно, т.е. ________________________
имеет смысл, если подкоренное выражение
неотрицательно, т.е. ________________________
Решим неравенство х2 – 4 0.
Способ 1 (через преобразования) |
Способ 2 (методом интервалов) |
Способ 3 (графический) |
х2 ___; ______ 2;
|
Нули: х2 = 4; х =______ Интервалы, знаки, ответ:
_____________ |
Функция: у = х2 – 4. Ветви: Пересеч. с ОХ:
Решение: _____________ |
2. Арифметический квадратный корень
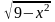 имеет
смысл, если подкоренное выражение
неотрицательно, т.е. 9 – х2
0.
имеет
смысл, если подкоренное выражение
неотрицательно, т.е. 9 – х2
0.
Решим неравенство 9 – х2 0.
_____________________________
3. Найдем пересечение решений:
 Ответ:
_____________________________
Ответ:
_____________________________
б) Частное двух функций определено для тех значений аргумента, для которых определены числитель и знаменатель и при этом значения знаменателя отличны от нуля.
Пример. Найти область определения
функции f(x)
=
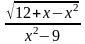 .
.
Удобно использовать следующую схему:
Выделить выражения, которые не всегда имеют смысл.
Определить условия, при которых выделенные выражения имеют смысл и записать их на языке неравенств.
Если условие одно, то решить неравенство; если условий несколько, то составить и решить систему неравенств.
Выражение |
условие |
неравенство |
|
имеет смысл, если
|
|
|
имеет смысл, если
|
|
Решим первое неравенство: Решим второе неравенство:


_____________ Ответ: _____________

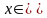 _____________
_____________
 График:
График: