
Упражнение № 4
Логические элементы И—НЕ и ИЛИ—НЕ называют базовыми, поскольку любой из перечисленных на рис. 5.1 логических элементов можно выразить только через И—НЕ (или ИЛИ—НЕ). Соответствующие схемы для одного из этих случаев приведены на рис. 5.1.

1)
Y
=

X |
X |
X+X |
X*X |
Y |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
2)
Y
=

Z
=
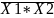
X1 |
X2 |
Z |
Y |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
3) =
=

Z
=

P
=

X1 |
X2 |
Z |
P |
Y |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
4) X1*X1 = A
X2*X2 = B
Z
=

P
=

Q
=

Y
=

X1 |
X2 |
A |
B |
Z |
P |
Q |
Y |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
Упражнение № 5
![]()

Рис. 5.4.
Задание 3. Проверить, что четырехвходовый элемент, изображенный на рис. 5.4, а, эквивалентен комбинации двухвходовых элементов, изображенной на рис. 5.4, б.
A)Y
=

B)


 =Y
=Y
Упражнение № 6

Задание 4.
Проверить, что имеют место логические формулы

