1. Тақырыбы: Кездейсоқ шамалар

2. Сағат саны – 2 сағат (80 мин).

3. Қажеттілігі (оқытудың мотивациясы):

Ықтималдықтар теориясы математикалық және қолданбалы статистиканың негізі болып табылады. Ал статистика өз кезегінде өндірісті жоспарлау мен ұйымдастыруда, технологиялық процестерді талқылауда, өнім сапасын тексеруге және басқа да мақсаттарда қолданылады. Кездейсоқ шамалар кездейсоқ оқиғалар құбылысын сипаттайтын сандар болып табылады.

4. Сабақтың мақсаты:

Кездейсоқ шамалардың ықтималдықтарының негізгі таралу заңдарымен таныстыру: Биномиалдық таралу, Пуассон таралуы, біркелкі таралу, қалыпты таралу. Қалыпты таралған кездейсоқ шаманың берілген аралыққа түсу ықтималдығы.

- студент білуі тиіс:

1. Биномиалдық таралу дегеніміз не?

2. Пуассон таралуы дегеніміз не?

3. Біркелкі таралу дегеніміз не?

4. Қалыпты таралу дегеніміз не?

5. Қалыпты таралған кездейсоқ шаманың берілген аралыққа түсу ықтималдығы.

- студент игеруі тиіс:

1. Биномиалдық таралуын табу

2. Пуассон таралуын табу

3. Біркелкі таралуын табу

4. Қалыпты таралуын табу

5. Қалыпты таралудың параметрлерін табу.

6. Қалыпты таралған кездейсоқ шаманың берілген аралыққа түсу ықтималдығын есептеу

5. Сабаққа дайындалуға арналған сұрақтар.

- базистік білім бойынша:

Кездейсоқ шаманың сандық сипаттамалары. Кездейсоқ шаманың таралу заңы. Үздіксіз кездейсоқ шаманың таралу функциясы және оның графигі. Дифференциалды таралу функциясы және оның графигі.

- сабақ тақырыбы бойынша:

1. Биномиалдық таралу дегеніміз не?

2. Пуассон таралуы дегеніміз не?

3. Біркелкі таралу дегеніміз не?

4. Қалыпты таралу дегеніміз не?

5. Қалыпты таралған кездейсоқ шаманың берілген аралыққа түсу ықтималдығы.

5. Ақпаратты- дидактикалық блок

Тақырып бойынша қысқаша теория:

Биномиалдық таралу, Пуассон таралуы, біркелкі таралу, қалыпты таралу. Қалыпты таралған кездейсоқ шаманың берілген аралыққа түсу ықтималдығын есептеу.

Биномиалдық таралу

n тәуелсіз сынақ жүргізілсін, әрбір сынақ нәтижесінде А оқиғасы пайда болуы мүмкін немесе пайда болмауы мүмкін. Әрбір сынаудағы оқиғаның пайда болу ықтималдығы тұрақты және р-ға тең (сәйкесінше оқиғаның пайда болмау ықтималдығы q=1-p) . Х дискретті кездейсоқ шамасын А оқиғасының осы жүргізілген сынақтағы пайда болу саны деп қарастыралық.

Х шамасының таралу заңын табайық. Мұны шешу үшін Х-тің мүмкін мәндерін және сәйкес ықтималдықтарын анықтау керек. А оқиғасы пайда болмауы мүмкін немесе 1 рет, 2 рет,..., немесе n рет пайда болуы мүмкін. Яғни х-тің мүмкін мәндері мынандай: х₁=0, х₂=1, х₃=2,..., х_n+1= n. Осы мүмкін мәндерінің сәйкес ықтималдықтарын табу үшін Бернулли формуласын қолданамыз:

(1)

мұнда к=0, 1, 2,..., n.

(1) формуласы іздеп отырған таралу заңының аналитикалық өрнегі болып табылады.

Анықтама. Ықтималдықтары Бернулли формуласымен анықталатын таралуды биномиалдық таралу деп атаймыз. Бұл заңның биномиалдық аталу себебі, (1) теңдігінің оң жақ бөлігін Ньютон биномының жіктелуінің жалпы мүшесі ретінде қарастыруға болады:

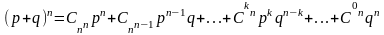
Яғни, жіктелудің бірінші мүшесі n тәуелсіз сынақта қарастырылып отырған оқиғаның n рет пайда болу ықтималдығын анықтайды; екінші мүшесі оқиғаның

n -1 рет орындалу ықтималдығын анықтайды; ...; соңғы мүшесі оқиғаның бір де бір рет орындалмау ықтималдығын анықтайды.

Биномиалдық таралу заңын кесте түрінде жазамыз:

Х	n	n-1	…	k	…	0
Р	Рn	pn-1q	…	Cknpkqn-k	…	qn

Мысал 1: Тиын екі рет лақтырылған. “Герб” түсу саны- Х кездейсоқ шамасының таралу заңын кесте түрінде жазу керек.

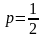Шешуі: Тиынды әрбір лақтырғанда “герб” түсуінің ықтималдығы , олай болса “герб” түспеуінің ықтималдығы .

Екі рет лақтырғанда “герб” 2 рет, немесе 1 рет, немесе мүлдем түспеуі мүмкін. Осылайша, Х-тің мүмкін мәндері: х₁=2, х₂=1, х₃=0 болады. Осы мүмкін мәндерінің ықтималдығын Бернулли формуласы бойынша табамыз:

Таралу заңын жазамыз:

Х	2	1	0
Р	0,25	0,5	0,25

Бақылау: 0,25+0,5+0,25=1.