Орта квадраттық ауытқу

Кездейсоқ шаманың орта мәнінің маңайындағы мүмкін болатын мәндердің шашылуын бағалау үшін сипаттамалар да қарастырылады. Оған орта квадраттық ауытқу жатады.

Анықтама: Х кездейсоқ шамасының орта квадраттық ауытқуы деп дисперсияның квадрат түбірін айтамыз:

.

Мысал 9. Х кездейсоқ шамасы мынадай таралу заңымен берілген:

Х	2	3	10
Р	0,1	0,4	0,5

орта квадраттық ауытқуын табу керек.

Шешуі: Алдымен Х-тің математикалық күтімін табамыз:

.

Одан кейін Х²-тің математикалық күтімін табамыз:

.

Дисперсия табамыз:

Сонда орта квадраттық ауытқуы .

Теорема: Өзара тәуелсіз кездейсоқ шамалардың ақырлы санының қосындыларының орта квадратық ауытқуы осы шамалардың орта квадраттық ауытқуларының квадраттарының қосындысынан квадрат түбір алғанға òå».

(4)

Таралу функциясы

Х кездейсоқ шамасының сан осінде х-тің сол жағында жататын мәндерді қабылдайтын ықтималдықты анықтайтын функциясын таралу функциясы деп атайды, яғни . (5)

Кейде “Таралу функциясы”(терминінің) орнына “Интегралдық функция” деген термин де қолданылады.

Таралу функциясының қасиеттері

1. Таралу функциясының мәндері [0; 1] аралығында жатады; .

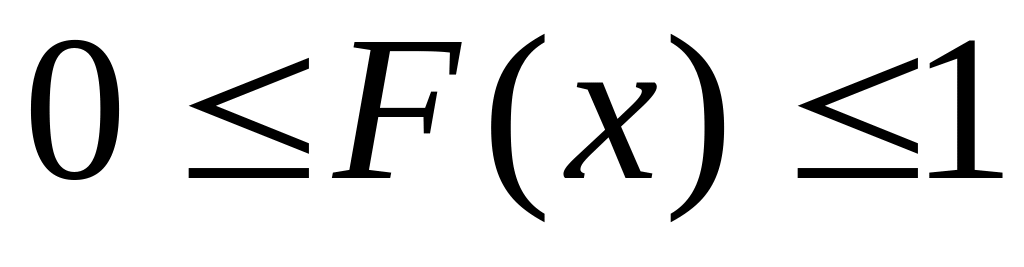2. F(x)-кемімейтін функция, егер х₂>x₁ болса, онда 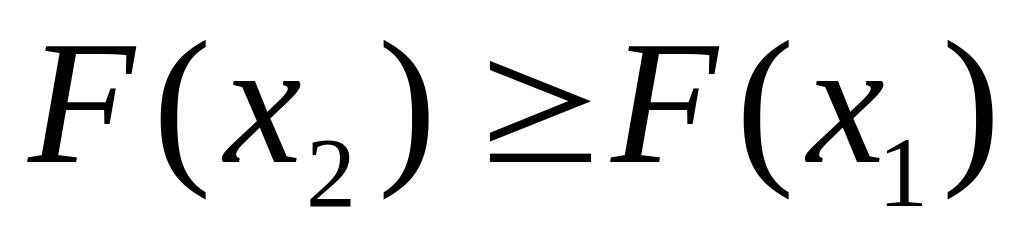, теңсіздігі орындалады.

Салдар 1: Х кездейсоқ шамасы (a,в) аралығында жататын мәндерді қабылдау ықтималдығы таралу функциясының осы аралықтағы өсімшесіне тең, яғни

(6)

Мысал 10: Х кездейсоқ шамасының таралу функциясы

Сынау нәтижесінде Х –тің (0;2) аралығында жататын мәндерді қабылдау ықтималдығын табу керек.

Шешуі: (0;2) интервалында шарт бойынша , онда . Олай болса,

Салдар 2: Үздіксіз Х кездейсоқ шамасының анықталған бір ғана мәнге ие болу ықтималдығы 0-ге тең.

Салдар 3: Егер кездейсоқ шаманың мүмкін мәндері (а; в) аралығында жатса, онда

1) , егер х≤ а ;

2) егер

Келесі шектік қатынастар орындалады :

; .

Таралу функциясының графигі

Таралу функциясының графигі у=0, у=1(1-ші қасиеті) түзүлерімен шектелген жолақта орналасқан. X (a; b) интервалында өскенде, кездейсоқ шаманың барлық мүмкін мәндерінің графигi ‘’жо¹ары к¼терiледi’’. Егер болñà, графиктің ординатасы 0-ге тең; егер болса, графиктің ординатасы 1-ге тең.

F(x)

a 0 b

1 сурет.

11-мысал: Х дискретті кездейсоқ шамасы таралу кестесімен берілсін:

Х	1	4	8
Р	0,3	0,1	0,6

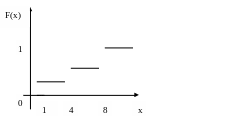
Таралу функциясын табыңыз және графигін салыңыз.

Шешуі: Таралу функциясы аналитикалық түрде былай жазылады.

Үздіксіз кездейсоқ шаманың ықтималдықтарының таралу тығыздығы

Анықтама: Х кездейсоқ шамасының таралу функциясы F(x)-тің туындысы бар болса, онда F(x) туындысын Х шамасының ықтималдықтар таралу тығыздығы деп атайды және оны былай белгілейді: .

Таралу тығыздығы үшін таралу функциясы алғашқы функция болып табылады.

Теорема: Х кездейсоº шамасыны» (à,â) интервалында¹ы м¸нге ие болу ыºтималды¹ы шектерi à-äàí â-¹а дейiнгi алын¹ан таралу ты¹ызды¹ыны» аныºтал¹ан интегралына те»:

12-мысалы: Х кездейсоқ шамасының тығыздығы берілген:

Т¸жiрибе н¸тижесiнде Х шамасы (0,5;1) аралығында жататын мәндерді қабылдау ыºтималды¹ын табы»ыз.

Шешуі: Ізделінді ықтималдық: