Тема 9. Индексы динамики

Индексы

Относительные величины получаемые путем сравнения одноименных показателей во времени или в пространстве в практике экономических исследований и сравнений, часто называют индексами, индексами также называют относительные  величины, характеризующие соотношения показателей в пространстве, времени или темпах изменений экономических показателей, которые представляют практический интерес.

С помощью индексов можно определить количественные изменения самых различных показателей функционирования народного хозяйства, развития социально-экономических процессов и т.п.

В экономической работе с помощью индексов можно объективно и точно показать изменения в росте или снижении производства, изменения в урожайности, состоянии себестоимости и цен выпускаемой продукции, численности работающих, производительности труда, заработной платы, изменения в цене акций на фондовых рынках (индекс Доу Джонса), сравнительная характеристика изменения погоды за определенный период времени (температуры, влажности, давления) и т.д. и т.п.

Индексы в своей основе представляют разновидность относительных величин, характеризующих средние показатели исследуемых процессов или явлений в социально-экономических и других областях деятельности общества. Однако от средних величин, , индексы отличаются тем, что они воплощают в себе, как правило, сводные, обобщающие показатели, т.е. выражают собой некоторое содержание свойственное всем рассматриваемым явлениям и процессам.

Например, предприятие, выпускающее многообразную продукцию, нельзя оценить путем сравнения изменения объемов производства с помощью простого сложения единиц выпускаемой продукции. Необходим какой-то общий измеритель, таким измерителем становится стоимость или себестоимость.

При всем разнообразии индексы можно подразделить на две группы. Одни показатели выражаются абсолютными величинами свойственными всем единицам статистической совокупности. Другие представляют собой показатели, рассчитанные на какую-то единицу (показатели цен, себестоимости, производительности труда, заработной платы и т.п.). Условно первая группа показателей называется количественными и вторая группа условно называется качественными показателями.

-q- количество (объем) товара в натуральном выражении

-p цена единицы товара

-z себестоимость единицы продукции

-w выработка продукции в стоимостном выражении на одного рабочего или в единицу времени

-v выработка продукции в натуральном выражении на одного рабочего или в единицу времени

-T общие затраты времени (tq) или численность рабочих

-pq стоимость продукции или товарооборот

-zq издержки производства

Классификация индексов:

1. по сложности: индивидуальные и агрегатные (простые взвешенные);

2. по характеру базы: с постоянной базой (базовые) и с переменной базой (цепные);

3.по характеру весов: с постоянными весами и с переменными весами (оценивающие влияние индексируемого показателя весов и. оценивающие влияние структурных сдвигов (весов));

4. по виду индексируемого показателя (индекс цен, физического объема, себестоимости, товарооборота и.т.д.)

5. по сфере использования (для анализа АХД и биржевые)

Индексы качественных показателей, которые рассчитываются на физическую единицу (цены, себестоимость, теплотворность единицы энергоресурса и т.д.), определяется в форме единичных показателей, а также в форме общих (групповых) индексов, характеризующих изменения индексируемого показателя в целом по избранной совокупности статистических данных.

Индивидуальные индексы: характеризуют изменение отдельных единиц совокупности

Чтобы различать, к какому периоду относятся индексируемые величины, принято возле символа внизу ставить знаки: "1" - для сравниваемых (отчетных) периодов и "0" - для тех периодов, с которыми производится сравнение (базисных). Например, при сравнении продукции произведенной в 2008 г. с продукцией 2009 г., то объем продукции в 2009 г. условно обозначают через q₁, а продукции 2008 г. - q₀, а соответствующий индивидуальный индекс динамики объема производства будет i_q=q1 / q0;

индивидуальный индекс динамики себестоимости единицы продукции i_z=z₁/z₀; индивидуальный индекс динамики производительности труда по выработке i_B=B₁/B₀ и по трудоемкости и i_t=t₁/t₀.; индивидуальный индекс динамики фондоотдачи i_ф=ф₁/ф₀; индивидуальный индекс выполнения планового задания .

Если рассчитывается индекс для нескольких периодов, то по существующим правилам обозначение, у каждой индексируемой величины, отнесенной к тому или иному периоду, ставится соответствующий знак.

Например, данные о количестве произведенной продукции за 5 лет следует обозначить как q1, q2, q3, q4, q5 и в соответствии с этим рассчитывать предлагаемые индексы как базисные или цепные. Их отличие состоит в том, что за базовый нулевой показатель в одном случае берется предыдущий показатель (x_t-1), а в другом фиксированный (x₀).

Агрегатные индексы обозначаются символом J ; в числителе и знаменателе содержаться соединенные наборы (агрегаты) элементов изучаемой совокупности. Числитель и знаменатель агрегатного индекса представляет собой сумму произведений двух величин, одна из которых меняется (индексируемая величина), а другая остается неизменной и в числителе и в знаменателе(вес индекса).

Наиболее типичным индексом количественного показателя является индекс объема, т.е. индекс физического объема продукции. Допустим, нам необходимо оценить изменения в производстве продукции определенного предприятия или группы предприятий за определенный период времени. Рассматриваемые предприятия производят разнообразную, т.е. несопоставимую по потребительским свойствам продукцию.

Неоднородную продукцию необходимо соизмерить с помощью общих единиц измерения, после чего определить общий объем проданной продукции в отчетном и базисном периодах, найти их соотношение. Для достижения сопоставимости разнородных единиц вводится специальные сомножители индексируемых величин. В качестве такого соизмерителя в практике наших дней используют цену единицы продукции, с помощью чего измеряется объем произведенной несоизмеримой по физическим свойствам продукции.

Индекс физического объема продукции показывает во сколько раз возросла (уменьшилась) стоимость продукции из-за роста (снижения) объемов производства.

Если вычислить разность числителя и знаменателя , то итог (в абсолютных единицах) покажет, на сколько рублей изменилась стоимость продукции в результате изменения объемов производства.

Предположим, стоимость продукции определенного предприятия в базисном периоде (p₀q₀) 2007 г. составляла 125.000 рублей, а стоимость продукции, произведенной в отчетном периоде p₀q₁ (2008 г.) составила 155.000 рублей, то общий индекс физического объема будет представлен в следующем виде: 155000/125000=1,24 т.е. общий выпуск продукции в отчетном периоде по сравнению с базисным увеличился на 24%.

Вычитая из числителя индекса знаменатель, получим 155.000 - 125.000 = 30.000 руб. Полученные числовые данные свидетельствуют о том, что за счет увеличения объема производства на 24% стоимость продукции в абсолютном выражении в отчетном периоде увеличилась на 30.000 рублей.

Индекс стоимости продукции или товарооборота : показывает, во сколько раз возросла стоимость продукции (товарооборота) по сравнению с базисным периодом. Разность числителя и знаменателя , покажет, на сколько рублей изменилась стоимость продукции (товарооборот) в текущем периоде по сравнению с базисным.

Индекс цен – индекс качественного показателя. Индексируемая величина –цена, в качестве веса берется количество товаров отчетного периода. , числитель –стоимость товара в отчетном периоде, знаменатель – условная стоимость того же количества товаров, но по ценам базисного периода. Индекс цен показывает во сколько раз уменьшилась стоимость продукции из-за изменения цен. Разность числителя и знаменателя , покажет, на сколько рублей изменилась стоимость продукции в результате роста (снижения) цен в текущем периоде по сравнению с базисным. Изменение физических объемов не имеет значение.

По статистическим данным полученным в результате определения агрегатного индекса цен мы имеем дополнительную экономическую информацию, а именно: во-первых, вычитая из числителя формулы знаменатель можно определить сумму прибыли или убытка, которую получает продавец от реализации отчетного периода за счет повышения или снижения цен.

Во-вторых, если товарооборот (стоимость) определяется как произведение цены на количество произведенных единиц товара, то и произведение индекса цен на индекс объема должно давать индекс стоимости (товарооборота), т.е. Указанная ранее схема определения агрегатных индексов может использоваться при расчете различных аналитических индексов: индекс издержек производства ; индекс затрат времени на производство продукции:

Индексы структурных сдвигов

Под изменением структуры явления понимается изменение доли отдельных групп единиц совокупности в общей их численности.

Агрегатный индекс цен рассчитанный на основе неизменного объема произведенной продукции (данные отчетного периода) является индексом фиксированного состава - этот индекс называется индексом Пааше.

Индекс структурных сдвигов показывает влияние структурных изменений на динамику средней цены. Он рассчитывается по формуле:

Индекс переменного состава отражает изменение не только индексируемой величины (в данном случае цена), но влияние структуры совокупности (весов).

Между этими индексами существует следующая взаимосвязь:

Средние индексы

Используются в том случае, когда нет возможности рассчитать общий агрегатный индекс, т.е существует недостаток в данных, тогда подставляют индивидуальный индекс среднеарифметический индекс: цен - , среднегармонический индекс цен – ,

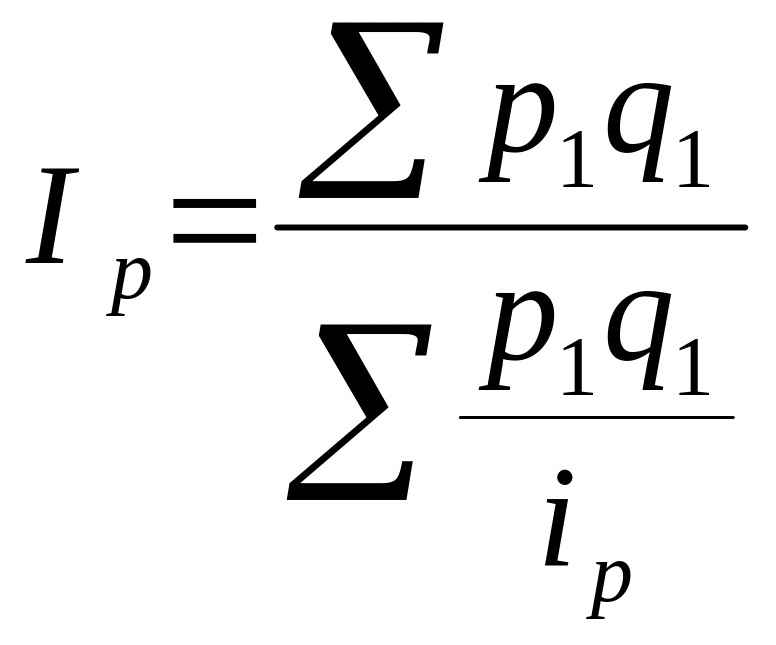Цепные и базисные индексы

Система базисных индексов –это ряд последовательно вычисленных индексов одного и того же явления с постоянной базой сравнения, т.е. в знаменателе всех индексов находится индексируемая величина базисного периода ; ; … - индекс стоимости, базисные индексы цен - ; ; … - это индексы с переменными весами.

Базисные индексы цен с постоянными весами - - ; ; …

Система цепных индексов – это ряд индексов одного и того же явления, вычисленные с меняющейся от индекса к индексу базой сравнения - ; ; … , цепной индекс стоимости, цепной индекс цен ; ; …

Цепные индексы цен с постоянными весами ; ; …

ВОПРОСЫ

Пример

Пример1. Рассчитать индивидуальные и общие индексы товарооборота, физического объема проданных товаров и цен по следующим данным о ценах и реализации (товаров) за два месяца: Таблица 14

То вары	Январь			Февраль			Индексы (%)
	Цена, руб.	Реализация		Цена, руб	Реализация		Цен	Физического объема продаж	Товарооборота
		кг	руб.		кг	руб.
	1	2	3	4	5	6	7	8	9
А	10	800	8000	8	750	6000	80	93	75
Б	5	400	2000	5	540	2700	100	135	135
В	2	150	300	3	200	600	150	150	200
Итого	-	-	10300	-	-	9300	87.5	102.7	90.3

Индивидуальные индексы, характеризующие динамику показателей по каждому товару, помещены в графах 7, 8, 9 таблицы по строкам А, Б, В. Они легко получаются путем сравнения соответствующих показателей за январь и февраль (например, индекс цен по товару "А" равен . Сводные индексы записаны по итоговой строке этих колонок. Они рассчитаны следующим образом: Полученный результат указывает на то, что цены снизились на 12.3%.

Из формулы следует, что индекс цен есть отношение стоимости товаров отчетного периода к стоимости тех же товаров, но по базисным (у нас январским) ценам. Снижение цен привело к удешевлению массы товаров, проданных в феврале в абсолютном выражении на сумму 1300 руб. (10600-9300).

Индекс количества проданных товаров (физического объема товарооборота) рассчитывается как отношение товарооборота отчетного периода по базисным ценам к товарообороту базисного периода:

Следовательно, физический объем продажи возрос на 2,7%.

Индекс товарооборота (стоимости проданных товаров) может быть получен двумя способами:

1 ) по формуле

2) на основе рассчитанных индексов

Если индексы рассчитываются за три и более периодов, то в зависимости от задач исследования и имеющихся данных выбирают один из четырех возможных вариантов построения индексной системы: цепные индексы с переменными или постоянными весами, базисные индексы с переменными или постоянными весами.

Для изучения динамики среднего уровня в статистике используют систему взаимосвязанных индексов, которая включает в себя индекс переменного состава, индекс фиксированного (постоянного) состава, индекс структурных сдвигов. Данные индексы позволяют определить, как изменится средняя величина за счет изменения индивидуальных значений признака и за счет изменения структуры производства или реализации.

Индекс переменного состава определяется по формуле

Данный индекс показывает как изменится средняя цена за счет изменения цен и структуры совокупности.

Индекс фиксированного состава показывает только изменение цен и рассчитывается по формуле:

Индекс структурных сдвигов показывает влияние структурных изменений на динамику средней цены. Он рассчитывается по формуле:

Между этими индексами существует следующая взаимосвязь:

Рассмотрим расчет этих индексов на примере.

Пример 2. По нижеследующим данным определим общий индекс цен на товар "А" в двух формах: фиксированного и переменного состава, а также оценим влияние структурных сдвигов на динамику средней цены:

Таблица 15

Рынки	Цена за 1 кг товара (руб.)		Продано товара (кг)
	I кв.	II кв.	I кв.	II кв.
N1	15	12	500	300
N2	10	10	500	700

Индекс цен переменного состава получается как отношение средней цены двух сравниваемых периодов:

Таким образом, средняя цена товара на двух рынках снизилась на 15,2% во II квартале по сравнению с I кварталом за счет снижения цен и изменения в структуре реализации.

Индекс цен фиксированного состава рассчитаем по уже известной формуле:

Таким образом, цена товара на двух рынках снизилась на 7,9% во II квартале по сравнению с I кварталом.

Средняя цена товара снизилась на 8% во II квартале по сравнению с I кварталом за счет изменения структуры реализации. Проверим взаимосвязь:

3. пример использования средних индексов

Товар	Реализация в текущем периоде, руб.	Изменение цен в текущем периоде по сравнению с базисным,%	Расчетные графы
Морковь Свекла лук	23000 21000 29000	+4,0 +2,3 -0,8	1,040 1,023 0,992	22115 20528 29234
	73000	-	-	71877

или 101,6% Цены по данной товарной группе в текущем периоде по сравнению с базисным в среднем возросли на 1,6%.