Часть I: линейная задача оптимизации и ее приложения.

Глава I. Задача линейного программирования.

I. 4. Основные утвержднеия теории двойственности и их экономическое содержание.

I. 4.1. Первая теорема двойственности.

Здесь, в первую очередь, по структуре прямой и двойственной задач (в их канонической постановке), важно отметить, что для любых допустимых планов и (каждой из пары взаимодвойственных задач) справедливо неравенство

С экономической точки зрения, это означает, что для любого допустимого плана производства и любого допустимого вектора оценок ресурсов общая созданная стоимость не превосходит суммарной оценки ресурсов.

Очевидно, что можно найти такие допустимые и пары двойственных по отношению друг к другу задач, для которых выполняется соотношение В этом случае и - оптимальные планы соответствующих задач. Это утверждение - достаточный признак оптимальности, носит название критерия оптимальности Канторовича. Его экономический смысл следующий: план производства и вектор оценок ресурсов являются оптимальными, если цена всей произведенной продукции и суммарная оценка ресурсов совпадают.

Заметим, что для существования оптимального плана любой из пары двойственных задач необходимо и достаточно существование дополнительного плана для каждой из них.

Теорема (первая теорема двойственности): если одна из двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем соответствующие экстремальные значения целевых функций совпадают: Если одна из двойственных задач неразрешима в следствие неограниченности целевой функции на множестве допустимых решений, то система ограничений другой задачи противоречива.

Таким образом, если задача определения оптимального плана, максимизирующей выпуск продукции, разрешима, то разрешима и задача определения оценок ресурсов. Причем цена продукта, совпадает с суммарной оценкой ресурсов. Совпадения значений целевых функций для соответствующих решений пары двойственных задач достаточно для того, чтобы эти решения были оптимальными. Это значит, что план производства и вектор оценок ресурсов являются оптимальными тогда и только тогда, когда цена произведенной продукции и суммарная оценка ресурсов совпадают. Оценки выступают как инструмент балансирования затрат и результатов. Двойственные оценки обладают тем свойством, что они гарантируют рентабельность оптимального плана, то есть равенства общей оценки продукции и ресурсов; обуславливает убыточность всякого другого плана, отличного от оптимального. Двойственные оценки позволяют сопоставлять и балансировать затраты и результаты системы.

Напомним, что как уже было отмечено ранее, связь между задачами двойственной пары глубже, нежели указано в формулировке теоремы: решая симплекс-методом одну из них, автоматически получается решение второй задачи.

I. 4.2. Вторая теорема двойственности и ее экономическое содержание.

Здесь мы сразу приведем формулировку этой теоремы.

Теорема (о дополняющей нежесткости): для того, чтобы планы и пары двойственных задач были оптимальными, необходимо и достаточно выполнение условий:

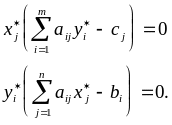
Это условия дополняющей нежесткости. Из них следует: если какое-либо неравенство системы ограничений одной из задач не обращается в тождество оптимальным планом этой задачи, то соответствующая компонента оптимального плана двойственной задачи должна равняться нулю; если же какая-либо компонента оптимального плана одной из задач положительна, то соответствующее ограничение в двойственной задаче ее оптимальным планом должно обращаться в тождество, то есть, если:

то если то

Точно так же, если:

то если то

Экономически это можно интерпретировать следующим образом. Если по некоторому оптимальному плану производства, расход го ресурса строго меньше его запасов , то в оптимальном плане соответствующая двойственная оценка единицы этого ресурса равна нулю. Если в некотором оптимальном плане оценок его я компонента строго больше нуля, то в оптимальном плане производства расход соответствующего ресурса равен его запасу.

Отсюда следует вывод: двойственные оценки могут служить мерой дефицитности ресурсов. Дефицитный ресурс (полностью используемый по оптимальному плану производства) имеет положительную оценку, а избыточный ресурс (используемый не полностью) имеет нулевую оценку.

ПРИМЕР: Продукция в цехе может производиться тремя технологическими способами Объемы ресурсов и их расход в единицу времени для каждой технологии, а также производительности (эффективности) технологий (в денежных единицах за единицу времени работы по данной технологии) представлены в таблице данных.

Определим оптимальный план использования каждого технологического способа , то есть время использования каждого технологического способа (запишем решение двойственной задачи и проверим условия о дополняющей нежесткости).

Таблица данных

Ресурсы	Технологические способы			Объем ресурса
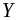
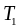
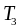
Рабочая сила (чел.-ч.)	15	20	25	1200
Сырье (т)	2	3	2,5	150
Электроэнергия (кВт.ч)	35	60	60	3000
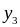
Производительность технологического способа	300	250	450
План

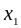
ПРЯМАЯ ЗАДАЧА

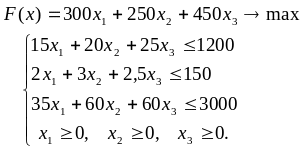
ДВОЙСТВЕННАЯ ЗАДАЧА