Основы молекулярной физики и термодинамики

Два подхода различны, но взаимно дополняют друг друга.

Молекулярная (статистическая) физика использует математический аппарат теории вероятностей и представляет процессы, происходящие в телах как результат осредненного движения атомов и молекул.

Термодинамика основана на общих принципах (началах), которые являются обобщением опытных фактов и используются для описания состояния термодинамической системы в условиях равновесия и процессов перехода из одного состояния в другое.

Молекулярно-кинетическая теория идеальных газов (мкт)

Основное уравнение молекулярно-кинетической теории идеальных газов

В молекулярно-кинетической теории (МКТ) используют модель идеального газа, которая удовлетворяет следующим условиям:

собственный объем молекул газа мал по сравнению с занимаемым этим газом объемом (молекулы –материальные точки);

между молекулами газа отсутствуют силы взаимодействия;

столкновения молекул газа между собой и со стенками абсолютно упругие.

Основное уравнение МКТ связывает параметры состояния газа: давление Р, объем V и абсолютную температуру Т с осредненными характеристиками движения его молекул, т. е. со средней квадратичной скоростью и средней кинетической энергией молекул .

Для вывода основного уравнения МКТ рассмотрим одноатомный идеальный газ, молекулы которого движутся с постоянной скоростью , а число столкновений между ними малό по сравнению с числом ударов о стенки сосуда (столкновения абсолютно упругие). Хаотическое движение молекул, для которых равновероятны все направления, заменим движением вдоль трех взаимно-перпендикулярных осей x, y, z.

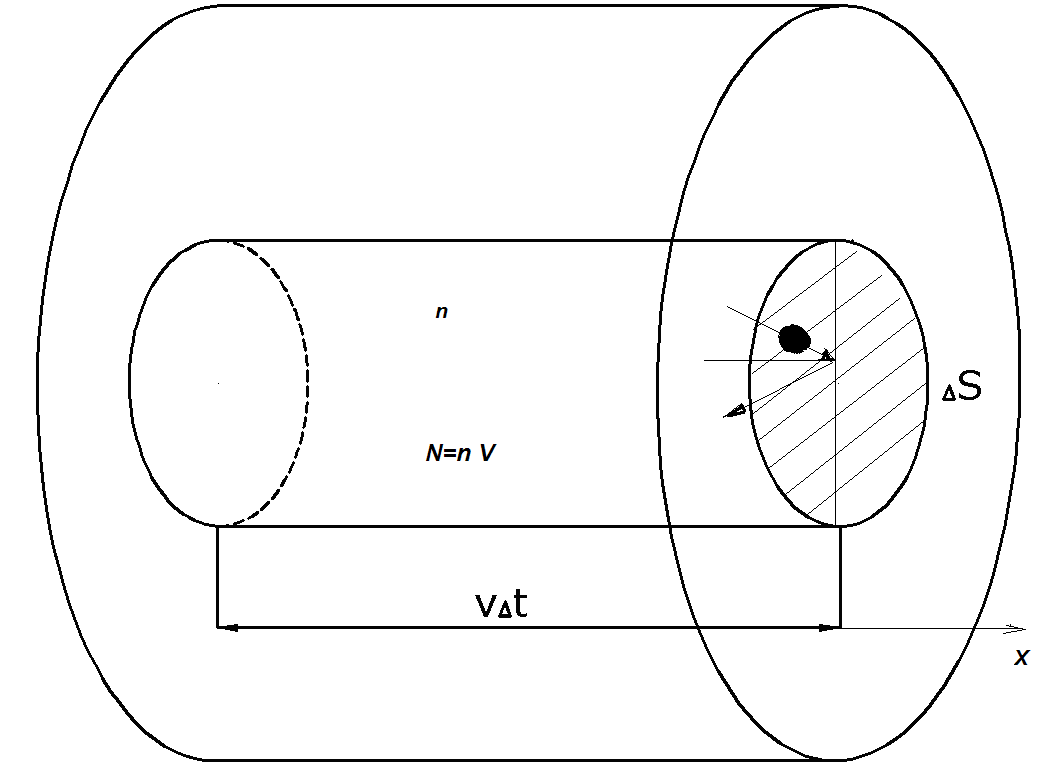
Выделим на стенке сосуда элементарную площадку s и рассчитаем давление, которое оказывает на нее идеальный газ.

При каждом соударении молекула массой m_о передает стенке импульс

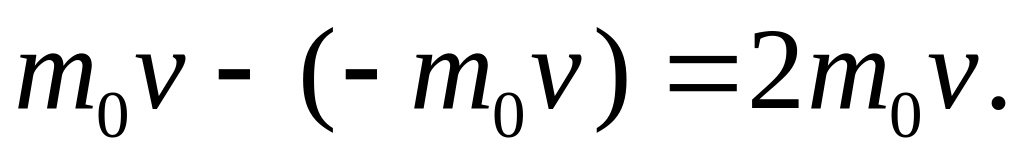
За время выделенной площадки могут достигнуть только те молекулы, которые заключены в объеме цилиндра с основанием и высотой . Если принять, что n – концентрация молекул, т. е. количество молекул в единице объема, то общее число молекул, находящихся в объеме цилиндра, можно представить как

в любой момент времени вдоль оси x движется 1/3 всех молекул (1/3 N), находящихся в объеме выделенного цилиндра, а к рассматриваемой площадке – 1/6 N, так как два направления равновероятны.

Следовательно, о площадку ударится 1/6 N или

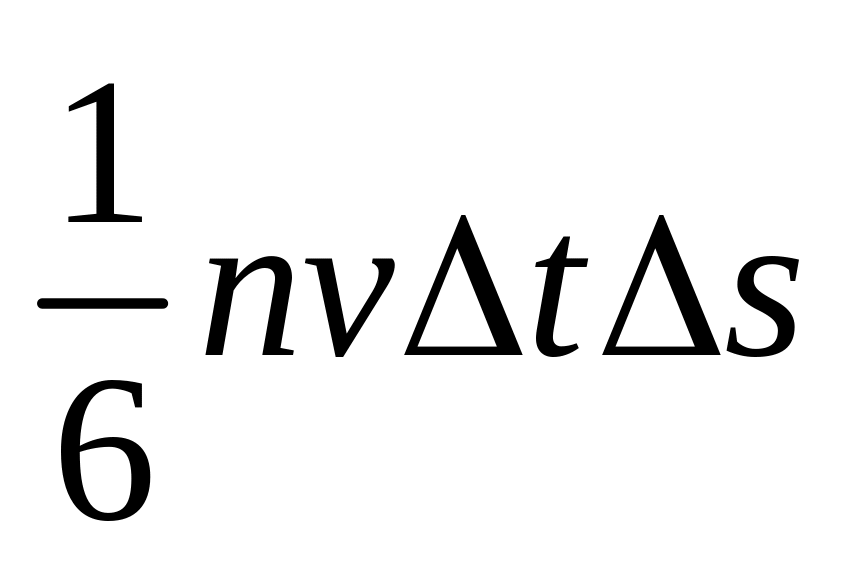молекул, которые передадут ей импульс

.

По второму закону Ньютона

.

Давление Р, оказываемое на площадку, определится как

При выводе уравнения предполагалось, что скорости молекул одинаковы, однако, они двигаются с разными скоростями v₁, v₂, ... v_n. Таким образом, всю совокупность молекул N характеризует средняя квадратичная скорость , которая определяется как

.

С учетом этого давление

или

основное уравнение МКТ.

Связь термодинамической характеристики газа, его температуры T, с осредненной кинетической энергией теплового движения молекул была установлена Больцманом и имеет вид

где k – постоянная Больцмана, равная

При Т = 0 средняя кинетическая энергия теплового движения молекул , т. е. должно прекратиться тепловое движение молекул.

Из основного уравнения МКТ следует, что

т. е. давление идеального газа прямо пропорционально концентрации его молекул и температуре газа.