§ 5. Необходимый признак экстремума.

Установим признак, дающий необходимое условие того, чтобы данная точка являлась точкой экстремума.

Необходимый признак экстремума (1.5).

В точке экстремума дифференцируемой функции ее производная либо равна нулю, либо не существует.

1.5. Необходимый признак экстремума (адрес файла Блок 4 ___ ). В точке экстремума дифференцируемой функции ее производная либо равна нулю, либо не существует. Вернитесь к тексту

Доказательство.

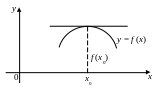
Пусть функция у = f (х) имеет в точке х = х₀ максимум. Тогда значение f (х₀)  f (х), где х из окрестности точки х₀. При доказательстве теоремы Ролля (9.2 ПМ. ДИФОП–9) отметили, что в тех внутренних точках интервала, в которых дифференцируемая функция достигает своего наибольшего значения, производная f (х) = 0. Следовательно, f (х₀) = 0. Аналогично доказывается для минимума функции.

Геометрически условие f (х₀) = 0 обозначает, что в точке экстремума дифференцируемой функции f (х) касательная к ее графику параллельна оси Ох (рис. 6).

Рис. 6.

Замечание. Функция может иметь экстремумы и в тех точках, в которых она не дифференцируема. Например, показано на Рис. 7.

Рис. 7.

Точки М₁ и М₂ называются точками возврата функции.

Значения аргумента, при которых производная либо равна нулю, либо не существует, называются критическими или стационарными точками функции.

§ 6. Достаточные признаки экстремума.

Для того чтобы иметь возможность судить о том, когда же данная точка будет являться точкой экстремума, надо установить достаточный признак экстремума. Таких признаков два.

Первый достаточный признак экстремума (1.6).

Точка х₀ является точкой экстремума дифференцируемой функции f (х), если при переходе аргумента х слева направо через критическую точку х₀ производная f (х) меняет знак; при перемене знака «+» на «» точка х₀ является точкой максимума; при перемене «» на «+» точка х₀ является точкой минимума.

Доказательство.

Пусть при переходе х через х₀ производная меняет знак с «+» на «». Это значит, что слева от х₀ находится какой-либо интервал возрастания функции, а справа – какой-либо интервал убывания. Следовательно, точка х₀ – точка максимума функции.

Так же убеждаемся, что при перемене знака производной с «» на «+» точка х₀ есть точка минимума функции.

Пример. Исследовать функцию на экстремум у = 2х³  6х²  18х + 7.

Решение. Область определения функции D (у) = (; +). Найдем критические точки функции.

у = 6х²  12х  18; у = 0; 6х²  12х  18 = 0;

х²  2х  3 = 0, х₁ = 1, х₂ = 3 (по теореме Виета)

х = 1  D (у), х = 3  D (у).

(; 1): у  0, у 

(1; 3): у  0, у 

(3; +): у  0, у 

Числовую ось критическими точками разбили на три интервала, определили знак у в каждом из интервалов. По достаточному признаку экстремума видим, что в точке х = 1 функция имеет максимум, а в точке х = 3  минимум. Находим значения функции в каждой из этих точек.

у (1) = 17, у (3) = 47.

Ответ: (1; 17)  max y; (3; 47)  min y.

Второй достаточный признак экстремума (1.6).

Точка х₀ есть точка экстремума функции f (х), если f (х₀) = 0, а f (х₀)  0, причем, если

f (х₀)  0, то х₀  точка минимума, а если f (х₀)  0, то х₀  точка максимума.

1.6. Первый достаточный признак экстремума (адрес файла Блок 4 ___ ). Точка х0 является точкой экстремума дифференцируемой функции f (х), если при переходе аргумента х слева направо через критическую точку х0 производная f (х) меняет знак; при перемене знака «+» на «» точка х0 является точкой максимума; при перемене «» на «+» точка х0 является точкой минимума. Второй достаточный признак экстремума. Точка х0 есть точка экстремума функции f (х), если f  (х0) = 0, а f  (х0)  0, причем, если f  (х0)  0, то х0  точка минимума, а если f  (х0)  0, то х0  точка максимума. Вернитесь к тексту

Доказательство.

Пусть f  (х₀) = 0, а f  (х₀)  0. Предполагая вторую производную непрерывной, можно считать, что она сохраняет свой знак в некоторой окрестности точки х₀. Отсюда следует, что функция f  (х) (от нее взята вторая производная) в этой окрестности будет возрастающей, т.к.

f  (х₀)  0. Так как f  (х₀) = 0, то слева от точки х₀ производная f  (х), принимая меньшие значения, будет отрицательной: f  (х)  0, а справа – принимая большие значения,  положительной:

f  (х)  0. Это значит, что функция f  (х) при переходе аргумента х слева направо через точку х₀ меняет свой знак с «» на «+». По первому достаточному признаку экстремума точка х₀ является точкой минимума.

Рассуждая аналогично, получим, что если f  (х₀)  0, то f  (х) убывает и при переходе аргумента х через точку х₀ меняет знак с «+» на «», т.е. точка х₀ есть точка максимума.

Замечание. В том случае, когда f  (х₀) = 0 и f  (х₀) = 0, а также в случае, когда первой производной не существует, вторым признаком воспользоваться нельзя. Нужно пользоваться первым достаточным признаком.

Пример. Исследовать функцию на экстремум у = х³  2х² + х.

Решение. Область определения функции D (у) = (; +). Найдем критические точки функции.

у = 3х²  4х + 1, у = 0, 3х²  4х + 1 = 0.

D = 16  12 = 4, .

; х₁ = 1,  критические точки, обе принадлежат D (у).

Найдем вторую производную: у = 6х  4. Подставим х = 1 и в у.

у (1) = 6  4 = 2  0,

.

Найдем значения функции у в точках х = 1, .

у (1) = 1  2 + 1 = 0,

.

(1; 0)  min f (х),

 max f (х).