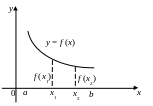ПМ. ИФПП – 1. ВОЗРАСТАНИЕ И УБЫВАНИЕ ФУНКЦИИ. УСЛОВИЯ ВОЗРАСТАНИЯ И УБЫВАНИЯ ФУНКЦИЙ ЭКСТРЕМУМЫ ФУНКЦИЙ. НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМА ФУНКЦИИ. НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ ФУНКЦИИ НА ОТРЕЗКЕ.

ПМ. ИФПП – 1. Ключевые слова и понятия.

1. Возрастание и убывание функции.

2. Необходимый признак возрастания и убывания функции.

3. Достаточный признак возрастания и убывания функции.

4. Максимум и минимум функции.

5. Необходимый признак экстремума.

6. Достаточные признаки экстремума.

7. Правило нахождения наибольшего и наименьшего значения функции на отрезке.

1.1. Входная информация для самопроверки.

Приступая к изучению данной темы, Вам необходимо восстановить в памяти (или восполнить) знания из прошлых периодов обучения:

• из курса средней школы: теорема Виета, формула корней квадратного уравнения, решение неполных квадратных уравнений, метод интервалов, область определения функции;

• из курса прикладной математики: определения приращения аргумента (9.2 ПМ – МА. 9), приращения функции (9.2 ПМ – МА. 9), определение производной (1.2 ПМ. ДИФОП–1), геометрический смысл производной (1.2 ПМ. ДИФОП–1), производная ІІ порядка (7.6 ПМ. ДИФОП – 7), правило дифференцирования алгебраической суммы (1.7 ПМ. ДИФОП–1), правило дифференцирования произведения (1.8 ПМ. ДИФОП–1) ,правило дифференцирования частного(1.9 ПМ. ДИФОП–1), теорема Ролля (9.2 ПМ. ДИФОП–9), теорема Лагранжа (9.3 ПМ. ДИФОП–9).

1.2. Содержание темы

1.2.1. Структурно-логическая схема содержания темы

1.2.2. Тематическое содержание.

§ 1. Возрастание и убывание функции на интервале.

Дана функция у = f (х) на интервале (а; b). Дадим определения возрастающей и убывающей функции на интервале (а; b).

Возрастание и убывание функции на интервале (1.1).

Функция у = f (х) называется возрастающей на интервале (а; b), если для любых двух значений ее аргумента х₁ и х₂ из интервала (а; b) таких, что х₂  х₁, выполняется неравенство

f (х₂)  f (х₁).

1.1. Возрастание и убывание функции на интервале (адрес файла Блок 4 ___ ). Функция у = f (х) называется возрастающей на интервале (а; b), если для любых двух значений ее аргумента х1 и х2 из интервала (а; b) таких, что х2  х1, выполняется неравенство f (х2)  f (х1). Вернитесь к тексту

Функция у = f (х) называется убывающей на интервале (а; b), если для любых двух значений ее аргумента х₁ и х₂ из интервала (а; b) таких, что х₂  х₁, выполняется неравенство

f (х₂)  f (х₁).

1.2. Возрастание и убывание функции на интервале (адрес файла Блок 4 ___ ). Функция у = f (х) называется убывающей на интервале (а; b), если для любых двух значений ее аргумента х1 и х2 из интервала (а; b) таких, что х2  х1, выполняется неравенство f (х2)  f (х1). Вернитесь к тексту

Графически это выглядит так: Рис. 1., 2.

х2  х1 f (x2)  f (x1) Рис. 1.

х2  х1 f (x2)  f (x1) Рис. 2.

Функцию, возрастающую или убывающую на интервале, называют монотонной функцией.

§ 2. Необходимый признак возрастания и убывания функции.

Для исследования функции на возрастание или убывание используют необходимый признак возрастания или убывания функции (необходимый признак монотонности функции).

Необходимый признак возрастания и убывания функции (1.2).

1. Если дифференцируемая функция у = f (х) возрастает на интервале, то производная этой функции f  (х) неотрицательна на этом интервале.

2. Если дифференцируемая функция у = f (х) убывает на интервале, то производная этой функции f  (х) неположительная на этом интервале.

1.2. Необходимый признак возрастания и убывания функции (адрес файла Блок 4 __ ). Если дифференцируемая функция у = f (х) возрастает на интервале, то производная этой функции f  (х) неотрицательна на этом интервале. Если дифференцируемая функция у = f (х) убывает на интервале, то производная этой функции f  (х) неположительная на этом интервале. Вернитесь к тексту

Доказательство.

1. Пусть дифференцируемая функция f (х) возрастает на интервале (а; b). По определению производной функции

.

Пусть х и х +  х принадлежат (а; b).

f (х +  х)  f (х) для  х  0, f (х +  х)  f (х)  0;

f (х +  х)  f (х) для  х  0, f (х +  х)  f (х)  0.

В обоих случаях

.

Следовательно, производная f  (х)  0.

2. Пусть функция f (х) убывает на (а; b). Тогда,

f (х +  х)  f (х) для  х  0, f (х +  х)  f (х)  0;

f (х +  х)  f (х) для  х  0, f (х +  х)  f (х)  0.

В обоих случаях

.

Производная

.

Замечание. Геометрически утверждение теоремы сводится к тому, что для графика возрастающей дифференцируемой функции касательные образуют с положительным направлением оси Ох острые углы (tg  = f  (x)) или в некоторых точках параллельны оси Ох.

Для графика убывающей дифференцируемой функции все касательные образуют тупые углы с положительным направлением оси Ох или параллельны ей (рис. 3).

Рис. 3

Таким образом, в интервале монотонности функции знак ее производной не может измениться на обратный.