МДК 04.02 ПР-1

Практическая работа №1

Исследовать индуктивный датчик перемещений, изучить конструкцию и работу, схемы включения и статические характеристики индуктивных датчиков.

Общие сведения:

1 Устройство и принцип действия индуктивного датчика

Простейший индуктивный датчик представляет собой дроссель с переменным воздушным зазором в магнитопроводе. На рис. 6.1 по­казаны две наиболее распространенные конструктивные схемы индуктивных датчиков на одном сердечнике. Это одинарные индуктивные датчики. На сердечнике 1 из электротехнической стали размещена обмотка 2, подключаемая к источнику переменного напряжения. Магнитный поток в сердечнике замыкается через якорь 3, который может перемещаться относительно сердечника 1. Якорь 3 механически связан с деталью, перемещение которой необ­ходимо измерить.

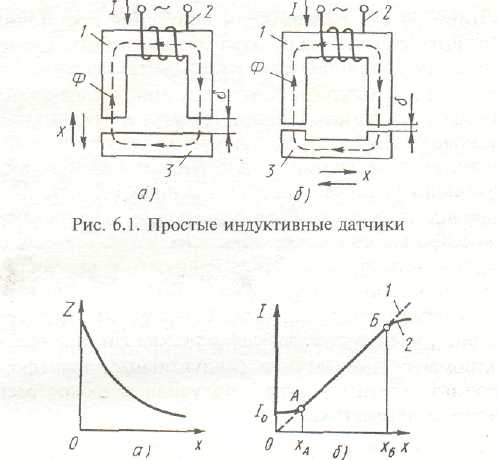
Рисунок 78 Простые индуктивные датчики

Эта деталь на рисунке не показана, но перемещение х ее может происходить в вертикальном направлении. Перемещение якоря изменяет магнитное сопротивление магнитной цепи, состоящей из сердечника, якоря и воздушного зазора δ. Следовательно, изменится индуктивность обмотки 2. Поскольку эта обмотка включена на переменное напряжение, ток в обмотке 2 будет определяться ее полным сопротивлением, в которое входит и индуктивное сопротивление. С увеличением воздушного зазора магнитное сопротивление увеличивается, а индуктивность, индуктивное и полное сопротивления уменьшаются. Следовательно, ток в обмотке увеличива­ется. Полагая ток I в обмотке за выходной сигнал датчика, а перемещение х — за входной сигнал, имеем выходную статическую характеристику в виде графика I=f(х).

2 Вывод уравнения статической характеристики индуктивного датчика

Рисунок 79 Характеристики индуктивного датчика.

Найдем выражение, определяющее зависимость тока в обмотке датчика от перемещения. Анализ проведем применительно к конструктивной схеме, показанной на рисунке 78 а. В этом случае приращение перемещения х всегда равно приращению зазора δ, поэтому нам необходимо получить математическую зависимость тока I от зазора δ: I=f (δ).

Пусть обмотка датчика включена на напряжение питания; u = √2U sin w t, где U — действующее значение напряжения, w — угловая частота, рад/с. По закону Ома, действующее значение тока в обмотке

I=U/z, (32)

где z — полное сопротивление обмотки датчика, Ом, состоящее из активного R и индуктивного X_L сопротивлений:

z = √R² + X_L². (33)

Индуктивное сопротивление X_L пропорционально индуктивности L и частоте питания f:

X_L = 2πfL = w L. (34)

z = √R² + (2πfL)². (35)

Индуктивность обмотки датчика с числом витков w

L = w Ф/ I, (36)

где Ф — магнитный поток сердечника, Вб. Принимаем, что весь магнитный поток проходит через воздушный зазор, т. е. потоки рассеяния отсутствуют. Тогда

Ф = I w /R_м. (37)

Здесь R_м — магнитное сопротивление магнитопровода датчика, Гн^-1. Это сопротивление слагается из сопротивления стали сердечника и якоря R_CT и сопротивления воздушного зазора R_B:

R_м = R_CT + R_B. (38)

Сопротивление воздушного зазора пропорционально удвоенной длине воздушного зазора δ, поскольку магнитный поток проходит через воздушный зазор дважды:

R_B = 2δ/(µ₀s_м), (39)

где s_м — поперечное сечение воздушной части магнитопровода, рав­ное активной площади поперечного сечения сердечника в зоне воздушного зазора, м²; µ₀ = 4π·10^-7 Гн/м — магнитная проницаемость вакуума (магнитная постоянная).

После подстановки (6.5) и (6.6) в (6.4) получим выражение для магнитного потока:

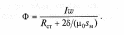(40)

Выражение для индуктивности получаем подстановкой (6.7) в (6.3):

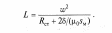(41)

Индуктивное сопротивление обмотки

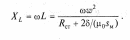(42)

Полное сопротивление обмотки

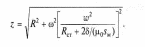(43)

Анализ формулы (43) показывает, что с увеличением воздушного зазора (а следовательно, и перемещения) полное сопротивление уменьшается, стремясь в пределе к величине активного сопро­тивления обмотки R. Ток в обмотке датчика

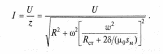(44)