- •Министерство образования и науки Российской федерации
- •Введение
- •Обозначения и символика
- •Греческий алфавит
- •1. Общие указания к оформлению контрольной работы
- •1.1. Рекомендации по оформлению контрольной работы
- •1.2. Общие правила оформления чертежей
- •1.2.1. Форматы (гост 2.301-68*)
- •1.2.2. Основная надпись (гост 2.104-68*)
- •1.2.3. Масштабы (гост 2.302-68*)
- •1.2.4. Линии чертежа (гост 2.303 – 68*)
- •1.2.5. Шрифты чертежные (гост 2.304 – 81*)
- •1.3. Задание контрольную работу №1
- •1.3.1. Задание №1. «Позиционные задачи».
- •1.3.2. Задание №2 «Метрические задачи».
- •2. Позиционные задачи
- •2.1. Пересечения прямой линии с плоскостью
- •2.2. Пересечение двух плоскостей
- •2.3. Пересечение поверхностей
- •2.3.1. Построение линии пересечения поверхностей одна, из которых проецирующая
- •2.3.2. Построение линии пересечения поверхностей методом вспомогательных секущих плоскостей
- •2.3.3. Способ вспомогательных сфер
- •2.4. Контрольные вопросы для подготовки к экзамену
- •Какой чертеж называется комплексным?
- •3. Метрические задачи
- •3.1. Определение расстояния между скрещивающимися прямыми
- •3.2. Определение натуральной величины двугранного угла
- •3.3. Определение расстояния от точки до плоскости
- •3.4. Определение натуральной величины отрезка
- •3.5. Определение натуральной величины плоской геометрической фигуры
- •3.6. Развертки поверхностей
- •3.7. Контрольные вопросы для подготовки к экзамену
- •Литература
- •Содержание
2.3. Пересечение поверхностей
Упражнение № 3. «Пересечение поверхностей»
Построить проекции линии пересечения поверхностей.
Определить видимость линии пересечения и сторон поверхностей относительно друг друга.
Содержание работы. На двух заданных проекциях попарно взаимно пересекающихся поверхностей построить проекции их линий пересечения и определить видимость. М1:1. Задание по вариантам для всех трех задач для удобства расположено в данном сборнике на одном чертеже (таблица 4 приложение 1).
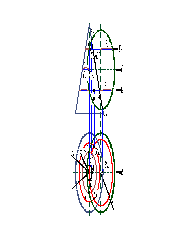
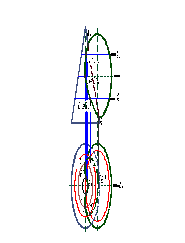
Пример: Построить проекции линии пересечения поверхностей. В качестве центральной поверхности взята поверхность прямого кругового конуса (рис. 16).
В результате получим три задачи:
Задача №1 - построение линии пересечения проецирующей поверхности с поверхностью общего положения.
Задача №2 - построение линии пересечения поверхностей общего положения с параллельными осями (способ вспомогательных секущих плоскостей).
Задача №3 - построение линии пересечения поверхностей вращения общего положения с пересекающимися осями (способ концентрических сфер).
|
Рис. 16 |
2.3.1. Построение линии пересечения поверхностей одна, из которых проецирующая
Если одна или обе заданные поверхности занимают проецирующее положение, то решение задачи упрощается из-за того, что одна из проекций линии пересечения будет совпадать со следом проецирующей поверхности, которая входит в условие задачи. Решение сводится к определению недостающей проекции линии, принадлежащей поверхности, если известна одна ее проекция и указаны проекции поверхности.
Задача 1. Построить проекции линии пересечения поверхности прямого кругового конуса h с поверхностью прямого кругового цилиндра g (рис. 17).
|
|
Рис.17
|
|
Решение:
1. g П2, следовательно фронтальная проекция линии пересечения совпадет с фронтальной проекцией очерка g (g 2).
2. Горизонтальная проекция линии пересечения определяется из условия принадлежности линии поверхности.
2.3.2. Построение линии пересечения поверхностей методом вспомогательных секущих плоскостей
Сущность способа состоит в том, что заданные поверхности пересекают третьей, вспомогательной поверхностью и находят линии, по которым вспомогательная секущая поверхность пересекает каждую из заданных поверхностей.
Построение линий пересечения начинают с определения опорных точек. Опорными называются точки, определяющие особые, характерные свойства линии пересечения и ее проекций. К ним относят:
1) точки, лежащие в общих плоскостях симметрии;
2) точки, лежащие на контурах поверхностей;
3) точки экстремума (крайние верхние, крайние нижние, крайние правые, крайние левые и т.д.) линии пересечения.
Алгоритм решения:

Рис. 18
1. Определяются опорные точки. Это экстремальные точки (удаленные на максимальное и минимальное расстояния от плоскостей проекций) и точки, расположенные на очерковых образующих поверхностей, которые определяют границы видимости проекций кривой.
2. Между опорными точками проводится плоскость-посредник , (рис.18).
3.Строятся линии пересечения проведенной плоскости–посредника с поверхностями – окружности (параллели).
∩ Ψ=m; ∩ Φ = n
4. Определяются точки пересечения построенных параллелей. m∩ n = A-B
5. Проводится еще ряд плоскостей-посредников /, //между опорными точками, и все построения повторяются. Количество плоскостей-посредников зависит от требуемой точности построения линии пересечения.
6. Полученные точки А, В, С и т.д. принадлежат обеим поверхностям одновременно, следовательно, принадлежат искомой линии пересечения. Точки соединяются плавной кривой с учетом их видимости.
Задача 2. Построить проекции линии пересечения поверхностей прямого кругового конуса α с сферы β(рис. 19).
|
|
Рис. 19
Решение:
Шаг 1. В качестве секущих плоскостей используем горизонтальные плоскости уровня, пересекающие обе поверхности по окружностям.
Шаг 2 Построения начинаем с опорных точек, не требующих дополнительных построений для их нахождения. К ним относятся точки А – высшая и В – низшая точки сечения (рис.20), лежащие в плоскости Δ и принадлежащие очерковым образующим конуса и сферы на П2 – А2 и В2. На плоскости проекций П1 – А1 и В1 находим с помощью линии связи. Эти точки устанавливают границы, в которых следует проводить вспомогательные плоскости.
Рис. 20 |
|
Шаг 3. Определим точки С и С′ – точки пересечения экватора сферы с поверхностью конуса. Для этого проведем плоскость Г, которая пересекает сферу по экватору m, конус – по параллели n. Окружности m и n, пересекаясь, определяют горизонтальные проекции точки С1 и С1′. Фронтальные проекции этих точек находятся на фронтальном следе секущей плоскости Г2. Горизонтальные проекции точки С (С1 и С1′) разграничивают горизонтальную проекцию линии пересечения на видимую и невидимую части (рис.21).
|
Рис.22 |
Шаг 4. Промежуточные точки определим с помощью плоскости Σ, которая пересекает сферу по окружности t′, конус – по окружности l′. Пересекаясь, эти окружности дают пару точек D и D′, принадлежащих линии пересечения поверхностей. Количество секущих плоскостей зависит от требуемой точности построения (рис.22).
Шаг 5. Найденные точки соединяем плавной кривой линией c учетом видимости точек. Определяем видимость поверхностей (рис23.).
|
Рис.23 |





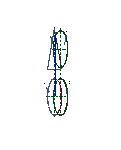
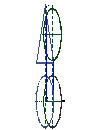
 Рис.21
Рис.21