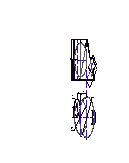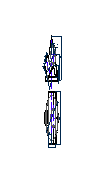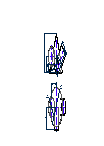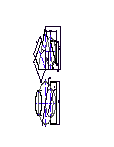3.6. Развертки поверхностей

Развертыванием поверхности называется такое ее преобразование, в результате которого она совмещается с плоскостью. При этом поверхности, полностью совмещаемые с плоскостью (без складок и разрывов), называют развертывающимися, в противном случае неразвертывающимися.

Плоская фигура, полученная в результате развертывания поверхности тела, называется разверткой.

К развертывающимся поверхностям относятся все граненые поверхности, а из линейчатых поверхностей - цилиндрические, конические и с ребром возврата. Остальные линейчатые и все кривые поверхности - неразвертывающиеся.

Под разверткой многогранной поверхности подразумевают плоскую фигуру, составленную из граней этой поверхности, совмещенных с одной плоскостью.

Существуют три способа построения развертки многогранных поверхностей:

1) Способ треугольников (триангуляции);

2) Способ нормального сечения;

3) Способ раскатки.

Способ треугольников (триангуляции)

Этот способ применяется для построения развертки пирамидальных поверхностей. Сущность его: последовательное совмещение всех граней пирамиды (грани представляют собой треугольники) с плоскостью. Построение разверток пирамидальных поверхностей сводится к многократному построению истинных величин треугольников, из которых состоит поверхность, развертываемой пирамиды или которой заменяют развертываемую коническую поверхность.

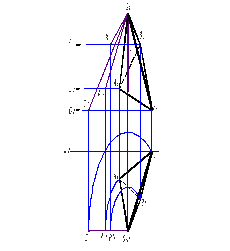
Задача 7. Построить полную развертку поверхности пирамиды.

Шаг 1. По заданным координатам точек строятся проекции поверхности пирамиды.

Шаг 2. Определение длин ребер пирамиды выполнено с помощью вращения вокруг оси i перпендикулярной к горизонтальной плоскости проекций П₁ (рис.50). Путем вращения ребра пирамиды совмещаются с плоскостями, соответственно с Ω, Г, Δ (пример решения на рис. 42).

Натуральная величина основания пирамиды определяется любым известным способом, например – заменой плоскостей проекций (рис. 39).

Рис. 50

Шаг 3. После того как определены длины ребер, приступаем к построению развертки.

На свободном поле чертежа через точку S₀ проводим прямую l. Далее на прямой l откладываем от точки S₀ отрезок длиной S₂ С′₂ получаем точку С₀. Из точки С₀ поводим дугу радиуса R=C₅A₅. а из точки S– дугу радиуса R=S₂А′₂. Пересечение дуг укажет положение вершины А₀. Соединив полученные точки определяем грань пирамиды А₀S₀С₀ (рис.51).

Рис. 51

Аналогично находим точки В₀ и С₀. Соединив точки S₀А₀В₀С₀А₀ получим развертку боковой поверхности пирамиды S₀ А₀ В₀С₀ (рис.52).

Шаг 4. Для получения полной развертки поверхности пирамиды (рис.53) достаточно к какому- либо из звеньев ломаной линии А₀ В₀С₀ А₀ пристроить треугольник основания А₀ В₀С₀ (к А₀С₀).

Рис. 52

Рис. 53

3.7. Контрольные вопросы для подготовки к экзамену

1. Параллельность прямой и плоскости, двух плоскостей?

2. Когда прямая перпендикулярна плоскости на комплексном чертеже?

3. Когда плоскость перпендикулярна плоскости на комплексном чертеже?

4. Сущность метода прямоугольного треугольника?

5. Условие параллельности прямой и плоскости, плоскостей на чертеже.

6. Условие перпендикулярности прямой и плоскости, плоскостей.

7. Какие линии плоскости используются при проведении перпендикуляра к плоскости и почему?

8. Сформулируйте теорему о проецировании прямого угла.

9. Способы преобразования комплексного чертежа.

10. Сущность способа замены плоскостей проекций.

11. Сущность способа вращения вокруг проецирующих прямых?

12. Сущность способа вращения вокруг прямых уровня?

13. Сущность способа плоскопараллельного перемещения?

14. Какие задачи называются метрическими?

15. Как определить длину отрезка и угол его наклона к П1 методом перемены плоскостей проекций. ?

16. Как определить длину отрезка и угол его наклона к П1 методом вращения. ?

17. Как определить длину отрезка и угол его наклона к П2 методом плоскопараллельного перемещении?

18. Как располагается дополнительная плоскость проекций относительно основных плоскостей проекций (П1, П2, П3)?

19. Сколько перемен плоскостей проекций и в какой последовательности необходимо произвести, чтобы определить натуральную величину плоской геометрической фигуры)?

20. Как определить величину отрезка прямой общего положения по ее ортогональным проекциям?

21. Как построить на эпюре Монжа проекции двух прямых, прямой перпендикулярной к плоскости, двух взаимно перпендикулярных плоскостей?

22. Как определить расстояние от точки до плоскости?

23. В каких случаях угловые величины проецируются без искажения?

24. Что является мерой угла между скрещивающимися прямыми?

25. Как построить проекции точки на дополнительную плоскость, перпендикулярную П1?

26. Что называется разверткой поверхности?

27. Какие поверхности относятся к развертывающимся?

28. Сформулируйте основные свойства развертки.

29. В каких случаях при построении развертки используется метод триангуляции?

30. В каких случаях при построении развертки используется способ нормального сечения?

31. В каких случаях при построении развертки используется способ раскатки?

32. Как можно построить развертку усеченной конической поверхности с недоступной вершиной?

33. В чем состоит общий прием решения задачи на построение условной развертки неразвертываемых поверхностей?

Приложение1

Таблица №1

Исходные данные
Вар зад.	A			B				С			D
	x	y	z		x	y	z	x	y	z	x	y	z
1	65	10	20		10	20	0	0	60	60	35	70	5
2	70	0	60		45	50	10	0	20	10	20	50	55
3	70	60	45		40	0	55	0	45	10	65	15	0
4	65	20	0		40	5	55	0	50	5	70	65	55
5	60	60	10		45	15	55	0	5	25	10	45	55
6	60	65	20		45	20	50	5	10	10	70	20	10
7	65	15	0		40	0	55	0	40	20	55	60	50
8	60	65	30		45	10	60	5	10	20	75	15	10
9	75	25	0		30	5	50	10	60	20	60	55	55
10	80	20	10		45	0	70	0	45	40	10	0	15
11	65	20	55		20	5	5	0	50	25	60	55	10
12	75	5	25		35	55	65	0	25	0	65	55	0
13	80	0	40		0	20	70	30	45	0	70	55	65
14	70	10	20		50	45	50	0	25	10	60	55	0
15	65	20	10		10	0	20	0	60	60	35	5	75
16	70	60	0		45	10	50	0	10	20	20	55	50
17	70	45	60		40	55	0	0	10	45	65	0	15
18	65	0	20		40	55	5	0	5	50	70	55	65
Продолжение табл. 1
Вар зад.	A			B				С			D
	x	y	z		x	y	z	x	y	z	x	y	z
19	60	10	60		45	55	15	0	25	5	10	55	45
20	60	20	65		45	50	20	5	10	10	70	10	20
21	65	0	5		40	55	0	0	20	40	55	50	60
22	60	30	65		45	60	10	5	20	10	75	10	15
23	75	25	0		30	50	5	10	20	60	60	55	55
24	80	10	20		45	70	0	0	40	45	10	15	0
25	65	55	20		25	5	5	0	25	50	60	10	55
26	75	25	5		35	65	55	0	0	25	65	0	55
27	80	40	0		0	70	20	30	0	45	70	65	55
28	60	60	10		45	15	55	0	5	25	10	45	55
29	70	10	20		50	45	50	0	25	10	60	55	0
30	65	10	20		10	20	0	0	60	60	35	70	5

Таблица № 2а

Исходные данные
Варианты заданий	A			B			C
	x	y	z	x	y	z	x	y	z
1	130	65	60	15	80	40	80	20	0
2	130	0	60	15	65	45	65	0	0
3	15	60	70	130	60	50	45	10	20
4	30	70	50	110	40	80	85	0	0
5	130	60	25	20	65	75	45	15	10
6	20	15	40	130	0	70	85	65	0
7	105	55	70	10	55	35	55	10	10
8	20	20	0	70	60	60	130	10	0
9	110	60	5	20	25	45	130	0	60
10	130	30	10	50	70	70	20	0	0
11	130	65	60	15	80	40	80	20	0
12	130	0	60	15	65	45	65	0	0
13	15	60	70	130	60	50	45	10	20
14	30	70	50	110	40	80	85	0	0
15	130	60	25	20	65	75	45	15	10
16	20	15	40	130	0	70	85	65	0
17	105	55	70	10	55	35	55	10	10

Продолжение табл. 2а
Варианты заданий	A	B		C			A
	x	y	z	x	y	z	x	y	z
18	20	20	0	70	60	60	130	10	0
19	110	60	5	20	25	45	130	0	60
20	130	30	10	50	70	70	20	0	0
21	130	60	25	20	65	75	45	15	10
22	20	15	40	130	0	70	85	65	0
23	105	55	70	10	55	35	55	10	10
24	20	20	0	70	60	60	130	10	0
25	110	60	5	20	25	45	130	0	60
26	130	30	10	50	70	70	20	0	0
27	130	65	60	15	80	40	80	20	0
28	130	0	60	15	65	45	65	0	0
29	15	60	70	130	60	50	45	10	20
30	30	70	50	110	40	80	85	0	0

Таблица № 2б

Исходные данные
Вар зад.	D			E				F			H
	x	y	z		x	y	z	x	y	z	x	y	z
1	130	20	75		90	80	20	45	65	25	20	?	55
2	110	20	70		110	70	25	55	60	15	2	20	?
3	110	75	20		25	75	20	10	30	55	80	?	70
4	65	0	85		10	40	30	110	60	15	130	30	?
5	115	45	40		100	0	60	10	0	60	85	?	10
6	10	55	70		60	0	10	110	20	20	85	65	?
7	120	25	25		20	25	60	35	70	0	80	?	0
8	35	10	55		110	0	35	95	60	0	10	40	?
9	20	25	30		55	10	10	130	60	35	80	?	80
10	10	10	60		110	10	50	95	60	0	30	60	?
11	130	20	75		90	80	20	45	65	25	20	?	55
12	110	20	70		110	70	25	55	60	15	2	20	?
13	110	75	20		25	75	20	10	30	55	80	?	70
14	65	0	85		10	40	30	110	60	15	130	30	?
15	115	45	40		100	0	60	10	0	60	85	?	10
16	10	55	70		60	0	10	110	20	20	85	65	?
Продолжение табл. 2б
Вар зад.	D			E				F			H
	x	y	z		x		x	y	z	x		x	y
17	120	25	25		20	25	60	35	70	0	80	?	0
18	35	10	55		110	0	35	95	60	0	10	40	?
19	20	25	30		55	10	10	130	60	35	80	?	80
20	10	10	60		110	10	50	95	60	0	30	60	?
21	115	45	40		100	0	60	10	0	60	85	?	10
22	10	55	70		60	0	10	110	20	20	85	65	?
23	120	25	25		20	25	60	35	70	0	80	?	0
24	35	10	55		110	0	35	95	60	0	10	40	?
25	20	25	30		55	10	10	130	60	35	80	?	80
26	10	10	60		110	10	50	95	60	0	30	60	?
27	130	20	75		90	80	20	45	65	25	20	?	55
28	110	20	70		110	70	25	55	60	15	2	20	?
29	110	75	20		25	75	20	10	30	55	80	?	70
30	65	0	85		10	40	30	110	60	15	130	30	?

Таблица № 3

Исходные данные
Вар зад.	A			B			С			S
	x	y	z	x	y	z	x	y	z	x	y	z
1	60	30	5	15	7	25	20	22	50	5	50	40
2	65	30	5	10	8	20	20	20	50	5	40	45
3	68	25	0	15	8	25	30	25	40	5	60	45
4	70	40	0	10	10	30	21	25	50	10	65	35
5	65	30	5	15	7	5	18	20	52	2	50	42
6	70	25	7	12	6	3	45	0	45	5	40	50
7	65	30	5	8	8	25	21	22	50	2	50	40
8	63	35	3	15	6	28	22	23	55	5	52	42
9	68	32	2	13	8	25	50	0	40	10	50	55
10	65	30	5	10	7	23	23	23	50	3	52	40
11	68	32	4	15	8	4	21	25	52	5	53	48
12	64	32	6	15	7	25	40	40	40	2	50	45
13	62	30	5	15	5	30	21	23	48	5	55	40
14	65	40	0	13	0	30	23	20	46	3	48	45
15	70	30	3	15	3	25	21	26	50	3	45	45
16	68	28	4	14	8	20	21	25	50	5	52	42
Продолжение табл. 3
Вар зад.	A			B			С			S
	x	y	z	x	y	z	x	y	z	x	y	z
17	65	30	5	15	6	25	20	35	50	0	50	40
18	60	35	5	10	5	28	18	26	52	2	51	41
19	61	31	2	8	7	26	21	31	50	3	50	42
20	62	0	5	15	7	25	21	25	48	5	50	45
21	64	28	3	14	6	28	25	25	50	5	50	40
22	70	27	4	15	6	25	18	20	48	5	48	48
23	65	8	5	15	7	25	20	24	50	5	50	40
24	65	30	5	15	8	25	10	20	15	5	50	40
25	65	0	5	15	0	25	20	25	50	5	55	45
26	60	30	5	15	7	25	20	22	50	5	50	40
27	65	30	5	10	8	20	20	20	50	5	40	45
28	68	25	0	15	8	25	30	25	40	5	60	45
29	70	40	0	10	10	30	21	25	50		65	35
30	65	30	5	15	8	5	18	50	52	52	50	42

Таблица 3

Вариант 1
Вариант 2

Вариант 3
Вариант 4

Вариант5
Вариант 6

Вариант 7
Вариант 8

Вариант9
Вариант 10

Вариант 11
Вариант 12

Вариант 13
Вариант 14

Вариант 15
Вариант 16
Вариант 17
Вариант 18

Вариант 19
Вариант 20

Вариант 21
Вариант 22

Вариант 23
Вариант 24

Вариант 25
Вариант 26

Вариант 27
Вариант 28

Вариант 29
Вариант 30

Приложение2

Образец 1

Образец 2

Образец 3

Образец 4

Образец 5

Образец 6

Образец 7